Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Pengertian Volume dan Luas Permukaan Bangun Ruang
Volume dan luas permukaan adalah dua konsep penting dalam matematika yang berhubungan dengan bangun ruang. Volume adalah ukuran ruang yang diisi oleh suatu objek, sementara luas permukaan adalah ukuran dari total area permukaan objek.
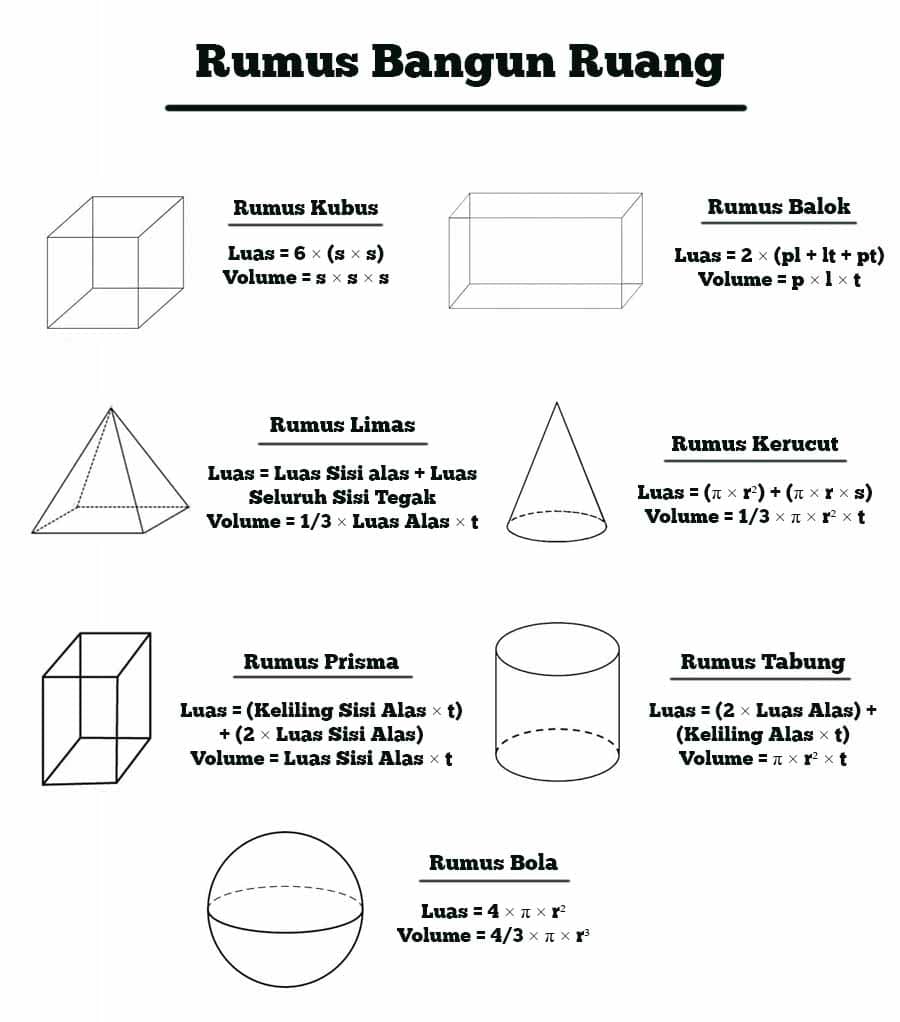
Bangun ruang adalah suatu benda yang memiliki tiga dimensi, yaitu panjang, lebar, dan tinggi. Contoh bangun ruang antara lain kubus, balok, bola, tabung, kerucut, dan prisma.
Volume dan luas permukaan bangun ruang sangat penting dalam berbagai konteks, seperti dalam arsitektur, teknik sipil, dan bidang lainnya. Dalam artikel ini, kita akan membahas lebih detail tentang volume dan luas permukaan bangun ruang.
Volume Bangun Ruang
Volume bangun ruang adalah ukuran ruang yang diisi oleh suatu objek. Hal ini dapat dihitung dengan menggunakan formula matematika tertentu untuk setiap bangun ruang.
1. Kubus
Kubus adalah salah satu bangun ruang yang memiliki bentuk kotak dengan panjang, lebar, dan tinggi yang sama. Volume kubus dapat dihitung dengan rumus:
V = s³
Keterangan:
V = Volume kubus
s = Panjang sisi kubus
Contoh Soal:
Sebuah kubus memiliki panjang sisi 5 cm, berapakah volume yang dihasilkan?
V = s³
V = 5³
V = 125 cm³
2. Balok
Balok adalah bangun ruang yang memiliki bentuk persegi panjang dengan panjang, lebar, dan tinggi yang berbeda. Volume balok dapat dihitung dengan rumus:
V = p x l x t
Keterangan:
V = Volume balok
p = Panjang
l = Lebar
t = Tinggi
Contoh Soal:
Sebuah balok memiliki panjang 4 cm, lebar 3 cm, dan tinggi 2 cm, berapakah volume yang dihasilkan?
V = p x l x t
V = 4 x 3 x 2
V = 24 cm³
3. Bola
Bola adalah bangun ruang yang memiliki bentuk bulat dengan jari-jari r. Volume bola dapat dihitung dengan rumus:
V = 4/3πr³
Keterangan:
V = Volume bola
π = Pi (3,14)
r = Jari-jari bola
Contoh Soal:
Sebuah bola memiliki jari-jari 7 cm, berapakah volume yang dihasilkan?
V = 4/3πr³
V = 4/3 x 3,14 x 7³
V = 1436,76 cm³
4. Tabung
Tabung adalah bangun ruang yang memiliki bentuk silinder dengan jari-jari r dan tinggi t. Volume tabung dapat dihitung dengan rumus:
V = πr²t
Keterangan:
V = Volume tabung
π = Pi (3,14)
r = Jari-jari tabung
t = Tinggi tabung
Contoh Soal:
Sebuah tabung memiliki jari-jari 5 cm dan tinggi 10 cm, berapakah volume yang dihasilkan?
V = πr²t
V = 3,14 x 5² x 10
V = 785 cm³
5. Kerucut
Kerucut adalah bangun ruang yang memiliki bentuk kerucut dengan jari-jari r dan tinggi t. Volume kerucut dapat dihitung dengan rumus:
V = 1/3πr²t
Keterangan:
V = Volume kerucut
π = Pi (3,14)
r = Jari-jari kerucut
t = Tinggi kerucut
Contoh Soal:
Sebuah kerucut memiliki jari-jari 6 cm dan tinggi 8 cm, berapakah volume yang dihasilkan?
V = 1/3πr²t
V = 1/3 x 3,14 x 6² x 8
V = 301,44 cm³
6. Prisma
Prisma adalah bangun ruang yang memiliki bentuk segitiga, persegi, atau lainnya pada bagian atas dan bawahnya dengan sisi-sisi yang sama dan memiliki tinggi yang sama. Volume prisma dapat dihitung dengan rumus:
V = LA x t
Keterangan:
V = Volume prisma
LA = Luas alas
t = Tinggi prisma
Contoh Soal:
Sebuah prisma segitiga memiliki alas 12 cm, tinggi 10 cm, dan tinggi prisma 20 cm, berapakah volume yang dihasilkan?
V = LA x t
V = 1/2 x 12 x 10 x 20
V = 1200 cm³
Luas Permukaan Bangun Ruang
Luas permukaan bangun ruang adalah ukuran dari total area permukaan objek. Hal ini dapat dihitung dengan menggunakan formula matematika tertentu untuk setiap bangun ruang.
1. Kubus
Luas permukaan kubus dapat dihitung dengan rumus:
LP = 6s²
Keterangan:
LP = Luas permukaan kubus
s = Panjang sisi kubus
Contoh Soal:
Sebuah kubus memiliki panjang sisi 5 cm, berapakah luas permukaan yang dihasilkan?
LP = 6s²
LP = 6 x 5²
LP = 150 cm²
2. Balok
Luas permukaan balok dapat dihitung dengan rumus:
LP = 2(pl + pt + lt)
Keterangan:
LP = Luas permukaan balok
p = Panjang
l = Lebar
t = Tinggi
Contoh Soal:
Sebuah balok memiliki panjang 4 cm, lebar 3 cm, dan tinggi 2 cm, berapakah luas permukaan yang dihasilkan?
LP = 2(pl + pt + lt)
LP = 2(4 x 3 + 4 x 2 + 3 x 2)
LP = 52 cm²
3. Bola
Luas permukaan bola dapat dihitung dengan rumus:
LP = 4πr²
Keterangan:
LP = Luas permukaan bola
π = Pi (3,14)
r = Jari-jari bola
Contoh Soal:
Sebuah bola memiliki jari-jari 7 cm, berapakah luas permukaan yang dihasilkan?
LP = 4πr²
LP = 4 x 3,14 x 7²
LP = 615,44 cm²
4. Tabung
Luas permukaan tabung dapat dihitung dengan rumus:
LP = 2πr(t + r)
Keterangan:
LP = Luas permukaan tabung
π = Pi (3,14)
r = Jari-jari tabung
t = Tinggi tabung
Contoh Soal:
Sebuah tabung memiliki jari-jari 5 cm dan tinggi 10 cm, berapakah luas permukaan yang dihasilkan?
LP = 2πr(t + r)
LP = 2 x 3,14 x 5(10 + 5)
LP = 471 cm²
5. Kerucut
Luas permukaan kerucut dapat dihitung dengan rumus:
LP = πr² + πr√(r² + t²)
Keterangan:
LP = Luas permukaan kerucut
π = Pi (3,14)
r = Jari-jari kerucut
t = Tinggi kerucut
Contoh Soal:
Sebuah kerucut memiliki jari-jari 6 cm dan tinggi 8 cm, berapakah luas permukaan yang dihasilkan?
LP = πr² + πr√(r² + t²)
LP = 3,14 x 6² + 3,14 x 6√(6² + 8²)
LP = 244,38 cm²
6. Prisma
Luas permukaan prisma dapat dihitung dengan rumus:
LP = 2LA + (pl + pt + lt)
Keterangan:
LP = Luas permukaan prisma
LA = Luas alas
p = Panjang
l = Lebar
t = Tinggi
Contoh Soal:
Sebuah prisma segitiga memiliki alas 12 cm, tinggi 10 cm, dan tinggi prisma 20 cm, berapakah luas permukaan yang dihasilkan?
LP = 2LA + (pl + pt + lt)
LP = 2(1/2 x 12 x 10) + (12 x 10 + 12 x 20 + 10 x 20)
LP = 680 cm²
Kesimpulan
Volume dan luas permukaan bangun ruang adalah konsep penting dalam matematika yang berhubungan dengan bangun ruang. Volume adalah ukuran ruang yang diisi oleh suatu objek, sementara lu
