Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Pengenalan tentang Volume Bangun Ruang
Volume Bangun Ruang merupakan besaran yang banyak digunakan dalam matematika, khususnya dalam geometri. Volume sendiri memiliki arti sebagai besaran yang menunjukkan ruang yang ditempati oleh suatu benda atau objek. Sementara itu, bangun ruang adalah suatu benda yang memiliki tiga dimensi, yaitu panjang, lebar, dan tinggi.
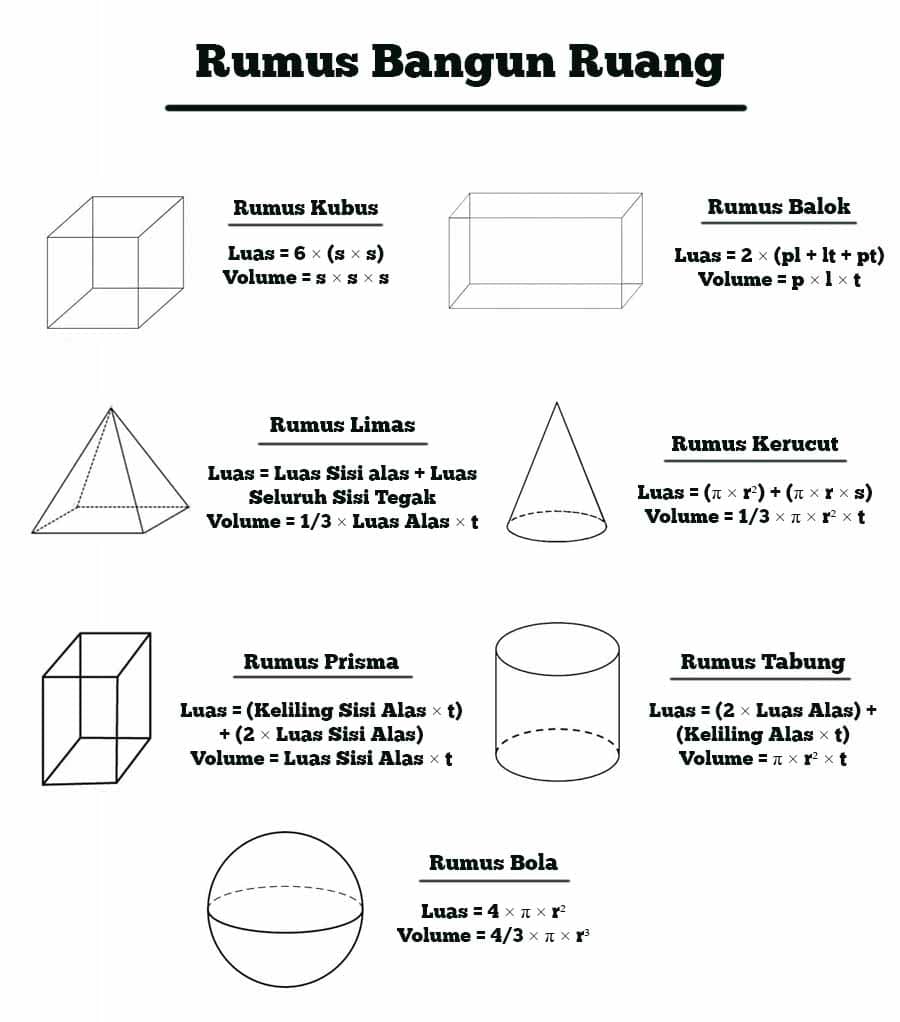
Dalam geometri, terdapat beberapa jenis bangun ruang yang umumnya digunakan untuk menghitung volume. Beberapa di antaranya adalah balok, kubus, limas, prisma, dan tabung. Setiap jenis bangun ruang memiliki rumus yang berbeda-beda untuk menghitung volumenya.
Pada artikel ini, akan dijelaskan mengenai cara menghitung volume dari beberapa jenis bangun ruang. Selain itu, akan dijelaskan juga mengenai pengertian, rumus, dan contoh soal untuk memudahkan pemahaman.
1. Menghitung Volume Balok
Balok adalah bangun ruang yang memiliki tiga pasang sisi yang sama dan saling sejajar. Sisi-sisi tersebut berbentuk persegi atau persegi panjang. Rumus untuk menghitung volume balok adalah sebagai berikut:
V = p x l x t
Keterangan:
V = volume balok
p = panjang balok
l = lebar balok
t = tinggi balok
Contoh Soal:
Sebuah balok memiliki panjang 10 cm, lebar 6 cm, dan tinggi 8 cm. Berapakah volumenya?
Jawab:
V = p x l x t
V = 10 cm x 6 cm x 8 cm
V = 480 cm³
Jadi, volumenya adalah 480 cm³.
2. Menghitung Volume Kubus
Kubus adalah bangun ruang yang memiliki enam sisi yang sama besar dan berbentuk persegi. Setiap sisi pada kubus memiliki panjang yang sama. Rumus untuk menghitung volume kubus adalah sebagai berikut:
V = s³
Keterangan:
V = volume kubus
s = panjang sisi kubus
Contoh Soal:
Sebuah kubus memiliki panjang sisi 5 cm. Berapakah volumenya?
Jawab:
V = s³
V = 5 cm x 5 cm x 5 cm
V = 125 cm³
Jadi, volumenya adalah 125 cm³.
3. Menghitung Volume Limas
Limas adalah bangun ruang yang memiliki alas berbentuk segi-n dan lima sisi yang sama besar. Sisi-sisi pada limas tidak sejajar dan memiliki tinggi yang berbeda-beda. Rumus untuk menghitung volume limas adalah sebagai berikut:
V = 1/3 x L x t
Keterangan:
V = volume limas
L = luas alas limas
t = tinggi limas
Contoh Soal:
Sebuah limas memiliki luas alas 30 cm² dan tinggi 10 cm. Berapakah volumenya?
Jawab:
V = 1/3 x L x t
V = 1/3 x 30 cm² x 10 cm
V = 100 cm³
Jadi, volumenya adalah 100 cm³.
4. Menghitung Volume Prisma
Prisma adalah bangun ruang yang memiliki dua alas berbentuk segi-n dan sisi-sisi yang berbentuk persegi atau persegi panjang. Alas-alas pada prisma sejajar dan memiliki luas yang sama. Rumus untuk menghitung volume prisma adalah sebagai berikut:
V = L x t
Keterangan:
V = volume prisma
L = luas alas prisma
t = tinggi prisma
Contoh Soal:
Sebuah prisma memiliki luas alas 20 cm² dan tinggi 15 cm. Berapakah volumenya?
Jawab:
V = L x t
V = 20 cm² x 15 cm
V = 300 cm³
Jadi, volumenya adalah 300 cm³.
5. Menghitung Volume Tabung
Tabung adalah bangun ruang yang memiliki dua lingkaran sebagai alasnya dan sisi-sisinya berbentuk silinder. Jarak antara dua lingkaran pada tabung disebut sebagai tinggi tabung. Rumus untuk menghitung volume tabung adalah sebagai berikut:
V = π x r² x t
Keterangan:
V = volume tabung
π = 22/7 atau 3,14
r = jari-jari lingkaran (setengah dari panjang diameter)
t = tinggi tabung
Contoh Soal:
Sebuah tabung memiliki jari-jari 7 cm dan tinggi 10 cm. Berapakah volumenya?
Jawab:
V = π x r² x t
V = 22/7 x 7 cm x 7 cm x 10 cm
V = 1540/7 cm³
V = 220 cm³
Jadi, volumenya adalah 220 cm³.
Kesimpulan
Volume Bangun Ruang merupakan besaran yang banyak digunakan dalam matematika, khususnya dalam geometri. Terdapat beberapa jenis bangun ruang yang umumnya digunakan untuk menghitung volume, yaitu balok, kubus, limas, prisma, dan tabung. Setiap jenis bangun ruang memiliki rumus yang berbeda-beda untuk menghitung volumenya.
Dalam menghitung volume bangun ruang, diperlukan pemahaman yang baik mengenai rumus dan cara-cara yang tepat untuk mengaplikasikannya. Dengan menguasai cara-cara tersebut, diharapkan dapat mempermudah dalam menyelesaikan soal-soal yang berkaitan dengan volume bangun ruang.
