Daftar Isi
Pengenalan Volume Bangun Datar
Volume bangun datar merupakan besaran fisika yang mengukur ruang atau isi dari sebuah bangun datar. Bangun datar adalah bangun geometri yang memiliki dua dimensi, yaitu panjang dan lebar. Beberapa contoh bangun datar antara lain persegi, persegi panjang, segitiga, trapesium, jajar genjang, dan lain sebagainya. Setiap bangun datar memiliki rumus yang berbeda dalam menghitung volumenya.
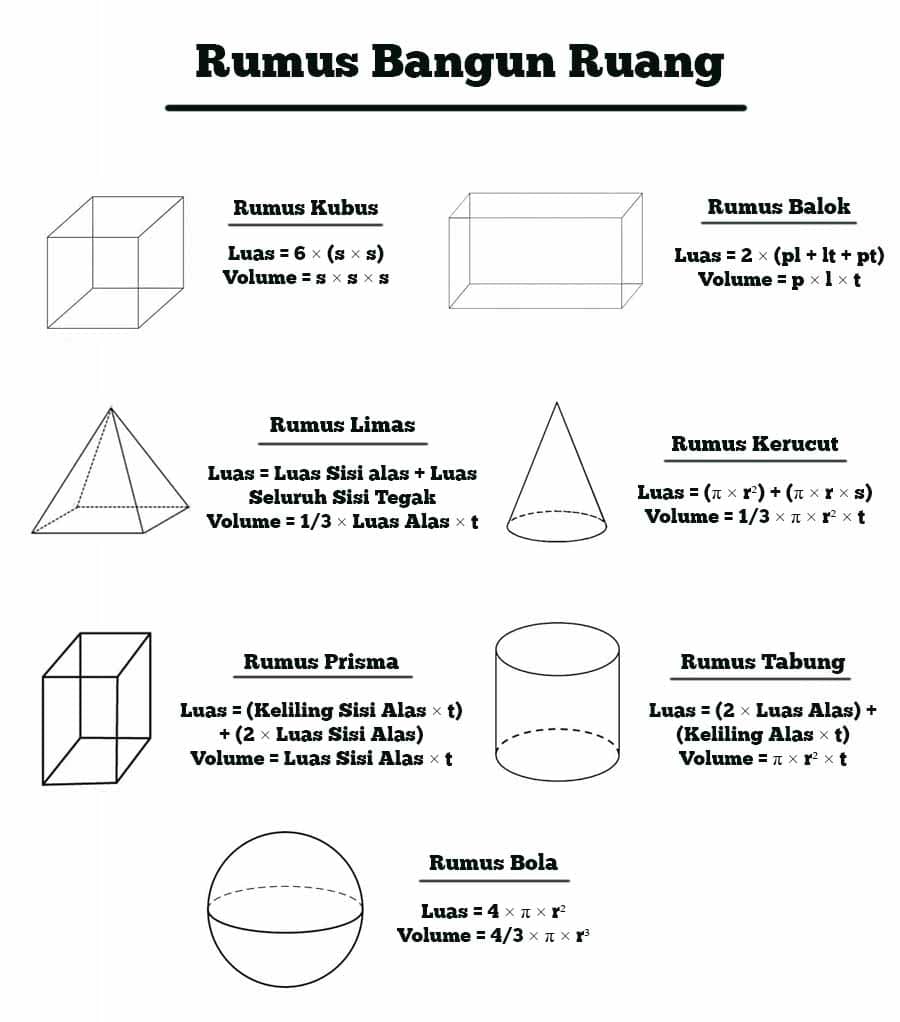
Dalam matematika, volume dapat dihitung dengan rumus tertentu berdasarkan dimensi dan bentuk bangunan yang diukur. Pada volume bangun datar, rumus yang digunakan akan berbeda-beda tergantung pada jenis bangun datar yang diukur. Oleh karena itu, penting bagi kita untuk mengetahui rumus volume bangun datar beserta contohnya agar dapat menghitung dengan tepat.
Berikut ini akan dijelaskan cara menghitung volume untuk berbagai macam bangun datar:
1. Volume Kubus
Kubus adalah bangun datar tiga dimensi yang memiliki enam sisi yang sama panjang. Sisi-sisi kubus tersebut membentuk enam persegi dengan sudut-sudut yang siku-siku. Untuk menghitung volume kubus, kita dapat menggunakan rumus sederhana yaitu panjang sisi pangkat tiga.
Contoh:
Sebuah kubus memiliki panjang sisi 5 cm. Berapa volume kubus tersebut?
Penyelesaian:
V = sisi x sisi x sisi
V = 5cm x 5cm x 5cm
V = 125 cm³
Jadi, volume kubus tersebut adalah 125 cm³.
2. Volume Balok
Balok adalah bangun datar tiga dimensi yang memiliki tiga pasang sisi yang sama panjang. Balok memiliki enam sisi, yaitu dua pasang sisi yang sama panjang dan satu pasang sisi yang sama panjang dengan ukuran yang berbeda. Untuk menghitung volume balok, kita dapat menggunakan rumus panjang x lebar x tinggi.
Contoh:
Sebuah balok memiliki panjang 12 cm, lebar 8 cm, dan tinggi 6 cm. Berapa volume balok tersebut?
Penyelesaian:
V = panjang x lebar x tinggi
V = 12cm x 8cm x 6cm
V = 576 cm³
Jadi, volume balok tersebut adalah 576 cm³.
3. Volume Prisma Segitiga
Prisma segitiga adalah bangun datar tiga dimensi yang memiliki alas berbentuk segitiga dan dua pasang sisi yang sejajar. Prisma segitiga memiliki lima sisi, yaitu tiga sisi segitiga dan dua sisi persegi panjang. Untuk menghitung volume prisma segitiga, kita dapat menggunakan rumus 1/2 x alas x tinggi segitiga x tinggi prisma.
Contoh:
Sebuah prisma segitiga memiliki alas segitiga dengan ukuran 6 cm dan tinggi segitiga 4 cm. Tinggi prisma segitiga tersebut adalah 8 cm. Berapa volume prisma segitiga tersebut?
Penyelesaian:
V = 1/2 x alas x tinggi segitiga x tinggi prisma
V = 1/2 x 6cm x 4cm x 8cm
V = 96 cm³
Jadi, volume prisma segitiga tersebut adalah 96 cm³.
4. Volume Limas Segitiga
Limas segitiga adalah bangun datar tiga dimensi yang memiliki alas berbentuk segitiga dan tiga sisi segitiga yang sama panjang. Limas segitiga memiliki lima sisi, yaitu tiga sisi segitiga dan dua sisi sama kaki. Untuk menghitung volume limas segitiga, kita dapat menggunakan rumus 1/3 x luas alas x tinggi.
Contoh:
Sebuah limas segitiga memiliki alas segitiga dengan ukuran 8 cm dan tinggi segitiga 6 cm. Tinggi limas segitiga tersebut adalah 10 cm. Berapa volume limas segitiga tersebut?
Penyelesaian:
V = 1/3 x luas alas x tinggi
V = 1/3 x 1/2 x alas x tinggi x tinggi
V = 1/3 x 1/2 x 8cm x 6cm x 10cm
V = 80 cm³
Jadi, volume limas segitiga tersebut adalah 80 cm³.
5. Volume Tabung
Tabung adalah bangun datar tiga dimensi yang terdiri dari dua lingkaran yang sama besar pada bagian atas dan bawahnya dan sebuah selimut yang berbentuk silinder. Untuk menghitung volume tabung, kita dapat menggunakan rumus π x r² x tinggi.
Contoh:
Sebuah tabung memiliki panjang jari-jari 5 cm dan tinggi 10 cm. Berapa volume tabung tersebut?
Penyelesaian:
V = π x r² x tinggi
V = 22/7 x 5cm x 5cm x 10cm
V = 785,7 cm³
Jadi, volume tabung tersebut adalah 785,7 cm³.
6. Volume Kerucut
Kerucut adalah bangun datar tiga dimensi yang terdiri dari lingkaran pada bagian alasnya dan sebuah selimut yang berbentuk kerucut. Untuk menghitung volume kerucut, kita dapat menggunakan rumus 1/3 x π x r² x tinggi.
Contoh:
Sebuah kerucut memiliki panjang jari-jari 7 cm dan tinggi 12 cm. Berapa volume kerucut tersebut?
Penyelesaian:
V = 1/3 x π x r² x tinggi
V = 1/3 x 22/7 x 7cm x 7cm x 12cm
V = 539,4 cm³
Jadi, volume kerucut tersebut adalah 539,4 cm³.
7. Volume Bola
Bola adalah bangun datar tiga dimensi yang terdiri dari semua titik yang sama jaraknya dari pusatnya. Untuk menghitung volume bola, kita dapat menggunakan rumus 4/3 x π x r³.
Contoh:
Sebuah bola memiliki panjang jari-jari 10 cm. Berapa volume bola tersebut?
Penyelesaian:
V = 4/3 x π x r³
V = 4/3 x 22/7 x 10cm x 10cm x 10cm
V = 4.188,8 cm³
Jadi, volume bola tersebut adalah 4.188,8 cm³.
Kesimpulan
Volume bangun datar menjadi hal penting dalam pengukuran ruang atau isi dari sebuah bangun datar. Setiap bangun datar memiliki rumus yang berbeda dalam menghitung volumenya. Oleh karena itu, penting bagi kita untuk mengetahui rumus volume bangun datar beserta contohnya agar dapat menghitung dengan tepat. Berbagai macam bangun datar yang umum digunakan dalam penghitungan volume antara lain kubus, balok, prisma segitiga, limas segitiga, tabung, kerucut, dan bola.
 Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
