Belajar Mudah Menghitung Volume Tabung Kelas 6 SD Dengan Contoh Soal Dan Jawaban

Pengenalan

Soal volume tabung adalah salah satu materi yang diajarkan dalam matematika kelas 6 SD. Volume tabung merupakan besaran tiga dimensi yang terdiri dari tinggi dan luas alas. Dalam pembahasan ini, kita akan membahas tentang soal volume tabung untuk kelas 6 SD.

Definisi Volume Tabung

Volume tabung adalah besaran tiga dimensi yang mengukur kapasitas suatu ruang yang berbentuk silinder atau tabung. Volume tabung dihitung dengan rumus V = πr²t, di mana r adalah jari-jari tabung dan t adalah tinggi tabung.

Cara Menghitung Volume Tabung

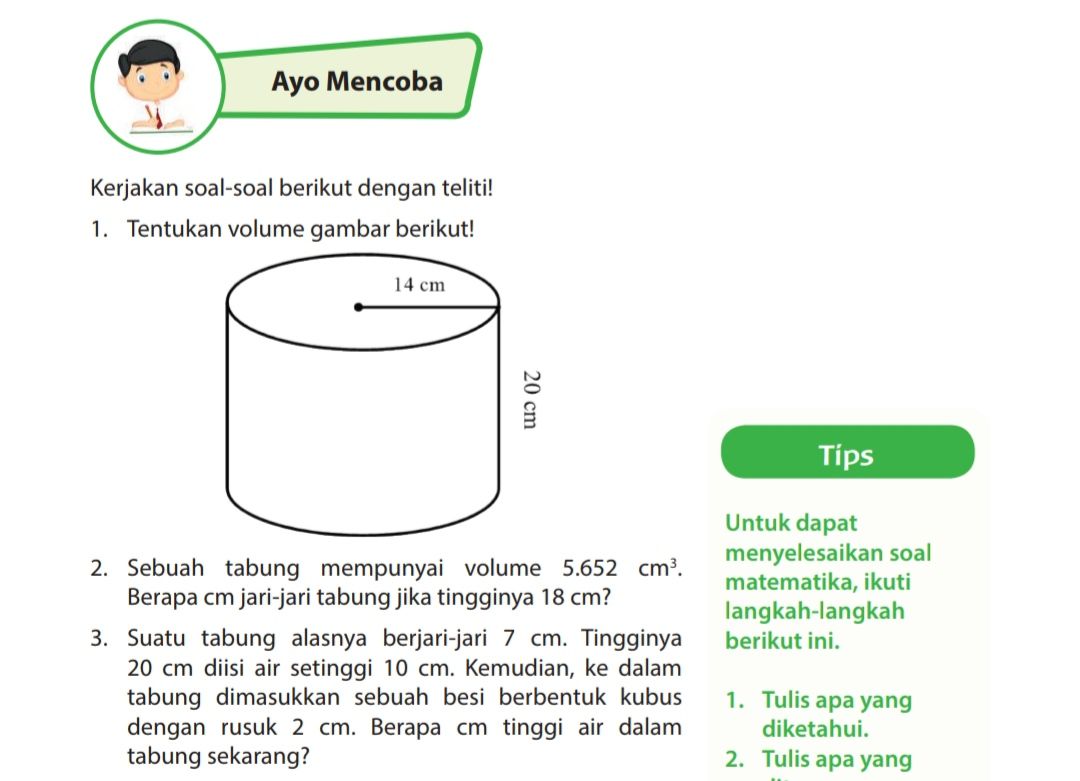
Untuk menghitung volume tabung, ada beberapa langkah yang perlu dilakukan, yaitu:

1. Tentukan jari-jari tabung (r) dan tinggi tabung (t).
2. Hitung luas alas tabung dengan rumus L = πr².
3. Kalikan luas alas tabung dengan tinggi tabung, V = L x t atau V = πr²t.

Contoh:

Sebuah tabung memiliki jari-jari 7 cm dan tinggi 10 cm. Berapa volume tabung tersebut?

Pertama-tama, tentukan jari-jari dan tinggi tabung:

r = 7 cm
t = 10 cm

Selanjutnya, hitung luas alas tabung:

L = πr²
L = π x 7²
L = π x 49
L = 153,94 cm²

Terakhir, hitung volume tabung:

V = L x t
V = 153,94 x 10
V = 1539,4 cm³

Jadi, volume tabung tersebut adalah 1539,4 cm³.

Soal Volume Tabung

Berikut ini adalah beberapa soal volume tabung untuk kelas 6 SD:

1. Sebuah tabung memiliki jari-jari 5 cm dan tinggi 12 cm. Berapa volume tabung tersebut?

Penyelesaian:

r = 5 cm
t = 12 cm

L = πr²
L = π x 5²
L = π x 25
L = 78,54 cm²

V = L x t
V = 78,54 x 12
V = 942,48 cm³

Jadi, volume tabung tersebut adalah 942,48 cm³.

2. Sebuah tabung memiliki volume 150 cm³ dan tinggi 9 cm. Hitunglah jari-jari tabung tersebut!

Penyelesaian:

V = 150 cm³
t = 9 cm

V = πr²t
150 = πr² x 9
150 = 9πr²
r² = 150/9π
r = √(150/9π)
r = 1,9 cm

Jadi, jari-jari tabung tersebut adalah 1,9 cm.

3. Sebuah tabung memiliki jari-jari 6 cm dan tinggi 20 cm. Berapa luas permukaan tabung tersebut?

Penyelesaian:

r = 6 cm
t = 20 cm

L = πr²
L = π x 6²
L = π x 36
L = 113,10 cm²

Lpermukaan = 2πr(t + r)
Lpermukaan = 2π x 6(20 + 6)
Lpermukaan = 2π x 6 x 26
Lpermukaan = 979,80 cm²

Jadi, luas permukaan tabung tersebut adalah 979,80 cm².

4. Sebuah tabung memiliki tinggi 18 cm dan luas permukaan 452,40 cm². Hitunglah jari-jari tabung tersebut!

Penyelesaian:

t = 18 cm
Lpermukaan = 452,40 cm²

Lpermukaan = 2πr(t + r)
452,40 = 2πr(18 + r)
452,40 = 36πr + 2πr²
2πr² + 36πr – 452,40 = 0

Dengan menggunakan rumus abc, diperoleh:

a = 2π = 6,28
b = 36π = 113,10
c = -452,40

r = (-b ± √(b² – 4ac))/2a
r = (-113,10 ± √(113,10² – 4 x 6,28 x (-452,40)))/2 x 6,28
r = (-113,10 ± 27,40)/12,56

r = 6,03 cm atau r = -9,48 cm

Jadi, jari-jari tabung tersebut adalah 6,03 cm.

Kesimpulan

Volume tabung adalah besaran tiga dimensi yang terdiri dari tinggi dan luas alas. Untuk menghitung volume tabung, kita perlu menentukan jari-jari dan tinggi tabung, serta menghitung luas alas tabung dengan rumus L = πr². Volume tabung dihitung dengan rumus V = L x t atau V = πr²t. Ada beberapa soal volume tabung yang dapat dijadikan latihan untuk kelas 6 SD. Dalam menyelesaikan soal, kita perlu memahami rumus-rumus yang berkaitan dengan volume tabung dan melakukan perhitungan dengan teliti.