Segitiga Sama Siku Siku

Segitiga sama siku siku adalah salah satu jenis segitiga yang memiliki dua sisi yang sama panjang dan satu sudut yang besarnya 90 derajat. Segitiga ini cukup sering digunakan dalam matematika dan memiliki banyak aplikasi dalam kehidupan sehari-hari. Dalam artikel ini, akan dibahas tentang pengertian, sifat, rumus, cara menghitung luas dan keliling, serta contoh soal segitiga sama siku siku.

Pengertian Segitiga Sama Siku Siku

Segitiga sama siku siku adalah segitiga yang memiliki salah satu sudutnya sama dengan 90 derajat dan dua sisinya sama panjang. Sudut yang sama dengan 90 derajat disebut sudut siku-siku. Segitiga sama siku siku sering disebut juga dengan segitiga siku-siku atau segitiga pythagoras.

Sifat Segitiga Sama Siku Siku

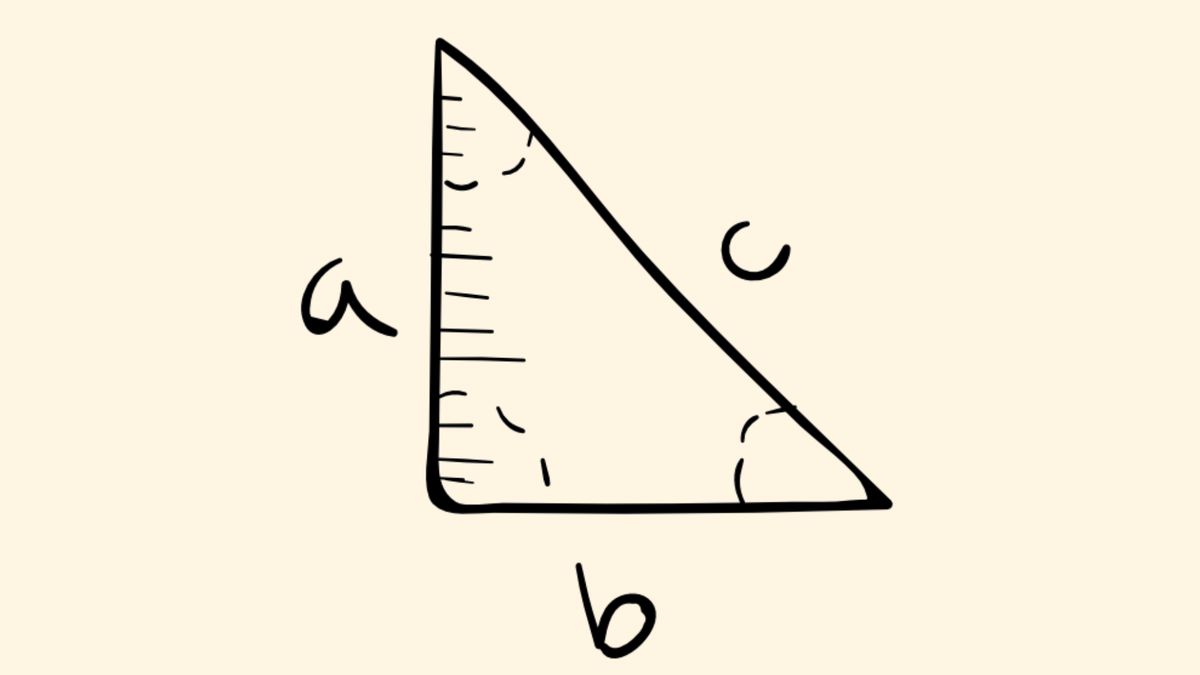
Segitiga sama siku siku memiliki beberapa sifat yang unik, antara lain:

1. Sudut siku-siku
Segitiga sama siku siku memiliki satu sudut yang besarnya 90 derajat. Sudut ini disebut sudut siku-siku.

2. Sisi sama panjang
Segitiga sama siku siku memiliki dua sisi yang sama panjang. Kedua sisi ini selalu bersebrangan dengan sudut siku-siku.

3. Sisi miring
Sisi yang bersebrangan dengan sudut siku-siku disebut sisi miring. Sisi ini selalu lebih panjang dari dua sisi yang lain.

4. Teorema Pythagoras
Segitiga sama siku siku memenuhi teorema Pythagoras, yaitu kuadrat dari sisi miring sama dengan jumlah kuadrat dari dua sisi yang lain. Rumusnya adalah a^2 + b^2 = c^2.

Rumus Segitiga Sama Siku Siku

1. Rumus luas segitiga sama siku siku
Luas segitiga sama siku siku dapat dihitung dengan cara membagi jumlah hasil kali kedua sisi yang sama panjang dengan angka 2. Rumusnya adalah:

L = a × b / 2

Contoh:
Diketahui segitiga sama siku siku dengan panjang sisi 5 cm dan 5 cm. Maka, luas segitiga tersebut adalah:

L = 5 cm × 5 cm / 2
L = 12,5 cm^2

Jadi, luas segitiga tersebut adalah 12,5 cm^2.

2. Rumus keliling segitiga sama siku siku
Keliling segitiga sama siku siku dapat dihitung dengan cara menjumlahkan ketiga sisinya. Rumusnya adalah:

K = a + b + c

Contoh:
Diketahui segitiga sama siku siku dengan panjang sisi 5 cm, 5 cm, dan 7,07 cm. Maka, keliling segitiga tersebut adalah:

K = 5 cm + 5 cm + 7,07 cm
K = 17,07 cm

Jadi, keliling segitiga tersebut adalah 17,07 cm.

Cara Menghitung Luas dan Keliling Segitiga Sama Siku Siku

1. Cara menghitung luas segitiga sama siku siku
Untuk menghitung luas segitiga sama siku siku, dapat dilakukan dengan cara membagi jumlah hasil kali kedua sisi yang sama panjang dengan angka 2. Berikut adalah langkah-langkahnya:

a. Ketahui panjang sisi yang sama panjang.
b. Hitung luas dengan rumus L = a × b / 2.

Contoh:
Diketahui segitiga sama siku siku dengan panjang sisi 5 cm dan 5 cm. Maka, langkah-langkah menghitung luas segitiga tersebut adalah:

a. Panjang sisi yang sama panjang adalah 5 cm.
b. Hitung luas dengan rumus L = a × b / 2
L = 5 cm × 5 cm / 2
L = 12,5 cm^2

Jadi, luas segitiga sama siku siku dengan panjang sisi 5 cm dan 5 cm adalah 12,5 cm^2.

2. Cara menghitung keliling segitiga sama siku siku
Untuk menghitung keliling segitiga sama siku siku, dapat dilakukan dengan cara menjumlahkan ketiga sisinya. Berikut adalah langkah-langkahnya:

a. Ketahui panjang ketiga sisinya.
b. Hitung keliling dengan rumus K = a + b + c.

Contoh:
Diketahui segitiga sama siku siku dengan panjang sisi 5 cm, 5 cm, dan 7,07 cm. Maka, langkah-langkah menghitung keliling segitiga tersebut adalah:

a. Panjang ketiga sisinya adalah 5 cm, 5 cm, dan 7,07 cm.
b. Hitung keliling dengan rumus K = a + b + c
K = 5 cm + 5 cm + 7,07 cm
K = 17,07 cm

Jadi, keliling segitiga sama siku siku dengan panjang sisi 5 cm, 5 cm, dan 7,07 cm adalah 17,07 cm.

Contoh Soal Segitiga Sama Siku Siku

Contoh soal 1:
Diketahui segitiga sama siku siku dengan panjang sisi 6 cm dan 6 cm. Hitunglah luas dan keliling segitiga tersebut!

Penyelesaian:
Luas segitiga = a × b / 2 = 6 cm × 6 cm / 2 = 18 cm^2
Keliling segitiga = a + b + c = 6 cm + 6 cm + 8,49 cm = 20,49 cm

Jadi, luas segitiga sama siku siku tersebut adalah 18 cm^2 dan kelilingnya adalah 20,49 cm.

Contoh soal 2:
Sebuah papan segitiga sama siku siku memiliki sisi miring sepanjang 10 cm. Hitunglah panjang kedua sisinya jika luasnya adalah 30 cm^2!

Penyelesaian:
Luas segitiga = a × b / 2 = 30 cm^2
Sisi miring (c) = 10 cm
Maka, a^2 + b^2 = c^2
a^2 + b^2 = 10^2
a^2 + b^2 = 100
a × b = 60

Dari persamaan di atas, dapat dicari nilai a dan b dengan mengganti salah satu variabel dengan rumus a × b = 60. Misalnya, di sini kita akan mencari nilai a dengan mengganti b dengan rumus tersebut.

a × b = 60
a × (60 / a) = 60
a^2 = 60
a = √60 = 7,75 cm

Maka, b = 60 / 7,75 = 7,74 cm

Jadi, kedua sisinya adalah 7,75 cm dan 7,74 cm.

Contoh soal 3:
Diketahui segitiga sama siku siku dengan panjang sisi 3 cm, 4 cm, dan 5 cm. Hitunglah luas dan keliling segitiga tersebut!

Penyelesaian:
Luas segitiga = a × b / 2 = 3 cm × 4 cm / 2 = 6 cm^2
Keliling segitiga = a + b + c = 3 cm + 4 cm + 5 cm = 12 cm

Jadi, luas segitiga sama siku siku tersebut adalah 6 cm^2 dan kelilingnya adalah 12 cm.

Kesimpulan

Segitiga sama siku siku adalah segitiga yang memiliki salah satu sudutnya sama dengan 90 derajat dan dua sisinya sama panjang. Sisi yang bersebrangan dengan sudut siku-siku disebut sisi miring. Segitiga sama siku siku memenuhi teorema Pythagoras, yaitu kuadrat dari sisi miring sama dengan jumlah kuadrat dari dua sisi yang lain. Luas segitiga sama siku siku dapat dihitung dengan cara membagi jumlah hasil kali kedua sisi yang sama panjang dengan angka 2, sedangkan kelilingnya dapat dihitung dengan cara menjumlahkan ketiga sisinya. Segitiga sama siku siku sering digunakan dalam kehidupan sehari-hari, seperti dalam konstruksi bangunan dan