Rumus Volume Dan Luas Permukaan Bangun Ruang

Bangun ruang adalah benda atau objek tiga dimensi yang memiliki luas permukaan dan volume. Ada berbagai macam bangun ruang seperti kubus, balok, bola, tabung, kerucut, dan prisma. Setiap bangun ruang memiliki rumus volume dan luas permukaan yang berbeda-beda. Dalam artikel ini, kita akan membahas tentang rumus volume dan luas permukaan bangun ruang beserta contohnya.

Bangun Ruang Kubus

Kubus adalah bangun ruang yang memiliki enam sisi yang sama besar dan bentuknya merupakan persegi. Setiap sisi yang bersebrangan memiliki ukuran yang sama. Untuk mencari rumus volume dan luas permukaan kubus, simak penjelasan di bawah ini.

Rumus Volume Kubus

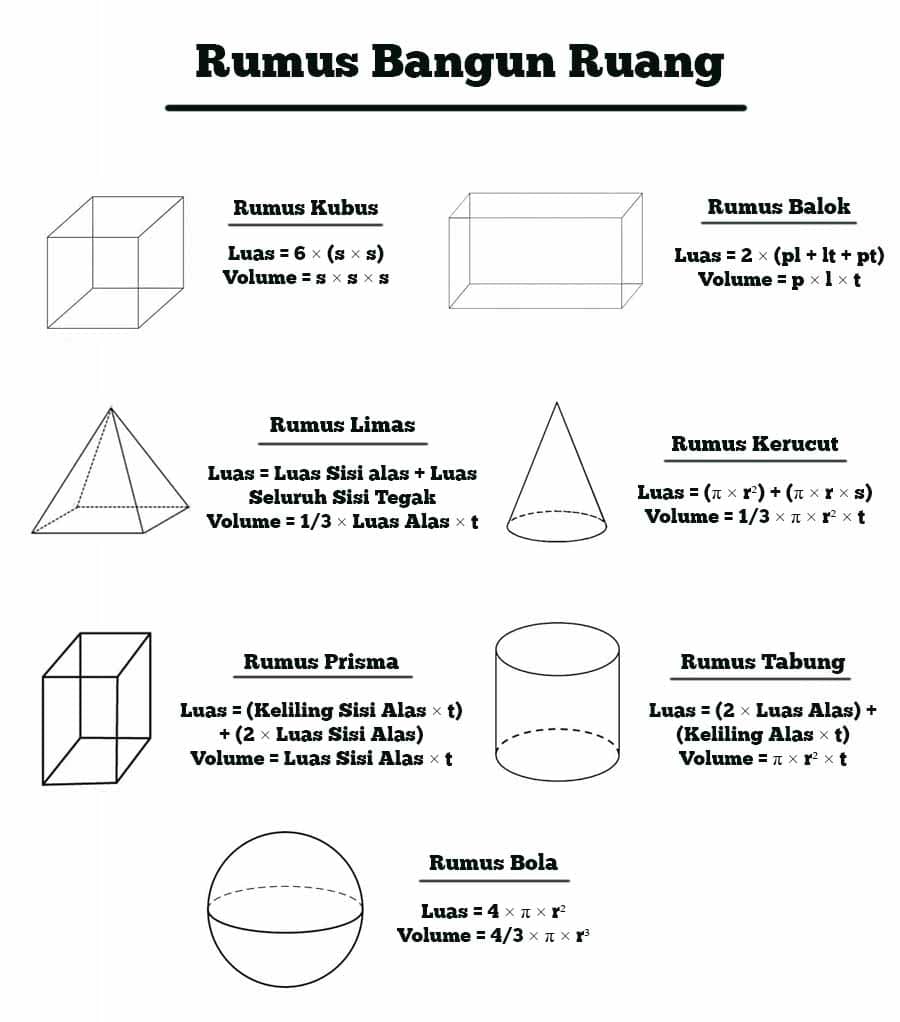
Rumus volume kubus adalah panjang sisi pangkat tiga atau V = s^3.

Contoh Soal:

Sebuah kubus memiliki panjang sisi sebesar 5 cm. Tentukan volume kubus tersebut.

Penyelesaian:

V = s^3
V = 5^3
V = 125 cm³

Jadi, volume kubus tersebut adalah 125 cm³.

Rumus Luas Permukaan Kubus

Rumus luas permukaan kubus adalah enam kali panjang sisi pangkat dua atau LP = 6s^2.

Contoh Soal:

Sebuah kubus memiliki panjang sisi sebesar 4 cm. Tentukan luas permukaan kubus tersebut.

Penyelesaian:

LP = 6s^2
LP = 6 x 4^2
LP = 96 cm²

Jadi, luas permukaan kubus tersebut adalah 96 cm².

Bangun Ruang Balok

Balok adalah bangun ruang tiga dimensi yang memiliki enam sisi. Dua sisi berupa persegi panjang dan empat sisinya berupa persegi. Setiap sisi yang bersebrangan memiliki ukuran yang sama. Untuk mencari rumus volume dan luas permukaan balok, simak penjelasan di bawah ini.

Rumus Volume Balok

Rumus volume balok adalah panjang x lebar x tinggi atau V = p x l x t.

Contoh Soal:

Sebuah balok memiliki panjang 6 cm, lebar 4 cm, dan tinggi 3 cm. Tentukan volume balok tersebut.

Penyelesaian:

V = p x l x t
V = 6 x 4 x 3
V = 72 cm³

Jadi, volume balok tersebut adalah 72 cm³.

Rumus Luas Permukaan Balok

Rumus luas permukaan balok adalah dua kali (panjang x lebar + panjang x tinggi + lebar x tinggi) atau LP = 2pl + 2pt + 2lt.

Contoh Soal:

Sebuah balok memiliki panjang 6 cm, lebar 4 cm, dan tinggi 3 cm. Tentukan luas permukaan balok tersebut.

Penyelesaian:

LP = 2pl + 2pt + 2lt
LP = 2(6 x 4) + 2(6 x 3) + 2(4 x 3)
LP = 120 cm²

Jadi, luas permukaan balok tersebut adalah 120 cm².

Bangun Ruang Bola

Bola adalah bangun ruang yang bentuknya bulat sempurna. Bola tidak memiliki sisi, namun memiliki radius dan diameter. Untuk mencari rumus volume dan luas permukaan bola, simak penjelasan di bawah ini.

Rumus Volume Bola

Rumus volume bola adalah 4/3 kali phi (22/7 atau 3,14) kali radius pangkat tiga atau V = 4/3 x phi x r^3.

Contoh Soal:

Sebuah bola memiliki radius sebesar 7 cm. Tentukan volume bola tersebut.

Penyelesaian:

V = 4/3 x phi x r^3
V = 4/3 x 22/7 x 7^3
V = 1437,33 cm³

Jadi, volume bola tersebut adalah 1437,33 cm³.

Rumus Luas Permukaan Bola

Rumus luas permukaan bola adalah empat kali phi (22/7 atau 3,14) kali radius pangkat dua atau LP = 4 x phi x r^2.

Contoh Soal:

Sebuah bola memiliki radius sebesar 7 cm. Tentukan luas permukaan bola tersebut.

Penyelesaian:

LP = 4 x phi x r^2
LP = 4 x 22/7 x 7^2
LP = 615,44 cm²

Jadi, luas permukaan bola tersebut adalah 615,44 cm².

Bangun Ruang Tabung

Tabung adalah bangun ruang yang terdiri dari dua lingkaran yang sejajar dan sisi lengkung yang menghubungkan kedua lingkaran tersebut. Untuk mencari rumus volume dan luas permukaan tabung, simak penjelasan di bawah ini.

Rumus Volume Tabung

Rumus volume tabung adalah phi (22/7 atau 3,14) kali radius pangkat dua kali tinggi atau V = phi x r^2 x t.

Contoh Soal:

Sebuah tabung memiliki radius sebesar 5 cm dan tinggi 10 cm. Tentukan volume tabung tersebut.

Penyelesaian:

V = phi x r^2 x t
V = 22/7 x 5^2 x 10
V = 785,71 cm³

Jadi, volume tabung tersebut adalah 785,71 cm³.

Rumus Luas Permukaan Tabung

Rumus luas permukaan tabung adalah dua kali phi (22/7 atau 3,14) kali radius kali tinggi ditambah dua kali phi kali radius pangkat dua atau LP = 2 x phi x r x t + 2 x phi x r^2.

Contoh Soal:

Sebuah tabung memiliki radius sebesar 5 cm dan tinggi 10 cm. Tentukan luas permukaan tabung tersebut.

Penyelesaian:

LP = 2 x phi x r x t + 2 x phi x r^2
LP = 2 x 22/7 x 5 x 10 + 2 x 22/7 x 5^2
LP = 471,43 cm²

Jadi, luas permukaan tabung tersebut adalah 471,43 cm².

Bangun Ruang Kerucut

Kerucut adalah bangun ruang yang terdiri dari satu lingkaran dan satu sisi membentuk kerucut. Untuk mencari rumus volume dan luas permukaan kerucut, simak penjelasan di bawah ini.

Rumus Volume Kerucut

Rumus volume kerucut adalah 1/3 kali phi (22/7 atau 3,14) kali radius pangkat dua kali tinggi atau V = 1/3 x phi x r^2 x t.

Contoh Soal:

Sebuah kerucut memiliki radius sebesar 8 cm dan tinggi 12 cm. Tentukan volume kerucut tersebut.

Penyelesaian:

V = 1/3 x phi x r^2 x t
V = 1/3 x 22/7 x 8^2 x 12
V = 804,29 cm³

Jadi, volume kerucut tersebut adalah 804,29 cm³.

Rumus Luas Permukaan Kerucut

Rumus luas permukaan kerucut adalah phi (22/7 atau 3,14) kali radius kali garis pelukis ditambah phi kali radius pangkat dua atau LP = phi x r x l + phi x r^2.

Contoh Soal:

Sebuah kerucut memiliki radius sebesar 8 cm dan garis pelukis 17 cm. Tentukan luas permukaan kerucut tersebut.

Penyelesaian:

LP = phi x r x l + phi x r^2
LP = 22/7 x 8 x 17 + 22/7 x 8^2
LP = 385,71 cm²

Jadi, luas permukaan kerucut tersebut adalah 385,71 cm².

Bangun Ruang Prisma

Prisma adalah bangun ruang tiga dimensi yang memiliki dua sisi segi-n dengan bentuk yang sama dan sisi-sisi tegaknya berbentuk persegi atau