Rumus Luas dan Volume Bangun Ruang
Bangun ruang adalah benda yang memiliki tiga dimensi yaitu panjang, lebar, dan tinggi. Bangun ruang memiliki luas permukaan dan volume yang dapat dihitung menggunakan rumus matematika tertentu. Dalam artikel ini, kita akan membahas rumus luas dan volume untuk beberapa jenis bangun ruang, beserta contoh perhitungannya.
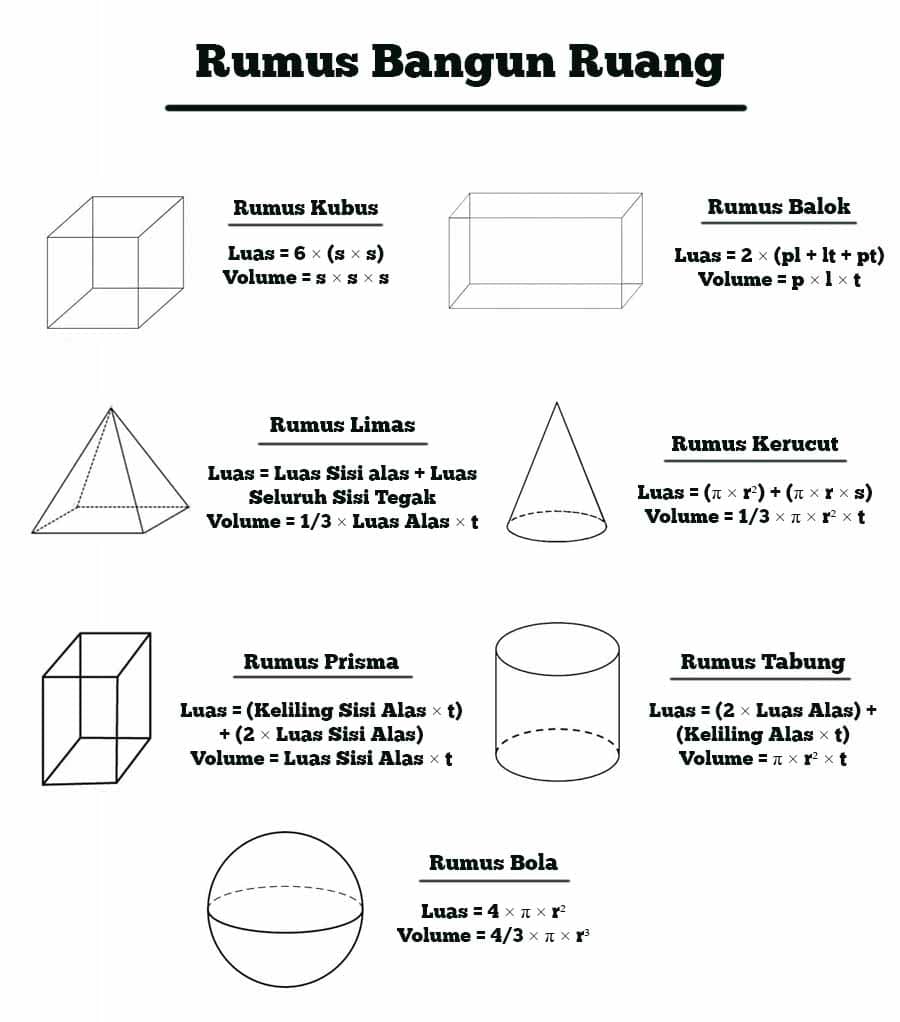
I. Rumus Luas Permukaan Bangun Ruang
Luas permukaan bangun ruang adalah jumlah luas keseluruhan permukaan pada bangun ruang tersebut. Rumus luas permukaan bangun ruang berbeda-beda tergantung pada jenis bangun ruang yang dimaksud. Berikut adalah rumus luas permukaan untuk beberapa jenis bangun ruang:
1. Kubus
Kubus adalah bangun ruang yang memiliki enam sisi yang sama besar dan sama bentuk. Setiap sisi kubus berbentuk persegi. Rumus luas permukaan kubus adalah sebagai berikut:
Lp = 6 x s x s
Keterangan:
Lp = luas permukaan
s = panjang sisi kubus
Contoh Soal:
Sebuah kubus memiliki panjang sisi 4 cm. Berapakah luas permukaan kubus tersebut?
Penyelesaian:
Lp = 6 x s x s
Lp = 6 x 4 x 4
Lp = 96 cm^2
Jadi, luas permukaan kubus tersebut adalah 96 cm^2.
2. Balok
Balok adalah bangun ruang yang memiliki lima sisi, yaitu dua sisi berbentuk persegi panjang dan tiga sisi berbentuk persegi. Rumus luas permukaan balok adalah sebagai berikut:
Lp = 2 x (p x l + p x t + l x t)
Keterangan:
Lp = luas permukaan
p = panjang balok
l = lebar balok
t = tinggi balok
Contoh Soal:
Sebuah balok memiliki panjang 10 cm, lebar 5 cm, dan tinggi 3 cm. Berapakah luas permukaan balok tersebut?
Penyelesaian:
Lp = 2 x (p x l + p x t + l x t)
Lp = 2 x (10 x 5 + 10 x 3 + 5 x 3)
Lp = 2 x (50 + 30 + 15)
Lp = 190 cm^2
Jadi, luas permukaan balok tersebut adalah 190 cm^2.
3. Prisma
Prisma adalah bangun ruang yang memiliki alas berbentuk segi-n dan sisi-sisi tegak berbentuk persegi atau persegi panjang. Rumus luas permukaan prisma adalah sebagai berikut:
Lp = (2 x luas alas) + (keliling alas x tinggi prisma)
Keterangan:
Lp = luas permukaan
luas alas = luas segi-n pada alas prisma
keliling alas = jumlah panjang sisi pada alas prisma
tinggi prisma = jarak antara alas dan tutup prisma
Contoh Soal:
Sebuah prisma segi-enam memiliki panjang sisi 5 cm dan tinggi prisma 7 cm. Berapakah luas permukaan prisma tersebut?
Penyelesaian:
Luas segi-n pada alas prisma = (3 x akar 3 x s^2)/2
Luas segi-n pada alas prisma = (3 x akar 3 x 5^2)/2
Luas segi-n pada alas prisma = 64,95 cm^2
Keliling alas = 6 x s
Keliling alas = 6 x 5
Keliling alas = 30 cm
Lp = (2 x luas alas) + (keliling alas x tinggi prisma)
Lp = (2 x 64,95) + (30 x 7)
Lp = 129,9 + 210
Lp = 339,9 cm^2
Jadi, luas permukaan prisma tersebut adalah 339,9 cm^2.
II. Rumus Volume Bangun Ruang
Volume bangun ruang adalah besaran yang menunjukkan ruang yang ditempati oleh suatu benda. Rumus volume bangun ruang juga berbeda-beda tergantung pada jenis bangun ruang yang dimaksud. Berikut adalah rumus volume untuk beberapa jenis bangun ruang:
1. Kubus
Rumus volume kubus adalah sebagai berikut:
V = s x s x s
Keterangan:
V = volume
s = panjang sisi kubus
Contoh Soal:
Sebuah kubus memiliki panjang sisi 5 cm. Berapakah volume kubus tersebut?
Penyelesaian:
V = s x s x s
V = 5 x 5 x 5
V = 125 cm^3
Jadi, volume kubus tersebut adalah 125 cm^3.
2. Balok
Rumus volume balok adalah sebagai berikut:
V = p x l x t
Keterangan:
V = volume
p = panjang balok
l = lebar balok
t = tinggi balok
Contoh Soal:
Sebuah balok memiliki panjang 8 cm, lebar 4 cm, dan tinggi 6 cm. Berapakah volume balok tersebut?
Penyelesaian:
V = p x l x t
V = 8 x 4 x 6
V = 192 cm^3
Jadi, volume balok tersebut adalah 192 cm^3.
3. Prisma
Rumus volume prisma adalah sebagai berikut:
V = luas alas x tinggi prisma
Keterangan:
V = volume
luas alas = luas segi-n pada alas prisma
tinggi prisma = jarak antara alas dan tutup prisma
Contoh Soal:
Sebuah prisma segi-enam memiliki panjang sisi 6 cm dan tinggi prisma 9 cm. Berapakah volume prisma tersebut?
Penyelesaian:
Luas segi-n pada alas prisma = (3 x akar 3 x s^2)/2
Luas segi-n pada alas prisma = (3 x akar 3 x 6^2)/2
Luas segi-n pada alas prisma = 93,53 cm^2
V = luas alas x tinggi prisma
V = 93,53 x 9
V = 841,77 cm^3
Jadi, volume prisma tersebut adalah 841,77 cm^3.
III. Kesimpulan
Setiap jenis bangun ruang memiliki rumus luas permukaan dan volume yang berbeda-beda. Untuk menghitung luas permukaan dan volume suatu benda, kita perlu mengetahui jenis bangun ruang yang dimaksud dan memahami rumusnya. Dalam artikel ini, telah dijelaskan rumus luas permukaan dan volume untuk kubus, balok, dan prisma, beserta contoh perhitungannya. Dengan memahami rumus-rumus tersebut, kita dapat lebih mudah dalam menghitung luas permukaan dan volume suatu benda.
 Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
