Belajar Rumus Vektor Satuan: Menghitung Besar Dan Arah Dengan Mudah

Rumus Vektor Satuan: Pengertian, Cara Menghitung, dan Contoh Soal

Vektor adalah salah satu konsep penting dalam matematika dan fisika. Vektor sering digunakan untuk menggambarkan arah dan besar suatu besaran, seperti kecepatan, percepatan, dan gaya. Namun, untuk menghitung besaran vektor dengan benar, kita perlu memahami rumus vektor satuan.

Pengertian Vektor Satuan

Vektor satuan adalah vektor yang memiliki magnitudo atau panjang satu. Dalam ilmu fisika dan matematika, vektor satuan sangat penting karena memungkinkan kita untuk menggambarkan arah dan besar suatu besaran secara akurat dan konsisten.

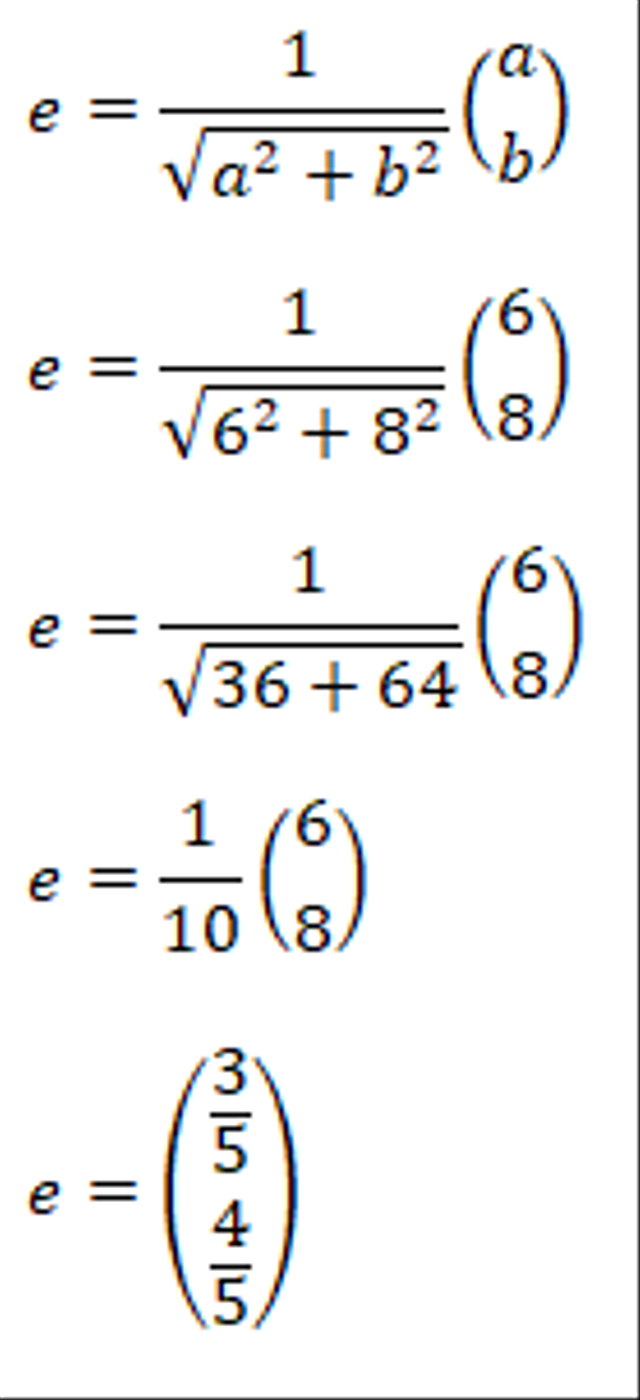
Untuk menghitung besaran vektor dengan benar, kita perlu membagi vektor dengan magnitudo atau besarnya. Dalam hal ini, vektor satuan dapat membantu kita membagi vektor dengan nilai yang tepat.

Cara Menghitung Vektor Satuan

Untuk menghitung vektor satuan, kita perlu mengikuti beberapa langkah sederhana. Berikut adalah cara menghitung vektor satuan:

Langkah 1: Cari Magnitudo Vektor

Langkah pertama dalam menghitung vektor satuan adalah menemukan magnitudo atau panjang vektor. Magnitudo vektor dapat dihitung dengan menggunakan rumus Pythagoras.

Contoh:
Diketahui vektor a = (3, 4). Hitunglah magnitudo vektor a.

Penyelesaian:
Magnitudo vektor a dapat dihitung dengan rumus Pythagoras:

|a| = sqrt(3^2 + 4^2)
|a| = sqrt(9 + 16)
|a| = sqrt(25)
|a| = 5

Jadi, magnitudo vektor a adalah 5.

Langkah 2: Bagi Vektor dengan Magnitudo

Setelah menemukan magnitudo vektor, langkah selanjutnya adalah membagi vektor dengan magnitudo tersebut. Hal ini dilakukan untuk menghasilkan vektor satuan.

Contoh:
Diketahui vektor b = (6, 8). Hitunglah vektor satuan dari vektor b.

Penyelesaian:
Vektor satuan dari vektor b dapat dihitung dengan membagi vektor b dengan magnitudo vektor b:

b^ = b / |b|
b^ = (6, 8) / 10
b^ = (0.6, 0.8)

Jadi, vektor satuan dari vektor b adalah (0.6, 0.8).

Contoh Soal Vektor Satuan

Berikut adalah beberapa contoh soal tentang vektor satuan beserta penyelesaiannya:

Contoh Soal 1

Diketahui vektor c = (2, 7). Hitunglah vektor satuan dari vektor c.

Penyelesaian:
Magnitudo vektor c dapat dihitung dengan rumus Pythagoras:

|c| = sqrt(2^2 + 7^2)
|c| = sqrt(4 + 49)
|c| = sqrt(53)

Vektor satuan dari vektor c dapat dihitung dengan membagi vektor c dengan magnitudo vektor c:

c^ = c / |c|
c^ = (2, 7) / sqrt(53)
c^ = (0.236, 0.972)

Jadi, vektor satuan dari vektor c adalah (0.236, 0.972).

Contoh Soal 2

Diketahui vektor d = (5, -12). Hitunglah vektor satuan dari vektor d.

Penyelesaian:
Magnitudo vektor d dapat dihitung dengan rumus Pythagoras:

|d| = sqrt(5^2 + (-12)^2)
|d| = sqrt(169)
|d| = 13

Vektor satuan dari vektor d dapat dihitung dengan membagi vektor d dengan magnitudo vektor d:

d^ = d / |d|
d^ = (5, -12) / 13
d^ = (0.385, -0.923)

Jadi, vektor satuan dari vektor d adalah (0.385, -0.923).

Contoh Soal 3

Diketahui vektor e = (3, 4). Hitunglah vektor satuan dari vektor e.

Penyelesaian:
Magnitudo vektor e dapat dihitung dengan rumus Pythagoras:

|e| = sqrt(3^2 + 4^2)
|e| = sqrt(25)
|e| = 5

Vektor satuan dari vektor e dapat dihitung dengan membagi vektor e dengan magnitudo vektor e:

e^ = e / |e|
e^ = (3, 4) / 5
e^ = (0.6, 0.8)

Jadi, vektor satuan dari vektor e adalah (0.6, 0.8).

Kesimpulan

Vektor satuan adalah salah satu konsep penting dalam matematika dan fisika. Vektor satuan digunakan untuk menghitung besaran vektor dengan benar dan akurat. Untuk menghitung vektor satuan, kita perlu menemukan magnitudo atau panjang vektor, lalu membagi vektor dengan magnitudo tersebut. Dengan rumus vektor satuan, kita dapat menggambarkan arah dan besar suatu besaran vektor dengan lebih akurat dan konsisten.