Rumus Matematika: Cara Mudah Mencari Luas Dan Keliling Segitiga Tumpul

Rumus Segitiga Tumpul: Pengenalan dan Konsep Dasar

Segitiga tumpul adalah segitiga yang memiliki salah satu sudutnya lebih besar dari 90 derajat. Dalam matematika, rumus segitiga tumpul adalah salah satu materi yang penting untuk dipelajari karena edukatif dan penting dalam konteks geometri.

Rumus segitiga tumpul terdiri dari beberapa elemen penting, di antaranya adalah panjang sisi-sisi segitiga, sudut-sudut yang terbentuk dalam segitiga tumpul, serta beberapa konsep matematika yang berkaitan dengan segitiga tumpul.

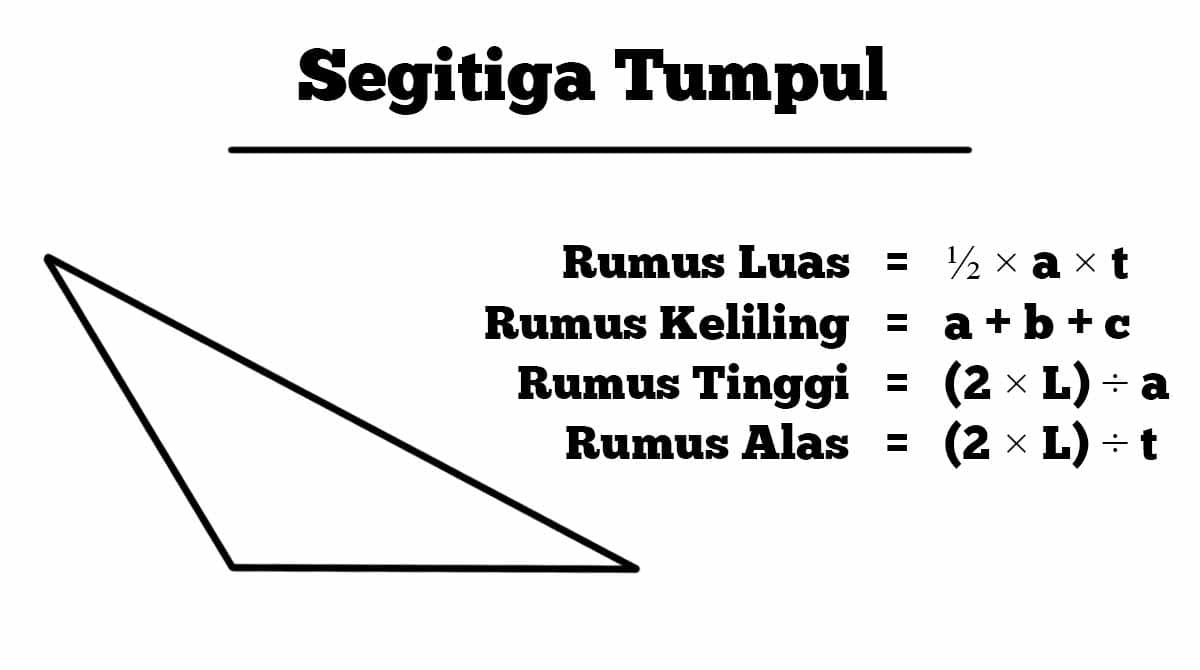
Berikut ini akan dijelaskan secara rinci mengenai rumus segitiga tumpul, termasuk definisi, sifat, dan cara menghitung panjang sisi-sisi segitiga tumpul.

Definisi dan Sifat Segitiga Tumpul

Segitiga tumpul adalah segitiga yang memiliki salah satu sudutnya lebih besar dari 90 derajat. Sudut tumpul ini disebut sebagai sudut segitiga tumpul. Sudut-sudut lainnya dalam segitiga tumpul memiliki ukuran yang lebih kecil dari 90 derajat.

Sebagaimana segitiga pada umumnya, segitiga tumpul juga memiliki tiga sisi dan tiga sudut. Namun, sisi yang bersebrangan dengan sudut segitiga tumpul, atau sisi terpanjang, disebut sebagai hipotenusa.

Sifat-sifat segitiga tumpul meliputi:

Segitiga tumpul hanya memiliki satu sudut tumpul.
Sudut-sudut lainnya pada segitiga tumpul selalu lebih kecil dari 90 derajat.
Sisi terpanjang pada segitiga tumpul selalu bersebrangan dengan sudut segitiga tumpul.
Segitiga tumpul dapat diletakkan di atas bidang datar atau dalam ruang tiga dimensi.

Perhitungan Panjang Sisi-sisi Segitiga Tumpul

Untuk menghitung panjang sisi-sisi segitiga tumpul, diperlukan beberapa rumus matematika, di antaranya adalah rumus Pythagoras dan rumus Trigonometri.

Rumus Pythagoras adalah rumus matematika yang digunakan untuk menghitung panjang sisi miring pada segitiga siku-siku. Rumus ini juga dapat digunakan dalam menghitung panjang sisi pada segitiga tumpul.

Rumus Pythagoras pada segitiga tumpul adalah sebagai berikut:
Diketahui: sisi a, sisi b, dan hipotenusa c
Ditanya: panjang sisi a atau sisi b

a = √(c² – b²)
b = √(c² – a²)

Contoh soal:
Diketahui sebuah segitiga tumpul dengan panjang sisi 8 cm dan 10 cm. Hitunglah panjang hipotenusa pada segitiga tumpul tersebut!

Penyelesaian:
Diketahui:
a = 8 cm
b = 10 cm

c = √(a² + b²)
c = √(8² + 10²)
c = √164
c = 12.81 cm

Jadi, panjang hipotenusa pada segitiga tumpul tersebut adalah 12.81 cm.

Selain menggunakan rumus Pythagoras, perhitungan panjang sisi pada segitiga tumpul juga dapat dilakukan dengan menggunakan rumus Trigonometri. Rumus ini lebih kompleks dibandingkan dengan rumus Pythagoras, namun lebih beragam dalam penggunaannya.

Rumus Trigonometri pada segitiga tumpul adalah sebagai berikut:
Diketahui: sisi a, sisi b, dan sudut C (sudut yang bersebrangan dengan hipotenusa c)
Ditanya: panjang sisi c atau sudut yang tidak diketahui

c = a / sin(C)
c = b / cos(C)
c = a / tan(C)
c = b / cot(C)

Contoh soal:
Diketahui sebuah segitiga tumpul dengan panjang sisi 8 cm, sudut C yang berhadapan dengan sisi 8 cm adalah 45 derajat, dan sudut A yang berhadapan dengan sisi 10 cm adalah 30 derajat. Hitunglah panjang sisi b pada segitiga tumpul tersebut!

Penyelesaian:
Diketahui:
a = 8 cm
sudut C = 45 derajat
sudut A = 30 derajat
sisi A = 10 cm

Mencari nilai sisi b dengan rumus Trigonometri:
b / sin(A) = c / sin(C)
b / sin(30) = c / sin(45)
b / 0.5 = c / 0.707
b = (0.5 x c) / 0.707

Mencari nilai sisi c dengan rumus Trigonometri:
c = a / sin(C)
c = 8 / 0.707
c = 11.31 cm

Substitusi nilai c pada rumus perhitungan sisi b:
b = (0.5 x c) / 0.707
b = (0.5 x 11.31) / 0.707
b = 8 cm

Jadi, panjang sisi b pada segitiga tumpul tersebut adalah 8 cm.

Konsep Matematika pada Segitiga Tumpul

Selain perhitungan panjang sisi pada segitiga tumpul, terdapat beberapa konsep matematika yang berkaitan dengan segitiga tumpul. Beberapa konsep tersebut antara lain:

1. Teorema Cosinus

Teorema Cosinus adalah teorema matematika yang berhubungan dengan perhitungan panjang sisi pada segitiga. Teorema ini dapat digunakan untuk menghitung panjang sisi pada segitiga tumpul.

Teorema Cosinus pada segitiga tumpul adalah sebagai berikut:
Diketahui: sisi a, sisi b, dan sudut C (sudut yang bersebrangan dengan hipotenusa c)
Ditanya: panjang sisi c atau sudut yang tidak diketahui

c² = a² + b² – 2ab cos(C)

Contoh soal:
Diketahui sebuah segitiga tumpul dengan panjang sisi 8 cm, sudut C yang berhadapan dengan sisi 8 cm adalah 45 derajat, dan sudut A yang berhadapan dengan sisi 10 cm adalah 30 derajat. Hitunglah panjang sisi c pada segitiga tumpul tersebut!

Penyelesaian:
Diketahui:
a = 8 cm
sudut C = 45 derajat
sudut A = 30 derajat
sisi A = 10 cm

Mencari nilai sisi c dengan rumus Teorema Cosinus:
c² = a² + b² – 2ab cos(C)
c² = 8² + 10² – 2(8 x 10 x cos(45))
c² = 214.28
c = 14.64 cm

Jadi, panjang sisi c pada segitiga tumpul tersebut adalah 14.64 cm.

2. Trigonometri pada Segitiga Tumpul

Trigonometri adalah cabang matematika yang berhubungan dengan perhitungan sudut dan segitiga. Dalam segitiga tumpul, Trigonometri dapat digunakan untuk menghitung sudut-sudut dalam segitiga tumpul.

Ada tiga jenis fungsi Trigonometri, yaitu sin, cos, dan tan. Ketiga fungsi ini digunakan dalam menghitung sudut-sudut dalam segitiga tumpul.

Contoh soal:
Diketahui sebuah segitiga tumpul dengan panjang sisi 8 cm, sudut C yang berhadapan dengan sisi 8 cm adalah 45 derajat, dan sudut A yang berhadapan dengan sisi 10 cm adalah 30 derajat. Hitunglah sudut B pada segitiga tumpul tersebut!

Penyelesaian:
Diketahui:
a = 8 cm
sudut C = 45 derajat
sudut A = 30 derajat
sisi A = 10 cm

Mencari nilai sudut B dengan rumus Trigonometri:
sin(B) = a / c
sin(B) = 8 / 14.64
sin(B) = 0.5463