Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Daftar Isi
Pengertian Rumus Segitiga Phytagoras
Rumus Segitiga Phytagoras adalah salah satu rumus matematika yang digunakan untuk menentukan panjang sisi miring segitiga siku-siku. Rumus ini ditemukan oleh seorang matematikawan Yunani kuno bernama Pythagoras. Rumus Segitiga Phytagoras juga dikenal dengan nama Teorema Pythagoras.
Rumus Segitiga Phytagoras
Rumus Segitiga Phytagoras dapat ditulis sebagai berikut:
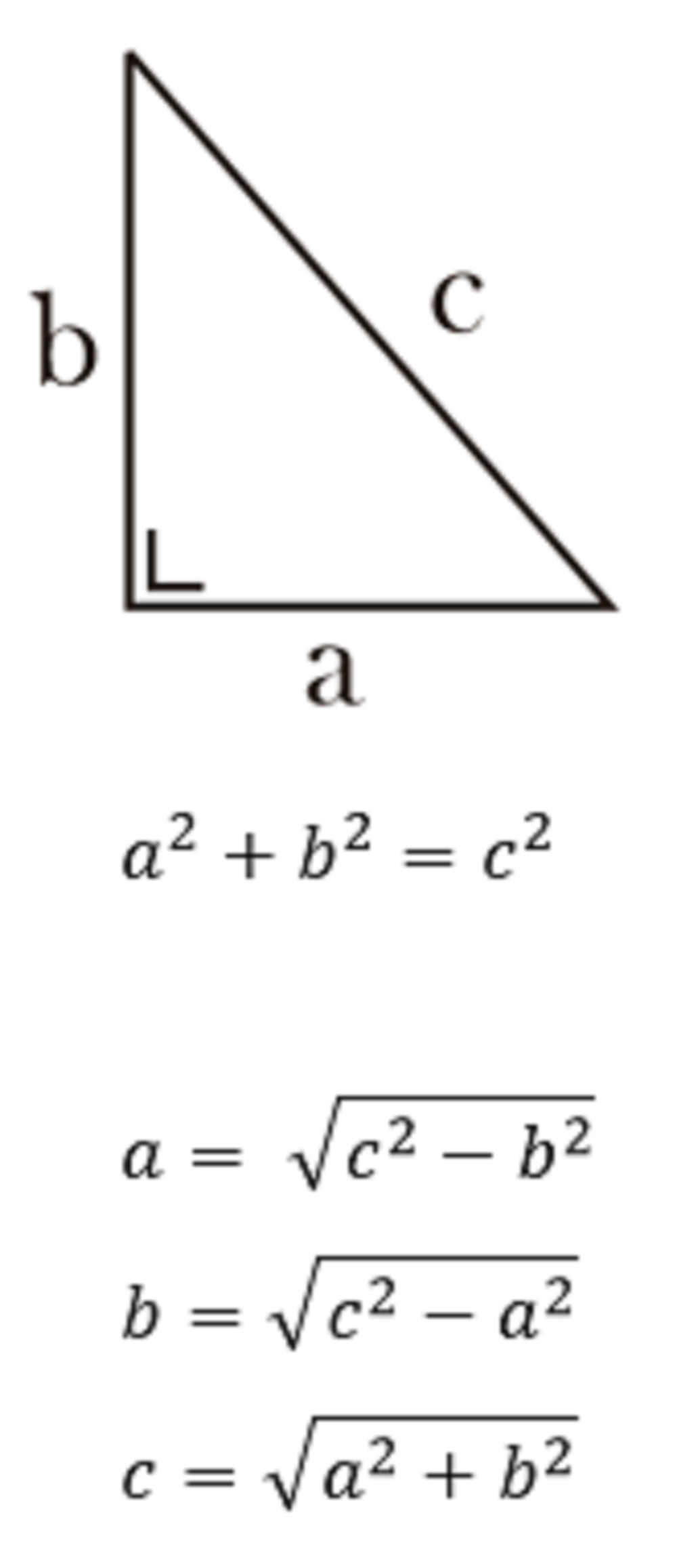
a² + b² = c²
dengan a dan b adalah panjang sisi-sisi yang membentuk sudut siku-siku, dan c adalah panjang sisi miring segitiga siku-siku.
Langkah-langkah Menggunakan Rumus Segitiga Phytagoras
Berikut adalah langkah-langkah dalam menggunakan Rumus Segitiga Phytagoras:
1. Tentukan sisi mana yang merupakan sisi miring segitiga siku-siku.
2. Identifikasi sisi-sisi mana yang merupakan sisi-sisi yang membentuk sudut siku-siku.
3. Berikan tanda a dan b pada sisi-sisi yang membentuk sudut siku-siku.
4. Gunakan rumus a² + b² = c² untuk mencari panjang sisi miring segitiga siku-siku.
5. Jika hanya diketahui panjang dua sisi yang membentuk sudut siku-siku, gunakan rumus invers dari Rumus Segitiga Phytagoras untuk mencari panjang sisi yang ketiga.
Contoh Soal Menggunakan Rumus Segitiga Phytagoras
Berikut adalah contoh soal yang dapat diselesaikan menggunakan Rumus Segitiga Phytagoras:
Contoh Soal 1:
Sebuah segitiga siku-siku memiliki panjang sisi-sisi yang membentuk sudut siku-siku sebesar 5 cm dan 12 cm. Tentukan panjang sisi miring segitiga tersebut.
Penyelesaian:
Langkah 1: Identifikasi sisi mana yang merupakan sisi miring segitiga siku-siku.
Dalam segitiga siku-siku, sisi yang membentuk sudut siku-siku selalu bersebrangan dengan sisi miring. Oleh karena itu, sisi miring dalam soal ini adalah sisi yang tidak diketahui.
Langkah 2: Identifikasi sisi-sisi mana yang merupakan sisi-sisi yang membentuk sudut siku-siku.
Dalam soal ini, sisi-sisi yang membentuk sudut siku-siku adalah 5 cm dan 12 cm.
Langkah 3: Berikan tanda a dan b pada sisi-sisi yang membentuk sudut siku-siku.
a = 5 cm
b = 12 cm
Langkah 4: Gunakan rumus a² + b² = c² untuk mencari panjang sisi miring segitiga siku-siku.
a² + b² = c²
5² + 12² = c²
25 + 144 = c²
169 = c²
c = akar(169)
c = 13 cm
Jadi, panjang sisi miring segitiga siku-siku dalam soal ini adalah 13 cm.
Contoh Soal 2:
Sebuah segitiga siku-siku memiliki panjang sisi-sisi yang membentuk sudut siku-siku sebesar 3 cm dan 4 cm. Tentukan panjang sisi yang ketiga.
Penyelesaian:
Langkah 1: Identifikasi sisi mana yang merupakan sisi miring segitiga siku-siku.
Dalam segitiga siku-siku, sisi yang membentuk sudut siku-siku selalu bersebrangan dengan sisi miring. Oleh karena itu, sisi miring dalam soal ini adalah sisi yang tidak diketahui.
Langkah 2: Identifikasi sisi-sisi mana yang merupakan sisi-sisi yang membentuk sudut siku-siku.
Dalam soal ini, sisi-sisi yang membentuk sudut siku-siku adalah 3 cm dan 4 cm.
Langkah 3: Berikan tanda a dan b pada sisi-sisi yang membentuk sudut siku-siku.
a = 3 cm
b = 4 cm
Langkah 4: Gunakan rumus invers dari Rumus Segitiga Phytagoras untuk mencari panjang sisi yang ketiga.
c² = a² + b²
c² = 3² + 4²
c² = 9 + 16
c² = 25
c = akar(25)
c = 5 cm
Jadi, panjang sisi yang ketiga dalam soal ini adalah 5 cm.
Kesimpulan
Rumus Segitiga Phytagoras sangat bermanfaat dalam menyelesaikan masalah matematika terutama dalam menentukan panjang sisi miring segitiga siku-siku. Oleh karena itu, penting bagi kita untuk memahami rumus ini dan bagaimana cara menggunakannya. Dengan memahami rumus ini, kita dapat menyelesaikan masalah matematika dengan lebih mudah dan cepat.
