Rumus Mudah Perhitungan Luas Dan Keliling Persegi: Mengenal Rumus Persegi Dengan Detail

Rumus-rumus Persegi: Pengenalan

Persegi adalah bangun datar yang memiliki empat sisi yang sama panjang dan memiliki empat sudut yang sama besarnya. Rumus-rumus persegi sangat penting untuk memahami sifat dan karakteristik dari bangun datar ini. Dalam artikel ini, akan dibahas tentang berbagai rumus-rumus persegi, langkah-langkah untuk menghitungnya, dan contoh-contoh penerapannya.

Rumus Keliling Persegi

Rumus keliling persegi adalah jumlah panjang keempat sisinya. Jika sisi persegi memiliki panjang s, maka rumus kelilingnya adalah:

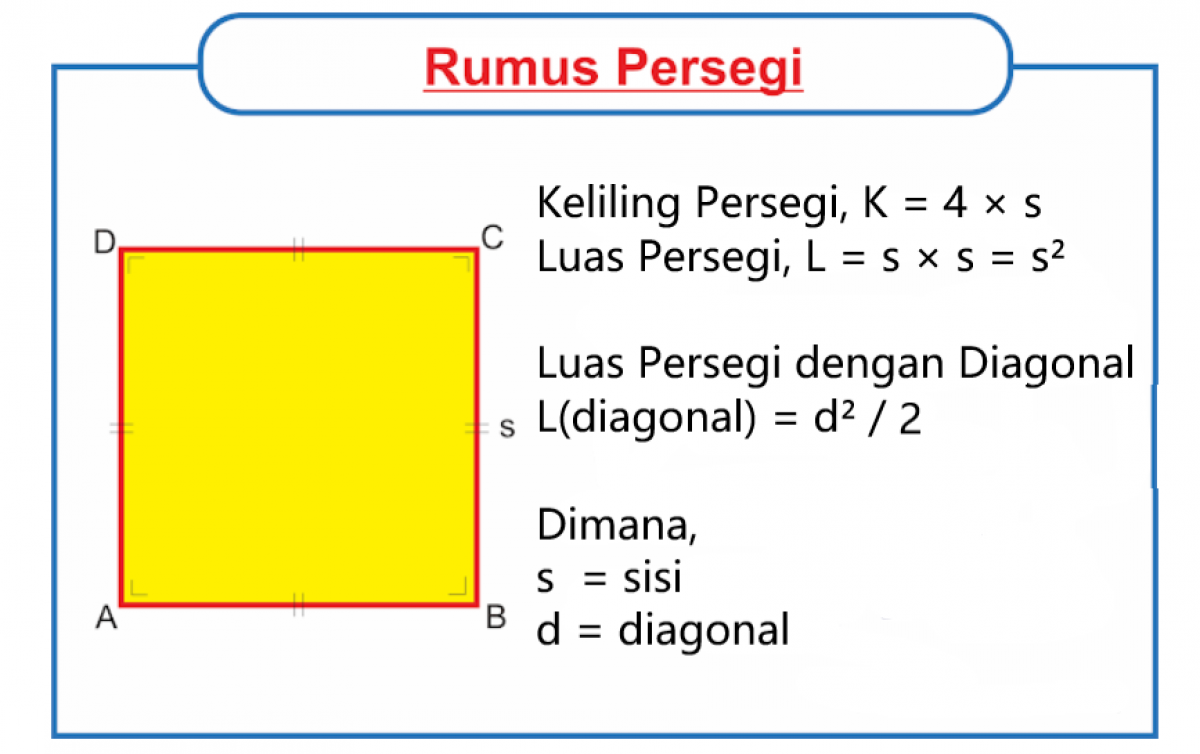
K = 4s

Keterangan:
– K: Keliling persegi
– s: Panjang sisi persegi

Contoh soal:

Sebuah persegi memiliki panjang sisi 12 cm. Hitunglah kelilingnya.

Penyelesaian:
K = 4s
K = 4 x 12
K = 48 cm

Jadi, keliling persegi adalah 48 cm.

Rumus Luas Persegi

Rumus luas persegi adalah panjang sisi persegi pangkat dua. Jika sisi persegi memiliki panjang s, maka rumus luasnya adalah:

L = s^2

Keterangan:
– L: Luas persegi
– s: Panjang sisi persegi

Contoh soal:

Sebuah persegi memiliki panjang sisi 8 cm. Hitunglah luasnya.

Penyelesaian:
L = s^2
L = 8^2
L = 64 cm^2

Jadi, luas persegi adalah 64 cm^2.

Rumus Diagonal Persegi

Rumus diagonal persegi adalah akar dari dua kali panjang sisi persegi. Jika sisi persegi memiliki panjang s, maka rumus diagonalnya adalah:

d = √2s

Keterangan:
– d: Panjang diagonal persegi
– s: Panjang sisi persegi

Contoh soal:

Sebuah persegi memiliki panjang sisi 6 cm. Hitunglah panjang diagonalnya.

Penyelesaian:
d = √2s
d = √2 x 6
d = √12 cm

Jadi, panjang diagonal persegi adalah √12 cm.

Rumus Keliling dan Luas Jajaran Genjang yang Bersebelahan Dua Sisi Merupakan Diagonal Persegi

Jajaran genjang adalah bangun datar yang memiliki dua pasang sisi sejajar dan sama panjang. Salah satu sifat jajaran genjang adalah bahwa dua diagonal yang menghubungkan ujung-ujung sisi-sisi yang tidak sejajar, merupakan diagonal persegi. Berikut adalah rumus keliling dan luas jajaran genjang yang bersebelahan dua sisinya merupakan diagonal persegi:

1. Rumus Keliling Jajaran Genjang

K = 2(a+b)

Keterangan:
– K: Keliling jajaran genjang
– a dan b: Panjang dua sisi yang bersebelahan dan merupakan diagonal persegi

Contoh soal:

Sebuah jajaran genjang memiliki dua sisi yang bersebelahan dan merupakan diagonal persegi, masing-masing memiliki panjang 8 cm dan 10 cm. Hitunglah keliling jajaran genjang.

Penyelesaian:
K = 2(a+b)
K = 2(8+10)
K = 36 cm

Jadi, keliling jajaran genjang adalah 36 cm.

2. Rumus Luas Jajaran Genjang

L = a x t

Keterangan:
– L: Luas jajaran genjang
– a: Panjang salah satu sisi yang merupakan diagonal persegi
– t: Tinggi jajaran genjang

Contoh soal:

Sebuah jajaran genjang memiliki dua sisi yang bersebelahan dan merupakan diagonal persegi, masing-masing memiliki panjang 8 cm dan 10 cm. Tinggi jajaran genjang adalah 6 cm. Hitunglah luas jajaran genjang.

Penyelesaian:
L = a x t
L = 8 x 6
L = 48 cm^2

Jadi, luas jajaran genjang adalah 48 cm^2.

Rumus Keliling dan Luas Belah Ketupat

Belah ketupat adalah bangun datar yang memiliki empat sisi yang sama panjang dan memiliki dua diagonal yang sama panjang serta saling membelah sudut menjadi dua sudut sama besar. Berikut adalah rumus keliling dan luas belah ketupat:

1. Rumus Keliling Belah Ketupat

K = 4s

Keterangan:
– K: Keliling belah ketupat
– s: Panjang sisi belah ketupat

Contoh soal:

Sebuah belah ketupat memiliki panjang sisi 7 cm. Hitunglah keliling belah ketupat.

Penyelesaian:
K = 4s
K = 4 x 7
K = 28 cm

Jadi, keliling belah ketupat adalah 28 cm.

2. Rumus Luas Belah Ketupat

L = ½ x d1 x d2

Keterangan:
– L: Luas belah ketupat
– d1 dan d2: Panjang kedua diagonal belah ketupat

Contoh soal:

Sebuah belah ketupat memiliki panjang diagonal 10 cm dan 12 cm. Hitunglah luas belah ketupat.

Penyelesaian:
L = ½ x d1 x d2
L = ½ x 10 x 12
L = 60 cm^2

Jadi, luas belah ketupat adalah 60 cm^2.

Kesimpulan

Dalam artikel ini, telah dijelaskan berbagai rumus-rumus persegi, seperti rumus keliling, luas, diagonal, keliling dan luas jajaran genjang yang bersebelahan dua sisinya merupakan diagonal persegi, serta rumus keliling dan luas belah ketupat. Semua rumus tersebut sangat penting untuk dipahami karena akan sering digunakan dalam menyelesaikan soal matematika, terutama yang berkaitan dengan persegi dan bangun datar lainnya. Dalam menghitung rumus-rumus tersebut, pastikan untuk memahami langkah-langkah dengan baik dan menggunakan rumus yang tepat agar hasilnya akurat.

Pencarian Berdasarkan Kata Kunci: persegi-