Rumus Pythagoras: Menghitung Sisi Miring Segitiga Dengan Tepat

Rumus Pythagoras Adalah

Rumus Pythagoras adalah salah satu rumus matematika yang paling terkenal di dunia. Rumus ini ditemukan oleh seorang ahli matematika Yunani bernama Pythagoras. Rumus ini digunakan untuk menghitung sisi miring segitiga siku-siku. Dalam bahasa Inggris, rumus Pythagoras disebut sebagai Pythagorean theorem.

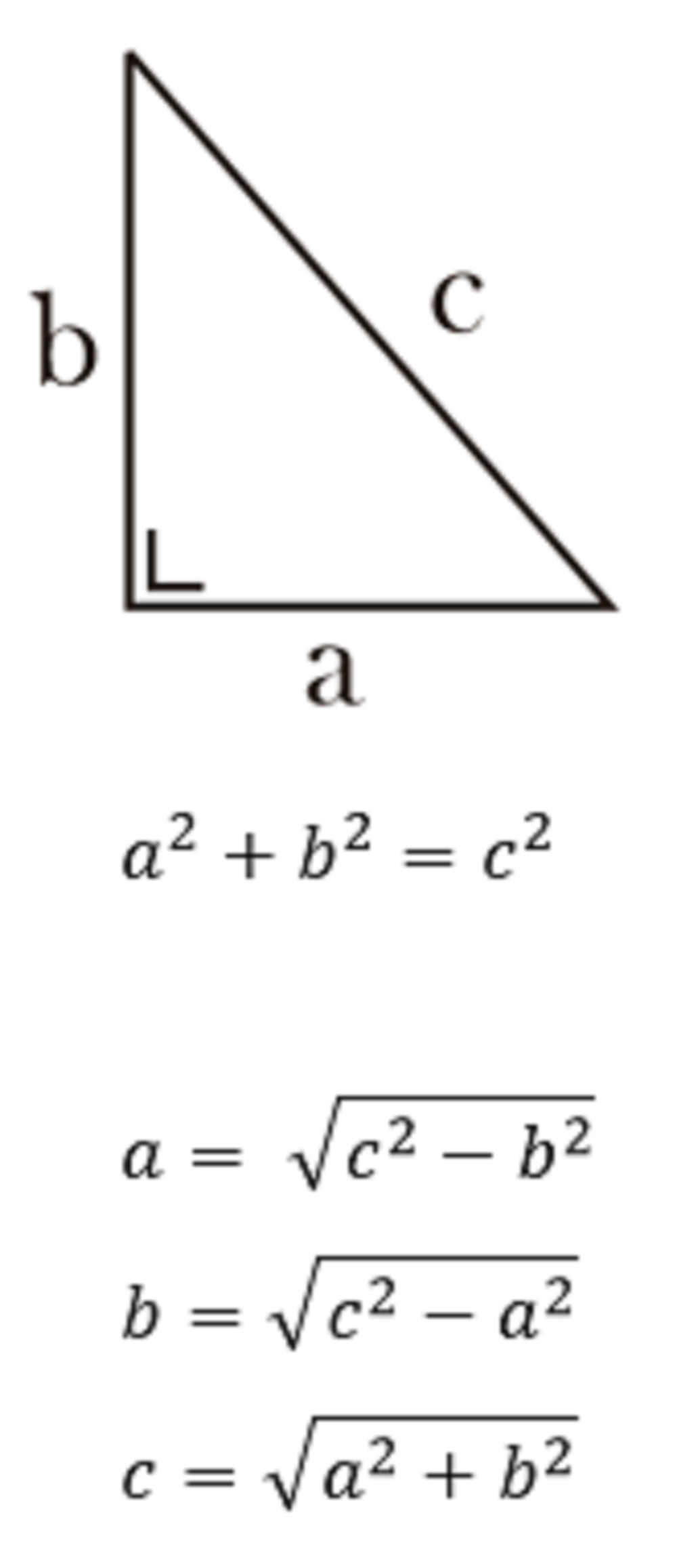
Pada dasarnya, rumus Pythagoras adalah cara menghitung panjang sisi miring sebuah segitiga siku-siku. Segitiga siku-siku adalah segitiga yang memiliki satu sudut siku-siku atau 90 derajat. Dalam segitiga siku-siku, sisi yang bersebrangan dengan sudut siku-siku disebut sebagai sisi miring atau hypotenuse. Sisi lainnya disebut sebagai kaki atau leg.

Rumus Pythagoras dapat dijelaskan dengan rumus matematika sebagai berikut:

c^2 = a^2 + b^2

Di mana c adalah panjang sisi miring, a dan b adalah panjang sisi kaki segitiga siku-siku. Oleh karena itu, untuk menghitung panjang sisi miring segitiga siku-siku, kita harus mengalikan kuadrat dari sisi kaki dan kemudian menambahkan hasilnya untuk mendapatkan kuadrat sisi miring. Setelah itu, kita dapat menghitung akar kuadrat dari hasil tersebut untuk mendapatkan panjang sisi miring.

Contoh:

Sebuah segitiga siku-siku memiliki sisi kaki sepanjang 3 cm dan 4 cm. Berapa panjang sisi miring segitiga tersebut?

Langkah 1: Identifikasi sisi kaki dan sisi miring

Dalam kasus ini, sisi kaki segitiga memiliki panjang 3 cm dan 4 cm. Sisi yang panjangnya tidak diketahui adalah sisi miring.

Langkah 2: Gunakan rumus Pythagoras

c^2 = a^2 + b^2

c^2 = 3^2 + 4^2

c^2 = 9 + 16

c^2 = 25

Langkah 3: Hitung akar kuadrat dari hasil

c = √25

c = 5 cm

Jadi, panjang sisi miring segitiga siku-siku adalah 5 cm.

Manfaat Rumus Pythagoras

Rumus Pythagoras memiliki banyak manfaat dalam kehidupan sehari-hari. Beberapa manfaatnya adalah sebagai berikut:

1. Arsitektur dan Desain

Rumus Pythagoras digunakan dalam arsitektur dan desain untuk menghitung panjang sisi miring pada bangunan dan struktur seperti atap, tangga, dan jembatan. Dengan menggunakan rumus Pythagoras, arsitek dan desainer dapat memastikan bahwa bangunan dan struktur yang mereka rancang aman dan stabil.

2. Matematika

Rumus Pythagoras adalah dasar dari banyak aspek matematika seperti trigonometri dan geometri. Dalam trigonometri, rumus Pythagoras digunakan untuk menghitung sisi miring segitiga non-siku-siku. Dalam geometri, rumus Pythagoras digunakan untuk menghitung jarak antara dua titik dalam ruang.

3. Fisika

Rumus Pythagoras juga digunakan dalam fisika untuk menghitung kecepatan dan percepatan benda. Dalam fisika, sisi miring segitiga siku-siku sering diartikan sebagai vektor atau besaran yang memiliki arah dan besar.

4. Elektronika

Rumus Pythagoras juga digunakan dalam elektronika untuk menghitung impedansi dan impedansi fase pada rangkaian listrik. Dalam elektronika, sisi miring segitiga siku-siku sering diartikan sebagai impedansi atau hambatan listrik.

Aturan Segitiga Siku-Siku

Selain rumus Pythagoras, ada juga aturan segitiga siku-siku yang digunakan untuk menyelesaikan masalah geometri yang melibatkan segitiga siku-siku. Aturan segitiga siku-siku adalah sebagai berikut:

1. Rasio sisi-sisi pada segitiga siku-siku

Dalam segitiga siku-siku, rasio sisi-sisi kaki dan sisi miring adalah 1 : √2 : 1.5. Artinya, jika kita mengalikan panjang sisi kaki dengan √2, maka kita akan mendapatkan panjang sisi miring.

Contoh:

Sebuah segitiga siku-siku memiliki sisi kaki sepanjang 6 cm. Berapa panjang sisi miring segitiga tersebut?

Langkah 1: Identifikasi sisi kaki dan sisi miring

Dalam kasus ini, sisi kaki segitiga memiliki panjang 6 cm. Sisi yang panjangnya tidak diketahui adalah sisi miring.

Langkah 2: Gunakan aturan segitiga siku-siku

Rasio sisi-sisi kaki dan sisi miring adalah 1 : √2 : 1.5. Oleh karena itu,

6 × √2 = 8.49

Langkah 3: Hitung hasil

Panjang sisi miring segitiga siku-siku adalah 8.49 cm.

2. Kombinasi sisi-sisi pada segitiga siku-siku

Dalam segitiga siku-siku, sisi kaki dan sisi miring dapat digabungkan untuk membentuk sisi lainnya. Misalnya, jika kita menggabungkan dua sisi kaki segitiga siku-siku, maka kita akan mendapatkan sisi miring.

Contoh:

Sebuah segitiga siku-siku memiliki sisi kaki sepanjang 3 cm dan 4 cm. Berapa panjang sisi lainnya pada segitiga tersebut?

Langkah 1: Identifikasi sisi kaki dan sisi miring

Dalam kasus ini, sisi kaki segitiga memiliki panjang 3 cm dan 4 cm. Sisi yang panjangnya tidak diketahui adalah sisi lainnya.

Langkah 2: Gunakan aturan segitiga siku-siku

Jika kita menggabungkan dua sisi kaki segitiga siku-siku, maka kita akan mendapatkan sisi miring. Oleh karena itu,

3 + 4 = 7

Langkah 3: Hitung hasil

Panjang sisi lainnya pada segitiga siku-siku adalah 7 cm.

Kesimpulan

Rumus Pythagoras adalah cara menghitung panjang sisi miring segitiga siku-siku. Rumus ini digunakan dalam banyak bidang seperti arsitektur, matematika, fisika, dan elektronika. Selain rumus Pythagoras, aturan segitiga siku-siku juga digunakan untuk menyelesaikan masalah geometri yang melibatkan segitiga siku-siku. Aturan segitiga siku-siku meliputi rasio sisi-sisi dan kombinasi sisi-sisi pada segitiga siku-siku.