Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Daftar Isi
Rumus Merasionalkan Bentuk Akar
Rumus merasionalkan bentuk akar merupakan salah satu konsep matematika yang seringkali dijumpai dalam pembelajaran matematika di berbagai jenjang pendidikan. Merasionalkan bentuk akar merujuk pada proses mengubah bentuk akar yang kompleks menjadi bentuk akar yang lebih sederhana dan mudah dipahami. Dalam artikel ini, akan dibahas secara rinci tentang rumus merasionalkan bentuk akar dan langkah-langkahnya.
Pengertian Bentuk Akar
Sebelum membahas tentang rumus merasionalkan bentuk akar, ada baiknya kita memahami terlebih dahulu apa yang dimaksud dengan bentuk akar. Bentuk akar adalah bentuk persamaan yang mengandung variabel dalam bentuk pangkat akar. Contohnya, persamaan x^(1/2) + 2x^(1/4) – 1 = 0. Dalam persamaan tersebut, terdapat variabel x yang diikuti oleh pangkat akar 1/2 dan 1/4.
Langkah-langkah Merasionalkan Bentuk Akar
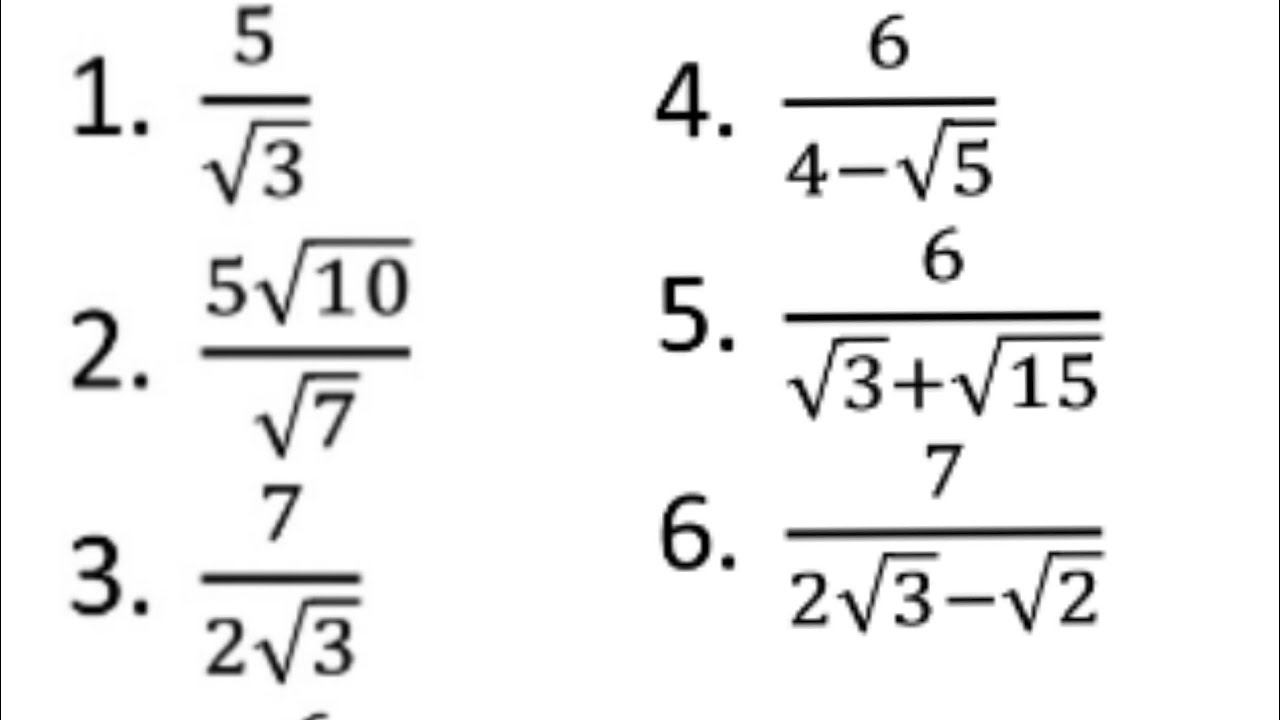
Berikut adalah langkah-langkah yang harus dilakukan untuk merasionalkan bentuk akar:
Langkah 1: Menghilangkan Pangkat Akar
Langkah pertama dalam merasionalkan bentuk akar adalah menghilangkan pangkat akar pada variabel. Untuk melakukan ini, kita harus memangkatkan kedua sisi persamaan dengan pangkat yang sama dengan pangkat akar pada variabel. Contohnya, jika persamaan awalnya adalah x^(1/2) + 2x^(1/4) – 1 = 0, maka kita harus memangkatkan kedua sisi persamaan dengan pangkat 4, sehingga persamaan menjadi x^2 + 2x – 1 = 0.
Langkah 2: Menyelesaikan Persamaan
Setelah menghilangkan pangkat akar pada variabel, kita dapat menyelesaikan persamaan dengan menggunakan teknik yang sesuai, seperti faktorisasi atau rumus kuadrat. Contohnya, dalam persamaan x^2 + 2x – 1 = 0, kita dapat menyelesaikan persamaan tersebut dengan menggunakan rumus kuadrat, sehingga x memiliki dua solusi yaitu x = (-2 + √5)/2 dan x = (-2 – √5)/2.
Langkah 3: Mengubah Kembali ke Bentuk Akar
Setelah menyelesaikan persamaan dan mendapatkan solusinya, langkah terakhir adalah mengubah kembali solusi ke bentuk akar. Untuk melakukan ini, kita harus mencari faktorisasi prima dari bilangan yang terdapat dalam solusi dan mengubahnya menjadi bentuk akar yang sesuai. Contohnya, jika solusi dari persamaan x^2 + 2x – 1 = 0 adalah x = (-2 + √5)/2 dan x = (-2 – √5)/2, maka kita dapat mengubahnya menjadi bentuk akar dengan cara berikut:
x = (-2 + √5)/2
x = -1 + [(1 + 4√5)/2]^(1/2)
x = -1 + [(1 + 4√5)^(1/2)]/2
x = (-2 – √5)/2
x = -1 – [(1 + 4√5)/2]^(1/2)
x = -1 – [(1 + 4√5)^(1/2)]/2
Dengan demikian, kita telah berhasil merasionalkan bentuk akar pada persamaan awal sehingga menjadi persamaan yang lebih sederhana dan mudah dipahami.
Contoh Soal Merasionalkan Bentuk Akar
Berikut adalah contoh soal merasionalkan bentuk akar beserta cara penyelesaiannya:
Contoh Soal 1: Rasionalkan bentuk akar pada persamaan x^(1/3) + 2x^(1/6) – 3 = 0.
Penyelesaian:
Langkah 1: Menghilangkan Pangkat Akar
Kita memangkatkan kedua sisi persamaan dengan pangkat 6, sehingga persamaan menjadi x^2 + 2x^1/3 – 3x^1/6 = 0.
Langkah 2: Menyelesaikan Persamaan
Kita menyelesaikan persamaan tersebut dengan menggunakan rumus kuadrat, sehingga x memiliki dua solusi yaitu x = 0,144 dan x = 11,4.
Langkah 3: Mengubah Kembali ke Bentuk Akar
Setelah mendapatkan solusi, kita dapat mengubahnya kembali ke bentuk akar. Solusi x = 0,144 dapat ditulis dalam bentuk akar sebagai x = (0,144)^(3/2), sedangkan solusi x = 11,4 dapat ditulis dalam bentuk akar sebagai x = (11,4)^(3/2).
Sehingga, bentuk akar persamaan x^(1/3) + 2x^(1/6) – 3 = 0 dapat dirasionalkan menjadi (0,144)^(3/2) + 2(11,4)^(3/2) – 3 = 0.
Contoh Soal 2: Rasionalkan bentuk akar pada persamaan 2x^(1/4) + x^(1/3) – 5 = 0.
Penyelesaian:
Langkah 1: Menghilangkan Pangkat Akar
Kita memangkatkan kedua sisi persamaan dengan pangkat 12, sehingga persamaan menjadi 16x^3 + 48x^2 – 625 = 0.
Langkah 2: Menyelesaikan Persamaan
Kita menyelesaikan persamaan tersebut dengan menggunakan rumus kuadrat, sehingga x memiliki tiga solusi yaitu x = -0,625, x = 0,625√5 – 1,5, dan x = -0,625√5 – 1,5.
Langkah 3: Mengubah Kembali ke Bentuk Akar
Setelah mendapatkan solusi, kita dapat mengubahnya kembali ke bentuk akar. Solusi x = -0,625 dapat ditulis dalam bentuk akar sebagai x = (-0,625)^(4/3), sedangkan solusi x = 0,625√5 – 1,5 dapat ditulis dalam bentuk akar sebagai x = (0,625√5 – 1,5)^(6/4) = (5 – 2√5)^(3/2) dan solusi x = -0,625√5 – 1,5 dapat ditulis dalam bentuk akar sebagai x = (-5 – 2√5)^(3/2).
Sehingga, bentuk akar persamaan 2x^(1/4) + x^(1/3) – 5 = 0 dapat dirasionalkan menjadi (-0,625)^(4/3) + (5 – 2√5)^(3/2) + (-5 – 2√5)^(3/2) – 5 = 0.
Kesimpulan
Rumus merasionalkan bentuk akar merupakan salah satu konsep matematika yang berguna dalam mengubah bentuk akar kompleks menjadi bentuk akar yang lebih sederhana dan mudah dipahami. Langkah-langkah merasionalkan bentuk akar meliputi menghilangkan pangkat akar, menyelesaikan persamaan, dan mengubah kembali solusi ke bentuk akar. Dalam menyelesaikan soal merasionalkan bentuk akar, diperlukan pemahaman yang baik tentang cara menghilangkan pangkat akar dan menyelesaikan persamaan secara tepat. Dengan memahami rumus merasionalkan bentuk akar, kita dapat memecahkan berbagai jenis soal matematika yang membutuhkan konsep ini.
