Daftar Isi
Rumus Menghitung Luas Segitiga
Segitiga adalah bangun datar yang memiliki tiga sisi dan tiga sudut. Segitiga memiliki banyak kegunaan di dalam matematika, fisika, dan berbagai bidang lainnya. Salah satu hal yang perlu dipahami dalam segitiga adalah cara menghitung luasnya. Luas segitiga merupakan ukuran bidang yang dihasilkan dari perkalian antara alas dan tinggi segitiga, dibagi dua. Berikut ini adalah rumus menghitung luas segitiga beserta penjelasan dan contohnya.
Pengertian Segitiga
Segitiga merupakan bangun datar yang memiliki tiga sisi dan tiga sudut. Sisi-sisi segitiga dapat dihitung menggunakan rumus jarak antara dua titik pada koordinat. Sementara itu, sudut-sudut segitiga dapat dihitung menggunakan rumus trigonometri. Ada beberapa jenis segitiga yang biasa dikenal, yaitu segitiga sama sisi, segitiga sama kaki, dan segitiga sembarang.
Rumus Menghitung Luas Segitiga
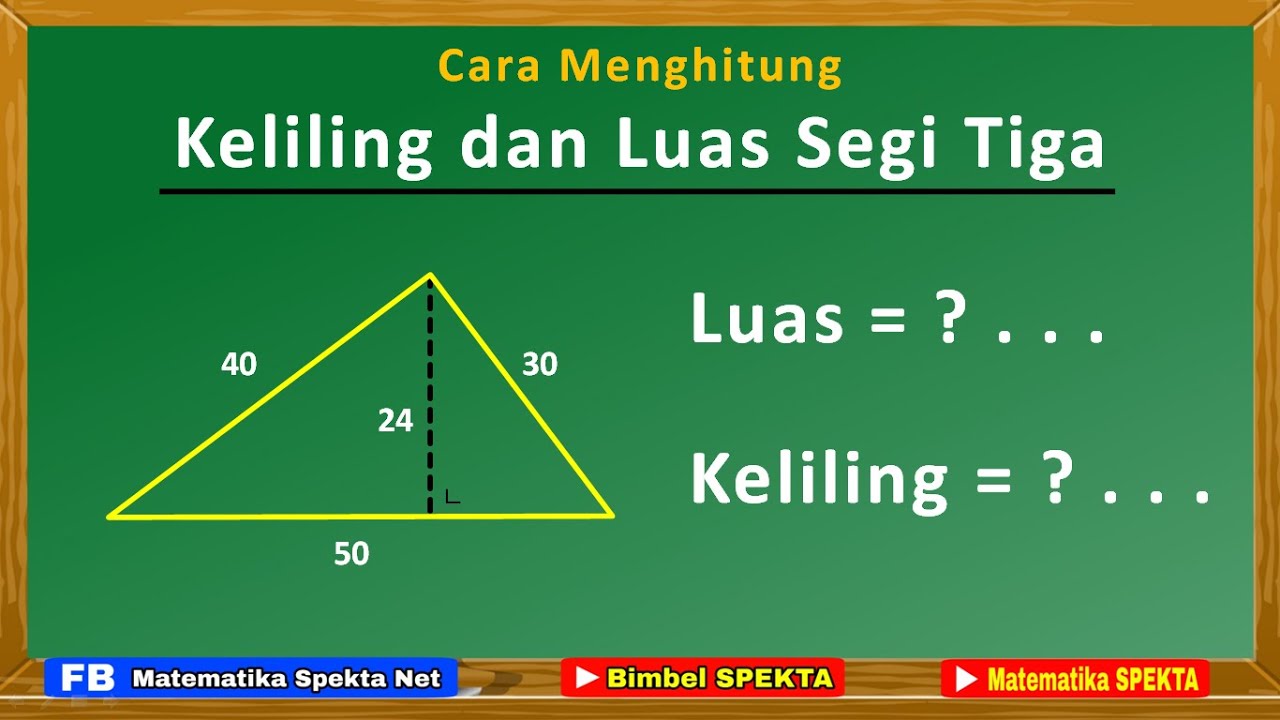
Luas segitiga dapat dihitung dengan menggunakan rumus dasar, yaitu:
Luas segitiga = 1/2 x alas x tinggi
Rumus tersebut mengambil setengah dari hasil perkalian antara alas dan tinggi segitiga. Selanjutnya, kita dapat menghitung alas dan tinggi segitiga terlebih dahulu sebelum mengaplikasikan rumus di atas.
Cara Menghitung Alas Segitiga
Alas segitiga merupakan sisi yang membatasi segitiga pada bagian bawah. Cara menghitung alas segitiga adalah:
1. Identifikasi sisi yang menjadi alas segitiga.
2. Ukur panjang sisi tersebut menggunakan penggaris atau alat ukur lainnya.
3. Catat hasil pengukuran dalam satuan yang digunakan (misalnya cm, m, atau km).
Contoh:
Diketahui segitiga ABC dengan panjang sisi AB sebesar 8 cm, sisi BC sebesar 6 cm, dan sisi AC sebesar 10 cm. Tentukan panjang alas segitiga.
Jawab:
Alas segitiga adalah sisi BC yang memiliki panjang 6 cm.
Cara Menghitung Tinggi Segitiga
Tinggi segitiga merupakan garis yang tegak lurus terhadap alas segitiga dan melewati titik puncak segitiga. Cara menghitung tinggi segitiga adalah:
1. Tentukan titik puncak segitiga.
2. Gambar garis yang tegak lurus terhadap alas segitiga dan melewati titik puncak tersebut.
3. Ukur panjang garis tersebut menggunakan penggaris atau alat ukur lainnya.
4. Catat hasil pengukuran dalam satuan yang digunakan (misalnya cm, m, atau km).
Contoh:
Diketahui segitiga ABC dengan panjang sisi AB sebesar 8 cm, sisi BC sebesar 6 cm, dan sisi AC sebesar 10 cm. Tentukan panjang tinggi segitiga.
Jawab:
Titik puncak segitiga adalah titik A. Garis yang tegak lurus terhadap BC dan melewati titik A adalah garis AD. Untuk menghitung panjang tinggi segitiga, kita perlu menghitung jarak dari titik A ke garis BC. Dalam hal ini, garis AD merupakan garis yang tegak lurus terhadap BC dan membagi BC menjadi dua bagian yang sama besar. Oleh karena itu, tinggi segitiga adalah 6 cm.
Contoh Soal
Diketahui segitiga ABC dengan panjang sisi AB sebesar 10 cm, sisi BC sebesar 8 cm, dan sisi AC sebesar 6 cm. Hitunglah luas segitiga tersebut.
Jawab:
1. Tentukan alas segitiga.
Alas segitiga adalah sisi BC yang memiliki panjang 8 cm.
2. Tentukan tinggi segitiga.
Untuk menghitung tinggi segitiga, kita perlu menghitung jarak dari titik A ke garis BC. Garis yang tegak lurus terhadap BC dan melewati titik A adalah garis AD. Oleh karena itu, tinggi segitiga adalah 3 cm.
3. Hitung luas segitiga menggunakan rumus:
Luas segitiga = 1/2 x alas x tinggi
= 1/2 x 8 cm x 3 cm
= 12 cm2
Jadi, luas segitiga ABC adalah 12 cm2.
Kesimpulan
Menghitung luas segitiga merupakan salah satu hal yang perlu dipahami dalam matematika. Luas segitiga dapat dihitung dengan menggunakan rumus dasar, yaitu 1/2 x alas x tinggi. Alas segitiga merupakan sisi yang membatasi segitiga pada bagian bawah, sedangkan tinggi segitiga merupakan garis yang tegak lurus terhadap alas segitiga dan melewati titik puncak segitiga. Untuk menghitung luas segitiga, kita perlu menghitung alas dan tinggi segitiga terlebih dahulu. Dalam hal ini, penggunaan rumus jarak antara dua titik pada koordinat sangat membantu untuk menghitung panjang sisi-sisi segitiga.
 Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
