Rumus Luas Permukaan
Rumus Luas Permukaan merujuk pada rumus matematika yang digunakan untuk menghitung luas permukaan sebuah objek tertentu. Dalam hal ini, luas permukaan mengacu pada area total permukaan objek tersebut. Rumus ini sangat penting dalam berbagai macam bidang, terutama dalam bidang matematika, fisika, dan teknik. Di bawah ini adalah beberapa rumus luas permukaan yang paling sering digunakan.
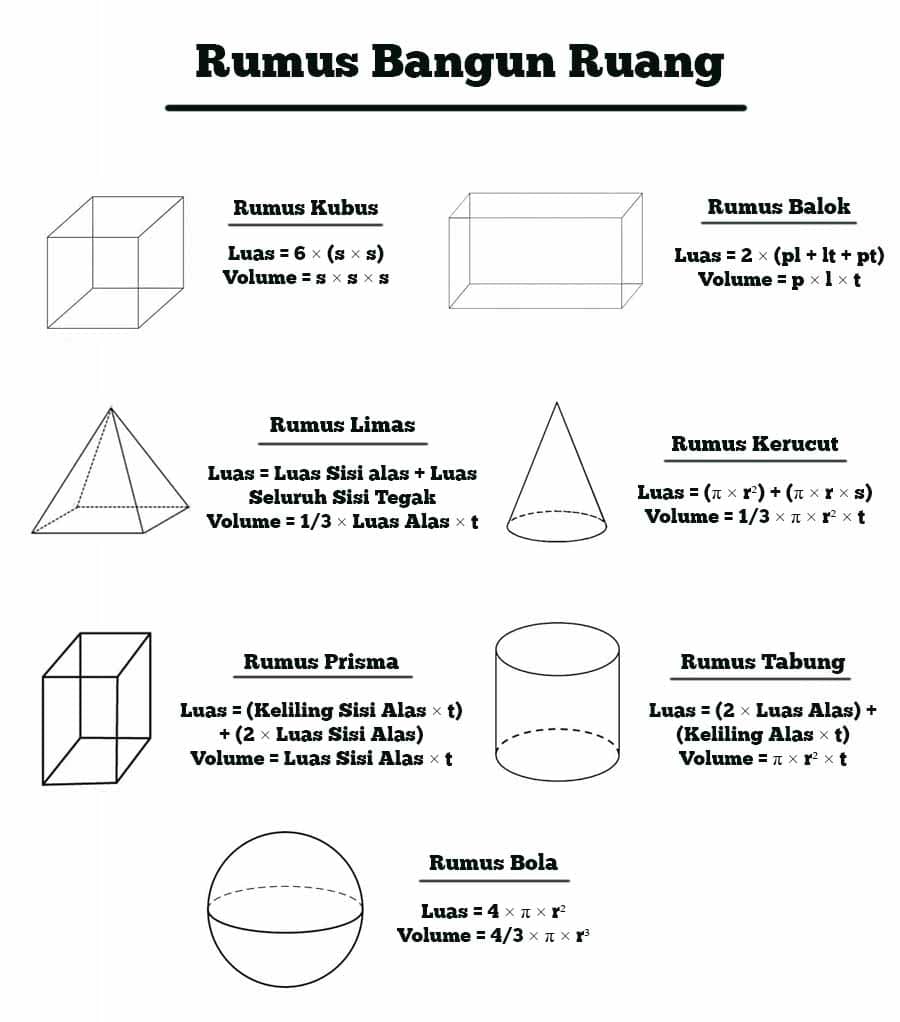
1. Rumus Luas Permukaan Kubus
Kubus adalah bentuk tiga dimensi yang memiliki enam sisi yang sama. Untuk menghitung luas permukaan kubus, kita perlu menghitung luas masing-masing sisi dan kemudian menjumlahkan hasilnya. Berikut adalah rumus untuk menghitung luas permukaan kubus:
Luas permukaan = 6 x sisi x sisi
Contoh Soal:
Sebuah kubus memiliki sisi yang panjangnya 5 cm, maka berapa luas permukaan kubus tersebut?
Penyelesaian:
Luas permukaan = 6 x sisi x sisi
Luas permukaan = 6 x 5 cm x 5 cm = 150 cm2
Jadi, luas permukaan kubus tersebut adalah 150 cm2.
2. Rumus Luas Permukaan Balok
Balok adalah bentuk tiga dimensi yang memiliki tiga pasang sisi yang sama. Untuk menghitung luas permukaan balok, kita perlu menghitung luas masing-masing sisi dan kemudian menjumlahkan hasilnya. Berikut adalah rumus untuk menghitung luas permukaan balok:
Luas permukaan = 2 x (panjang x lebar + panjang x tinggi + lebar x tinggi)
Contoh Soal:
Sebuah balok memiliki panjang 6 cm, lebar 4 cm, dan tinggi 3 cm, maka berapa luas permukaan balok tersebut?
Penyelesaian:
Luas permukaan = 2 x (panjang x lebar + panjang x tinggi + lebar x tinggi)
Luas permukaan = 2 x (6 cm x 4 cm + 6 cm x 3 cm + 4 cm x 3 cm) = 108 cm2
Jadi, luas permukaan balok tersebut adalah 108 cm2.
3. Rumus Luas Permukaan Tabung
Tabung adalah bentuk tiga dimensi yang terdiri dari sebuah lingkaran dan sebuah silinder. Untuk menghitung luas permukaan tabung, kita perlu menghitung luas lingkaran dan luas silinder kemudian menjumlahkan hasilnya. Berikut adalah rumus untuk menghitung luas permukaan tabung:
Luas permukaan = 2 x luas lingkaran + keliling lingkaran x tinggi
Luas Lingkaran = π x r2 (π = 22/7 atau 3,14)
Contoh Soal:
Sebuah tabung memiliki jari-jari 5 cm dan tinggi 12 cm, maka berapa luas permukaan tabung tersebut?
Penyelesaian:
Luas permukaan = 2 x luas lingkaran + keliling lingkaran x tinggi
Luas Lingkaran = π x r2
Luas Lingkaran = 22/7 x 5 cm x 5 cm = 78,57 cm2
Keliling lingkaran = 2 x π x r = 2 x 22/7 x 5 cm = 31,43 cm
Luas permukaan = 2 x 78,57 cm2 + 31,43 cm x 12 cm
Luas permukaan = 471,24 cm2
Jadi, luas permukaan tabung tersebut adalah 471,24 cm2.
4. Rumus Luas Permukaan Kerucut
Kerucut adalah bentuk tiga dimensi yang terdiri dari sebuah lingkaran dan sebuah kerucut. Untuk menghitung luas permukaan kerucut, kita perlu menghitung luas lingkaran dan luas kerucut kemudian menjumlahkan hasilnya. Berikut adalah rumus untuk menghitung luas permukaan kerucut:
Luas permukaan = luas selimut + luas lingkaran alas
Luas Selimut = π x r x s (s = √r2 + t2)
Luas Lingkaran = π x r2 (π = 22/7 atau 3,14)
Contoh Soal:
Sebuah kerucut memiliki jari-jari 7 cm dan tinggi 10 cm, maka berapa luas permukaan kerucut tersebut?
Penyelesaian:
Luas Selimut = π x r x s (s = √r2 + t2)
s = √72 + 102 = 12,21 cm
Luas Selimut = 22/7 x 7 cm x 12,21 cm = 269,43 cm2
Luas Lingkaran = π x r2
Luas Lingkaran = 22/7 x 7 cm x 7 cm = 153,86 cm2
Luas permukaan = luas selimut + luas lingkaran alas
Luas permukaan = 269,43 cm2 + 153,86 cm2 = 423,28 cm2
Jadi, luas permukaan kerucut tersebut adalah 423,28 cm2.
5. Rumus Luas Permukaan Bola
Bola adalah bentuk tiga dimensi yang terdiri dari semua titik yang berjarak sama dari titik pusat. Untuk menghitung luas permukaan bola, kita perlu menghitung luas permukaan bola yang dihasilkan oleh semua titik yang berjarak sama dari titik pusat. Berikut adalah rumus untuk menghitung luas permukaan bola:
Luas permukaan = 4 x π x r2 (π = 22/7 atau 3,14)
Contoh Soal:
Sebuah bola memiliki jari-jari 8 cm, maka berapa luas permukaan bola tersebut?
Penyelesaian:
Luas permukaan = 4 x π x r2
Luas permukaan = 4 x 22/7 x 8 cm x 8 cm = 804,24 cm2
Jadi, luas permukaan bola tersebut adalah 804,24 cm2.
Kesimpulan
Rumus Luas Permukaan sangat penting dalam berbagai macam bidang, terutama dalam bidang matematika, fisika, dan teknik. Dalam artikel ini, kami telah menjabarkan rumus luas permukaan untuk beberapa bentuk tiga dimensi yang paling sering digunakan, yaitu kubus, balok, tabung, kerucut, dan bola. Dengan memahami rumus ini, diharapkan dapat membantu Anda dalam menyelesaikan berbagai macam masalah yang berkaitan dengan luas permukaan objek tiga dimensi.
 Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
