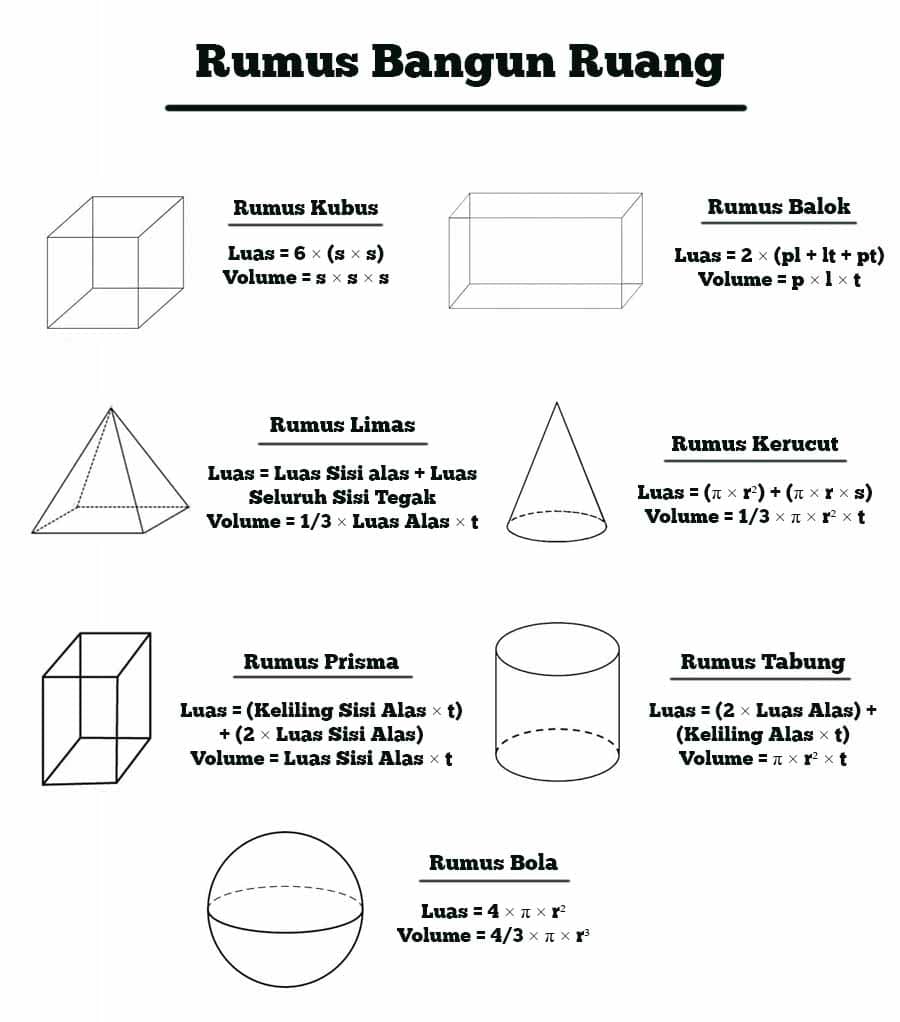
Rumus Bangun Ruang Sisi Lengkung
Bangun ruang sisi lengkung adalah salah satu jenis bangun ruang yang memiliki sisi lengkung atau melengkung. Bangun ruang ini memiliki beberapa jenis, seperti bola, kerucut, tabung, dan tembereng. Agar dapat menghitung volume atau luas permukaannya, diperlukan rumus bangun ruang sisi lengkung yang tepat. Berikut ini adalah penjelasan mengenai rumus bangun ruang sisi lengkung beserta contoh perhitungannya.
I. Rumus Bangun Ruang Sisi Lengkung Bola
Bola adalah bangun ruang sisi lengkung yang memiliki bentuk bulat sempurna dan memiliki jari-jari r. Untuk menghitung volume dan luas permukaan bola, digunakan rumus berikut ini:
1. Rumus Volume Bola
Rumus volume bola adalah 4/3πr^3, di mana:
– π (pi) = 22/7 atau 3,14
Contoh soal:
Sebuah bola memiliki jari-jari 7 cm. Hitunglah volume bola tersebut!
Penyelesaian:
Volume bola = 4/3 x π x r^3
= 4/3 x 22/7 x 7^3
= 1436,76 cm^3
Jadi, volume bola tersebut adalah 1436,76 cm^3.
2. Rumus Luas Permukaan Bola
Rumus luas permukaan bola adalah 4πr^2, di mana:
– π (pi) = 22/7 atau 3,14
Contoh soal:
Sebuah bola memiliki jari-jari 10 cm. Hitunglah luas permukaan bola tersebut!
Penyelesaian:
Luas permukaan bola = 4 x π x r^2
= 4 x 22/7 x 10^2
= 1256 cm^2
Jadi, luas permukaan bola tersebut adalah 1256 cm^2.
II. Rumus Bangun Ruang Sisi Lengkung Kerucut
Kerucut adalah bangun ruang sisi lengkung yang memiliki bentuk seperti kerucut pada tumpukan es krim. Kerucut memiliki jari-jari r, tinggi h, dan garis pelukis s. Untuk menghitung volume dan luas permukaan kerucut, digunakan rumus berikut ini:
1. Rumus Volume Kerucut
Rumus volume kerucut adalah 1/3πr^2h, di mana:
– π (pi) = 22/7 atau 3,14
Contoh soal:
Sebuah kerucut memiliki jari-jari 8 cm dan tinggi 12 cm. Hitunglah volume kerucut tersebut!
Penyelesaian:
Volume kerucut = 1/3 x π x r^2 x h
= 1/3 x 22/7 x 8^2 x 12
= 804,67 cm^3
Jadi, volume kerucut tersebut adalah 804,67 cm^3.
2. Rumus Luas Permukaan Kerucut
Rumus luas permukaan kerucut adalah πr^2 + πrs, di mana:
– π (pi) = 22/7 atau 3,14
– s = (r^2 + h^2)^0.5
Contoh soal:
Sebuah kerucut memiliki jari-jari 6 cm dan tinggi 10 cm. Hitunglah luas permukaan kerucut tersebut!
Penyelesaian:
Luas permukaan kerucut = πr^2 + πrs
= 22/7 x 6^2 + 22/7 x 6 x (6^2 + 10^2)^0.5
= 226,08 cm^2
Jadi, luas permukaan kerucut tersebut adalah 226,08 cm^2.
III. Rumus Bangun Ruang Sisi Lengkung Tabung
Tabung adalah bangun ruang sisi lengkung yang memiliki bentuk seperti kaleng minuman. Tabung memiliki jari-jari r, tinggi h, dan diameter d. Untuk menghitung volume dan luas permukaan tabung, digunakan rumus berikut ini:
1. Rumus Volume Tabung
Rumus volume tabung adalah πr^2h, di mana:
– π (pi) = 22/7 atau 3,14
Contoh soal:
Sebuah tabung memiliki jari-jari 4 cm dan tinggi 10 cm. Hitunglah volume tabung tersebut!
Penyelesaian:
Volume tabung = πr^2h
= 22/7 x 4^2 x 10
= 502,86 cm^3
Jadi, volume tabung tersebut adalah 502,86 cm^3.
2. Rumus Luas Permukaan Tabung
Rumus luas permukaan tabung adalah 2πr(h + r), di mana:
– π (pi) = 22/7 atau 3,14
Contoh soal:
Sebuah tabung memiliki jari-jari 5 cm dan tinggi 8 cm. Hitunglah luas permukaan tabung tersebut!
Penyelesaian:
Luas permukaan tabung = 2πr(h + r)
= 2 x 22/7 x 5 x (8 + 5)
= 314,28 cm^2
Jadi, luas permukaan tabung tersebut adalah 314,28 cm^2.
IV. Rumus Bangun Ruang Sisi Lengkung Tembereng
Tembereng adalah bangun ruang sisi lengkung yang memiliki bentuk seperti setengah bola. Tembereng memiliki jari-jari r dan tinggi h. Untuk menghitung volume dan luas permukaan tembereng, digunakan rumus berikut ini:
1. Rumus Volume Tembereng
Rumus volume tembereng adalah 1/6πh(3r^2 + h^2), di mana:
– π (pi) = 22/7 atau 3,14
Contoh soal:
Sebuah tembereng memiliki jari-jari 6 cm dan tinggi 4 cm. Hitunglah volume tembereng tersebut!
Penyelesaian:
Volume tembereng = 1/6πh(3r^2 + h^2)
= 1/6 x 22/7 x 4 x (3 x 6^2 + 4^2)
= 226,29 cm^3
Jadi, volume tembereng tersebut adalah 226,29 cm^3.
2. Rumus Luas Permukaan Tembereng
Rumus luas permukaan tembereng adalah πr^2 + rs, di mana:
– π (pi) = 22/7 atau 3,14
– s = (2rh – h^2)^0.5
Contoh soal:
Sebuah tembereng memiliki jari-jari 9 cm dan tinggi 6 cm. Hitunglah luas permukaan tembereng tersebut!
Penyelesaian:
Luas permukaan tembereng = πr^2 + rs
= 22/7 x 9^2 + 22/7 x 9 x [(2 x 9 x 6) – 6^2]^0.5
= 383,34 cm^2
Jadi, luas permukaan tembereng tersebut adalah 383,34 cm^2.
V. Kesimpulan
Dari penjelasan di atas, dapat disimpulkan bahwa untuk menghitung volume dan luas permukaan bangun ruang sisi lengkung, diperlukan rumus yang sesuai dengan jenis bangun ruang tersebut. Rumus tersebut meliputi rumus volume dan rumus luas permukaan. Jenis bangun ruang sisi lengkung yang umum digunakan adalah bola, kerucut, tabung, dan tembereng. Dengan mengetahui rumus bangun ruang sisi lengkung, maka dapat dengan mudah menghitung volume dan luas permukaan bangun ruang tersebut.
 Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
