Rumus Bangun Ruang Lengkap Untuk Menghitung Volume Dan Luas Permukaan Dengan Mudah

Rumus Bangun Ruang Lengkap

Bangun ruang adalah benda geometris tiga dimensi yang memiliki luas permukaan dan volume tertentu. Ada beberapa macam bangun ruang, seperti kubus, balok, bola, kerucut, dan prisma. Setiap bangun ruang memiliki rumus yang berbeda-beda untuk menghitung luas permukaan dan volume. Pada artikel ini, akan dijelaskan rumus bangun ruang lengkap beserta contoh soalnya.

Kubus

Kubus adalah bangun ruang yang memiliki enam sisi yang sama besar dan bentuknya sama-sama persegi. Rumus kubus adalah sebagai berikut:

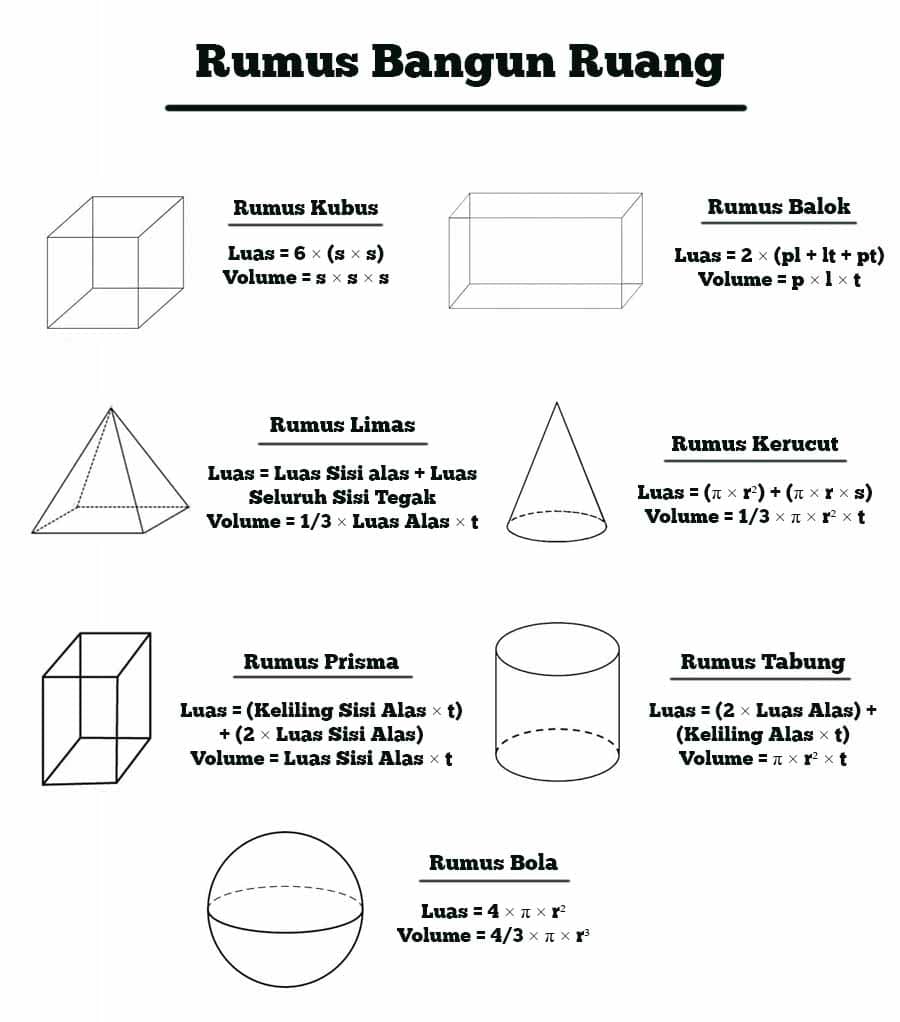
– Luas permukaan kubus: 6 x sisi x sisi
– Volume kubus: sisi x sisi x sisi

Contoh soal:

Sebuah kubus memiliki sisi sepanjang 5 cm. Hitunglah luas permukaan dan volume kubus tersebut.

Penyelesaian:

– Luas permukaan kubus: 6 x 5 x 5 = 150 cm2
– Volume kubus: 5 x 5 x 5 = 125 cm3

Jadi, luas permukaan kubus tersebut adalah 150 cm2 dan volume kubusnya adalah 125 cm3.

Balok

Balok adalah bangun ruang yang memiliki tiga pasang sisi yang sama besar dan saling bersebrangan, serta memiliki bentuk persegi panjang. Rumus balok adalah sebagai berikut:

– Luas permukaan balok: 2 x (panjang x lebar + panjang x tinggi + lebar x tinggi)
– Volume balok: panjang x lebar x tinggi

Contoh soal:

Sebuah balok memiliki panjang 10 cm, lebar 5 cm, dan tinggi 6 cm. Hitunglah luas permukaan dan volume balok tersebut.

Penyelesaian:

– Luas permukaan balok: 2 x (10 x 5 + 10 x 6 + 5 x 6) = 220 cm2
– Volume balok: 10 x 5 x 6 = 300 cm3

Jadi, luas permukaan balok tersebut adalah 220 cm2 dan volume baloknya adalah 300 cm3.

Bola

Bola adalah bangun ruang yang memiliki bentuk bulat sempurna. Rumus bola adalah sebagai berikut:

– Luas permukaan bola: 4 x π x r2
– Volume bola: 4/3 x π x r3

Keterangan: π (pi) = 22/7 atau 3,14, dan r adalah jari-jari bola.

Contoh soal:

Sebuah bola memiliki jari-jari sepanjang 8 cm. Hitunglah luas permukaan dan volume bola tersebut.

Penyelesaian:

– Luas permukaan bola: 4 x 22/7 x 82 = 804,57 cm2
– Volume bola: 4/3 x 22/7 x 83 = 2143,67 cm3

Jadi, luas permukaan bola tersebut adalah 804,57 cm2 dan volume bolanya adalah 2143,67 cm3.

Kerucut

Kerucut adalah bangun ruang yang memiliki bentuk seperti kerucut. Rumus kerucut adalah sebagai berikut:

– Luas permukaan kerucut: π x r x (r + s)
– Volume kerucut: 1/3 x π x r2 x t

Keterangan: s adalah garis pelukis kerucut dan t adalah tinggi kerucut.

Contoh soal:

Sebuah kerucut memiliki jari-jari sepanjang 6 cm dan tinggi 8 cm. Hitunglah luas permukaan dan volume kerucut tersebut.

Penyelesaian:

– Luas permukaan kerucut: 22/7 x 6 x (6 + √(82 + 62)) = 201,06 cm2
– Volume kerucut: 1/3 x 22/7 x 62 x 8 = 100,48 cm3

Jadi, luas permukaan kerucut tersebut adalah 201,06 cm2 dan volume kerucutnya adalah 100,48 cm3.

Prisma

Prisma adalah bangun ruang yang memiliki dua sisi yang sama besar dan sejajar. Rumus prisma adalah sebagai berikut:

– Luas permukaan prisma: luas alas + (keliling alas x tinggi) + (jumlah luas sisi tegak x tinggi)
– Volume prisma: luas alas x tinggi

Contoh soal:

Sebuah prisma segitiga memiliki alas sepanjang 6 cm, tinggi segitiga 8 cm, dan tinggi prisma 10 cm. Hitunglah luas permukaan dan volume prisma tersebut.

Penyelesaian:

– Luas permukaan prisma: 1/2 x 6 x 8 + (3 x 6 x 10) + (3 x 8 x 10) = 276 cm2
– Volume prisma: 1/2 x 6 x 8 x 10 = 240 cm3

Jadi, luas permukaan prisma segitiga tersebut adalah 276 cm2 dan volume prismanya adalah 240 cm3.

Kesimpulan

Setiap bangun ruang memiliki rumus yang berbeda-beda untuk menghitung luas permukaan dan volume. Rumus-rumus tersebut dapat dihitung dengan mudah jika kita memahami konsep dan kaidah dasar matematika. Dengan menguasai rumus-rumus bangun ruang, kita bisa menyelesaikan berbagai macam soal matematika yang berhubungan dengan bangun ruang.