Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Daftar Isi
Pengantar
Pythagoras Segitiga adalah salah satu teorema matematika yang paling terkenal dan fundamental. Teorema ini menghubungkan sisi-sisi segitiga siku-siku dengan panjang sisi-sisi tersebut. Teorema Pythagoras ditemukan oleh matematikawan Yunani kuno bernama Pythagoras, dan hingga kini, teorema ini masih sering digunakan dalam berbagai bidang. Dalam artikel ini, kita akan membahas Pythagoras Segitiga secara detail.
Definisi
Pythagoras Segitiga adalah segitiga yang salah satu sudutnya merupakan sudut siku-siku. Teorema Pythagoras menyatakan bahwa kuadrat panjang sisi miring (hipotenusa) sama dengan jumlah kuadrat panjang kedua sisi lainnya.
Sejarah
Teorema Pythagoras dinamakan berdasarkan nama matematikawan Yunani kuno, Pythagoras. Salah satu legenda menyatakan bahwa Pythagoras menemukan teorema ini ketika ia memperhatikan suara yang dihasilkan ketika memukul tali instrumen musik yang berbeda panjangnya. Dia kemudian menyadari bahwa panjang tali instrumen musik tersebut berhubungan dengan suara yang dihasilkan dan mengembangkan teorema yang sekarang kita kenal sebagai Pythagoras Segitiga.
Namun, terdapat beberapa klaim bahwa teorema ini sudah dikenal sebelum Pythagoras. Sebagai contohnya, kebudayaan Mesir dan Babilonia sudah menggunakan teorema yang mirip dengan Pythagoras Segitiga sekitar 1000 tahun sebelum Pythagoras lahir.
Teorema Pythagoras
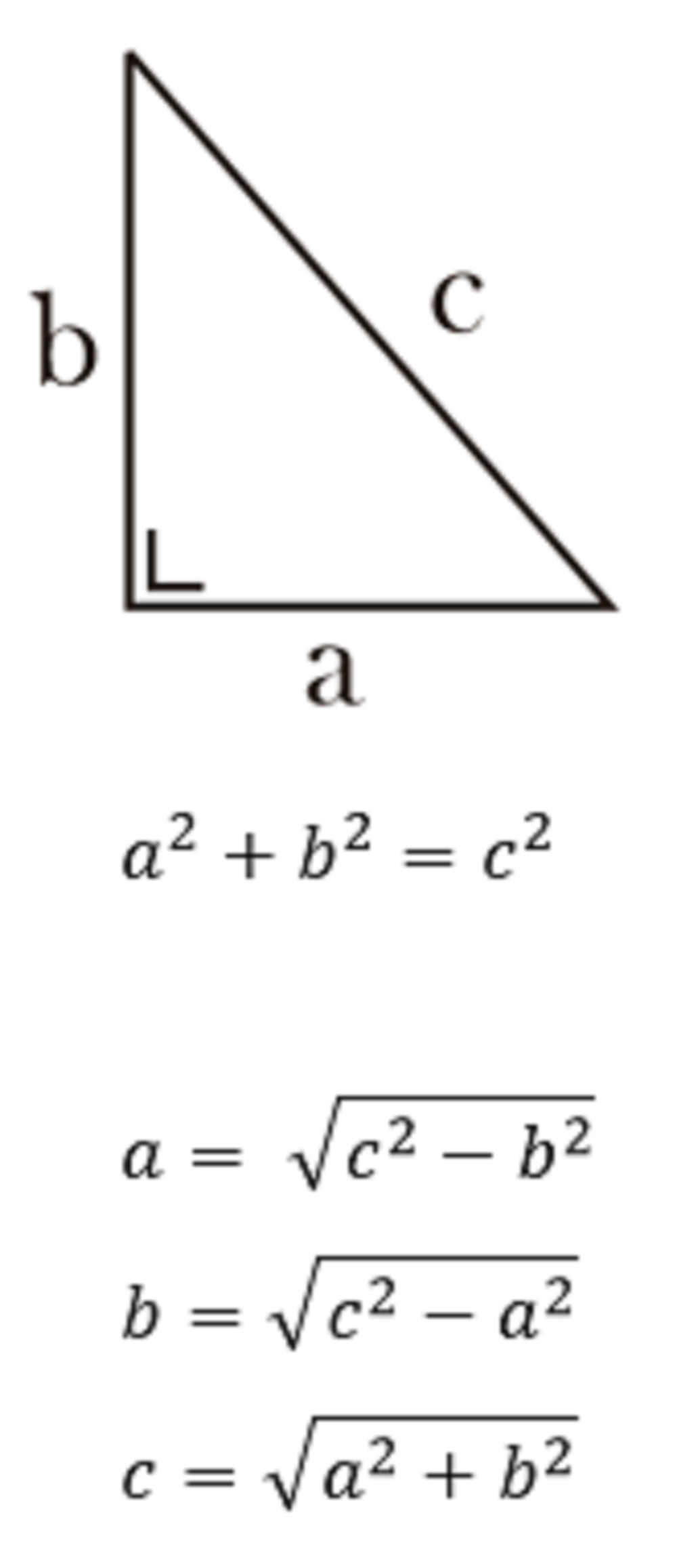
Teorema Pythagoras menyatakan bahwa dalam sebuah segitiga siku-siku, kuadrat panjang sisi miring sama dengan jumlah kuadrat panjang kedua sisi lainnya. Dalam bentuk matematika, teorema Pythagoras dapat dituliskan sebagai berikut:
a^2 + b^2 = c^2
Di mana a dan b mewakili panjang sisi-sisi yang bertemu di sudut siku-siku, dan c mewakili panjang sisi miring.
Contoh Soal
Contoh Soal 1:
Sebuah segitiga memiliki sisi-sisi 6 cm, 8 cm, dan 10 cm. Apakah segitiga tersebut merupakan segitiga siku-siku?
Jawab:
Kita dapat menggunakan teorema Pythagoras untuk memeriksa apakah segitiga tersebut merupakan segitiga siku-siku atau tidak.
a^2 + b^2 = c^2
6^2 + 8^2 = 10^2
36 + 64 = 100
100 = 100
Karena sisi-sisi segitiga tersebut memenuhi persamaan tersebut, maka segitiga tersebut merupakan segitiga siku-siku.
Contoh Soal 2:
Jika sebuah segitiga siku-siku memiliki sisi-sisi 5 cm dan 12 cm, berapa panjang sisi miringnya?
Jawab:
Kita dapat menggunakan teorema Pythagoras untuk mencari panjang sisi miring.
a^2 + b^2 = c^2
5^2 + 12^2 = c^2
25 + 144 = c^2
169 = c^2
c = √169
c = 13
Jadi, panjang sisi miring segitiga tersebut adalah 13 cm.
Aplikasi
Teorema Pythagoras banyak digunakan dalam berbagai bidang, termasuk dalam matematika, fisika, dan teknik. Beberapa aplikasi dari teorema Pythagoras antara lain:
1. Menghitung jarak antara dua titik
Teorema Pythagoras digunakan untuk menghitung jarak antara dua titik dalam koordinat kartesius.
2. Membuat bangun datar
Teorema Pythagoras digunakan untuk membuat bangun datar, seperti segitiga siku-siku, persegi, persegi panjang, dan lain-lain.
3. Membuat bangun ruang
Teorema Pythagoras digunakan untuk membuat bangun ruang, seperti kubus dan prisma.
4. Membuat rumus trigonometri
Rumus trigonometri seperti sin, cos, dan tan juga didasarkan pada teorema Pythagoras.
Kesimpulan
Pythagoras Segitiga adalah salah satu teorema matematika paling terkenal dan fundamental. Teorema ini menghubungkan sisi-sisi segitiga siku-siku dengan panjang sisi-sisi tersebut. Teorema Pythagoras ditemukan oleh matematikawan Yunani kuno bernama Pythagoras, dan hingga kini, teorema ini masih sering digunakan dalam berbagai bidang. Teorema Pythagoras sangat penting karena dapat digunakan untuk mencari panjang sisi miring dalam segitiga siku-siku dan digunakan dalam berbagai aplikasi matematika, fisika, dan teknik.
