Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Daftar Isi
Mencari Sudut Segitiga
Sudut segitiga merupakan salah satu konsep dasar dalam geometri. Sudut segitiga memiliki peran penting dalam berbagai bidang, seperti matematika, fisika, teknik, dan lain sebagainya. Sudut segitiga adalah sudut yang terbentuk oleh dua sisi segitiga. Pada artikel ini, kita akan membahas tentang cara mencari sudut segitiga dengan mudah.
Poin Penting:
1. Sudut merupakan perpotongan antara dua garis atau lebih.
2. Sudut segitiga terbentuk oleh dua sisi segitiga.
3. Sudut segitiga dapat dibagi menjadi tiga jenis, yaitu sudut lancip, sudut tumpul, dan sudut siku-siku.
Langkah-langkah untuk Mencari Sudut Segitiga:
1. Mencari Sudut dengan Menggunakan Trigonometri:
– Trigonometri adalah cabang ilmu matematika yang berhubungan dengan perbandingan antara sisi-sisi segitiga dengan sudut yang membentuk segitiga tersebut.
– Untuk mencari sudut segitiga dengan menggunakan trigonometri, kita perlu mengetahui nilai dari dua sisi segitiga dan satu sudut yang membentuk segitiga tersebut.
– Dalam trigonometri, terdapat tiga fungsi trigonometri yang dapat digunakan, yaitu sin, cos, dan tan.
– Rumus untuk mencari sudut segitiga adalah sebagai berikut:
sin A = (sisi yang bersebrangan dengan sudut A) / (panjang sisi miring)
cos A = (sisi yang bersebrangan dengan sudut A) / (panjang sisi alas)
tan A = (sisi yang bersebrangan dengan sudut A) / (sisi sejajar)
– Setelah mengetahui nilai dari salah satu fungsi trigonometri, kita dapat mencari nilai sudut dengan menggunakan alat kalkulator atau tabel trigonometri.
Contoh Soal:
Diketahui sebuah segitiga ABC dengan panjang sisi AB = 6 cm, sisi AC = 8 cm, dan sudut BAC = 60 derajat. Tentukanlah ukuran sudut ABC dan sudut ACB.
Penyelesaian:
Pertama-tama, kita dapat menggunakan fungsi sin untuk mencari nilai sudut ABC.
Sin (ABC) = (sisi yang bersebrangan dengan sudut ABC) / (panjang sisi miring)
Sin (ABC) = (6) / (8)
Sin (ABC) = 0,75
Kita dapat mencari nilai sudut ABC dengan menggunakan tabel trigonometri atau alat kalkulator.
Sin-1 (0,75) = 48,59 derajat
Jadi, sudut ABC memiliki ukuran sebesar 48,59 derajat.
Untuk mencari sudut ACB, kita dapat menggunakan rumus:
Sudut ACB = 180 – sudut BAC – sudut ABC
Sudut ACB = 180 – 60 – 48,59
Sudut ACB = 71,41 derajat
Jadi, sudut ACB memiliki ukuran sebesar 71,41 derajat.
2. Mencari Sudut dengan Menggunakan Teorema Pythagoras:
– Teorema Pythagoras adalah sebuah rumus matematika yang menghubungkan antara panjang sisi miring segitiga dengan panjang sisi-segi dua yang membentuk segitiga tersebut.
– Dengan menggunakan teorema Pythagoras, kita dapat mencari nilai sudut segitiga dengan mengetahui panjang sisi-sisi segitiga.
– Rumus untuk mencari panjang sisi miring (c) adalah sebagai berikut:
c = akar (a^2 + b^2)
– Setelah mengetahui panjang sisi miring, kita dapat mencari nilai sudut segitiga dengan menggunakan sin, cos, atau tan.
Contoh Soal:
Diketahui sebuah segitiga ABC dengan panjang sisi AB = 5 cm, sisi BC = 12 cm, dan sisi AC = 13 cm. Tentukanlah ukuran sudut BAC.
Penyelesaian:
Pertama-tama, kita perlu menentukan panjang sisi miring (c) dengan menggunakan teorema Pythagoras.
c = akar (a^2 + b^2)
c = akar (5^2 + 12^2)
c = akar (169)
c = 13
Setelah mengetahui panjang sisi miring, kita dapat mencari nilai sudut BAC dengan menggunakan fungsi sin.
Sin (BAC) = (sisi yang bersebrangan dengan sudut BAC) / (panjang sisi miring)
Sin (BAC) = (5) / (13)
Sin (BAC) = 0,38
Kita dapat mencari nilai sudut BAC dengan menggunakan tabel trigonometri atau alat kalkulator.
Sin-1 (0,38) = 22,62 derajat
Jadi, sudut BAC memiliki ukuran sebesar 22,62 derajat.
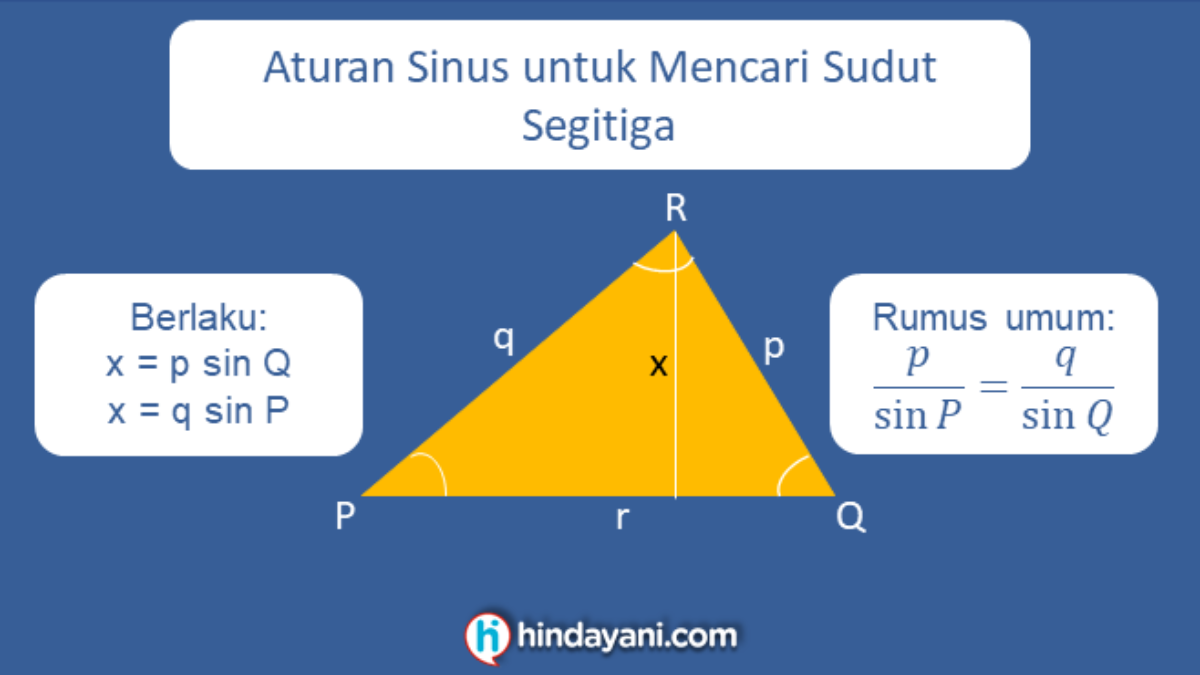
3. Mencari Sudut dengan Menggunakan Rumus Sines:
– Rumus sines adalah sebuah rumus matematika yang menghubungkan antara panjang sisi segitiga dengan sudut yang membentuk segitiga tersebut.
– Dengan menggunakan rumus sines, kita dapat mencari nilai sudut segitiga dengan mengetahui panjang sisi-sisi segitiga.
– Rumus untuk mencari sudut segitiga adalah sebagai berikut:
sin A / a = sin B / b = sin C / c
– Dalam rumus di atas, A, B, dan C adalah sudut-sudut segitiga, sedangkan a, b, dan c adalah panjang sisi-sisi segitiga.
Contoh Soal:
Diketahui sebuah segitiga ABC dengan panjang sisi AB = 8 cm, sisi BC = 10 cm, dan sisi AC = 12 cm. Tentukanlah ukuran sudut BAC.
Penyelesaian:
Pertama-tama, kita perlu menentukan nilai sin (BAC) dengan menggunakan rumus sines.
sin A / a = sin B / b = sin C / c
sin (BAC) / 8 = sin (BCA) / 10 = sin (ABC) / 12
sin (BAC) / 8 = sin (90 derajat) / 10 = sin (ABC) / 12
sin (BAC) / 8 = 1 / 10
sin (BAC) = 0,8
Kita dapat mencari nilai sudut BAC dengan menggunakan tabel trigonometri atau alat kalkulator.
Sin-1 (0,8) = 53,13 derajat
Jadi, sudut BAC memiliki ukuran sebesar 53,13 derajat.
Kesimpulan:
Mencari sudut segitiga merupakan salah satu konsep dasar dalam geometri. Terdapat beberapa cara yang dapat digunakan untuk mencari sudut segitiga, seperti menggunakan trigonometri, teorema Pythagoras, atau rumus sines. Dalam memecahkan masalah, kita perlu memastikan bahwa kita mengetahui nilai dari dua sisi segitiga dan satu sudut yang membentuk segitiga tersebut. Dengan memahami cara mencari sudut segitiga, kita dapat menjawab berbagai soal yang berkaitan dengan sudut segitiga dengan mudah dan cepat.
