Daftar Isi
Luas Tabung Rumus: Pengenalan
Luas tabung adalah hal yang penting untuk dipelajari dalam matematika. Luas tabung merupakan ukuran luas permukaan tabung yang dapat dihitung dengan menggunakan rumus tertentu. Rumus untuk menghitung luas tabung ini dinamakan dengan rumus luas tabung atau rumus tabung.
Dalam matematika, kita sering belajar tentang berbagai macam bentuk dan ukuran. Salah satu bentuk yang paling banyak ditemui adalah tabung. Tabung adalah bentuk tiga dimensi yang terdiri dari sebuah lingkaran dan sebuah silinder yang terhubung di atasnya.
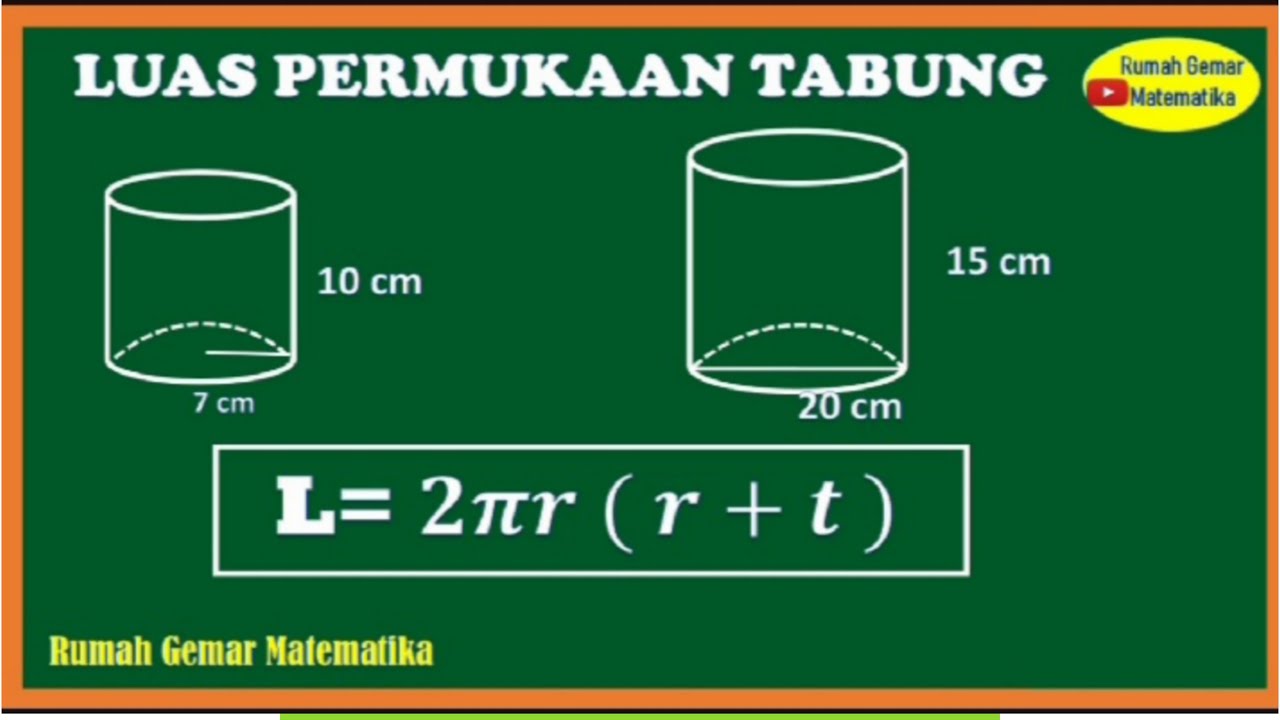
Saat kita berbicara tentang luas permukaan tabung, kita mengacu pada luas keseluruhan permukaan dari bagian silinder dan lingkaran yang terhubung di atasnya. Luas permukaan tabung ini penting untuk dipahami karena dapat digunakan dalam berbagai macam aplikasi, seperti menghitung kuantitas bahan yang dibutuhkan untuk membuat suatu tabung atau merancang suatu produk.
Rumus luas tabung juga dapat digunakan dalam berbagai macam bidang, seperti sains, teknik, dan arsitektur. Jadi, penting bagi kita untuk mempelajari cara menghitung luas tabung dengan benar menggunakan rumus yang tepat.
Cara Menghitung Luas Tabung
Sebelum kita mulai membahas rumus luas tabung, kita perlu memahami terlebih dahulu cara menghitung luas lingkaran dan luas permukaan silinder.
Untuk menghitung luas lingkaran, kita dapat menggunakan rumus:
Luas Lingkaran = π x r^2
Dimana π (pi) merupakan konstanta matematika dengan nilai kira-kira 3.14, dan r adalah jari-jari lingkaran.
Sedangkan untuk menghitung luas permukaan silinder, kita dapat menggunakan rumus:
Luas Permukaan Silinder = 2 x π x r x t + 2 x Luas Lingkaran
Dimana r adalah jari-jari lingkaran dan t adalah tinggi silinder.
Ketika mempelajari rumus luas tabung, kita dapat memanfaatkan kedua rumus tersebut untuk menghitung luas permukaan tabung secara keseluruhan.
Rumus Luas Tabung
Rumus luas tabung menghitung luas permukaan tabung dengan cara menghitung luas permukaan silinder dan menambahkan luas lingkaran pada bagian atas dan bawah silinder.
Rumus Luas Tabung = 2 x π x r x t + 2 x Luas Lingkaran
Kita dapat memecahkan rumus ini menjadi dua bagian: bagian pertama menghitung luas permukaan silinder, dan bagian kedua menghitung luas lingkaran pada bagian atas dan bawah silinder.
Contoh Soal Menghitung Luas Tabung
Untuk memahami rumus luas tabung dengan lebih baik, berikut adalah beberapa contoh soal yang dapat membantu kita menghitung luas tabung.
Contoh Soal 1
Sebuah tabung memiliki jari-jari 7 cm dan tinggi 14 cm. Hitunglah luas permukaan tabung tersebut.
Penyelesaian
Menggunakan rumus luas tabung:
Luas Tabung = 2 x π x r x t + 2 x Luas Lingkaran
= 2 x π x 7 x 14 + 2 x π x 7^2
= 2 x π x 7 x (14 + 7)
= 2 x π x 7 x 21
= 924.0 cm^2
Jadi, luas permukaan tabung tersebut adalah 924.0 cm^2.
Contoh Soal 2
Sebuah tabung berdiameter 20 cm dan tingginya 40 cm. Hitunglah luas permukaan tabung tersebut.
Penyelesaian
Pertama-tama, kita perlu menghitung jari-jari lingkaran dengan menggunakan rumus:
d = 2r
20 = 2r
r = 10 cm
Selanjutnya, kita dapat menghitung luas permukaan tabung dengan menggunakan rumus luas tabung:
Luas Tabung = 2 x π x r x t + 2 x Luas Lingkaran
= 2 x π x 10 x 40 + 2 x π x 10^2
= 2 x π x 10 x (40 + 10)
= 2 x π x 10 x 50
= 3141.59 cm^2
Jadi, luas permukaan tabung tersebut adalah 3141.59 cm^2.
Contoh Soal 3
Sebuah tabung berdiameter 12 cm dan tingginya 30 cm. Hitunglah luas permukaan tabung tersebut.
Penyelesaian
Pertama-tama, kita perlu menghitung jari-jari lingkaran dengan menggunakan rumus:
d = 2r
12 = 2r
r = 6 cm
Selanjutnya, kita dapat menghitung luas permukaan tabung dengan menggunakan rumus luas tabung:
Luas Tabung = 2 x π x r x t + 2 x Luas Lingkaran
= 2 x π x 6 x 30 + 2 x π x 6^2
= 2 x π x 6 x (30 + 6)
= 2 x π x 6 x 36
= 1357.17 cm^2
Jadi, luas permukaan tabung tersebut adalah 1357.17 cm^2.
Kesimpulan
Luas tabung rumus merupakan salah satu pengenalan penting dalam matematika. Rumus ini sangat membantu kita dalam menghitung luas permukaan tabung yang sering digunakan dalam berbagai macam aplikasi dan bidang. Untuk menghitung luas tabung, kita dapat memecahkan rumusnya menjadi dua bagian: bagian pertama menghitung luas permukaan silinder dan bagian kedua menghitung luas lingkaran pada bagian atas dan bawah silinder. Semoga artikel ini bermanfaat bagi pembaca.
 Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
