Daftar Isi
Cara Menghitung Luas Permukaan Tabung
Tabung adalah benda geometris yang memiliki dua buah lingkaran sebagai alasnya dan sisi-sisi yang membentuk silinder. Luas permukaan tabung adalah jumlah luas seluruh sisi-sisi tabung, termasuk alasnya. Berikut adalah langkah-langkah cara menghitung luas permukaan tabung.
1. Menentukan Jari-jari dan Tinggi Tabung
Langkah pertama yang harus dilakukan adalah menentukan jari-jari dan tinggi tabung. Jari-jari (r) adalah jarak dari titik pusat lingkaran alas ke tepi lingkaran, sedangkan tinggi (t) adalah jarak antara kedua lingkaran alas.
2. Menghitung Luas Alas Tabung
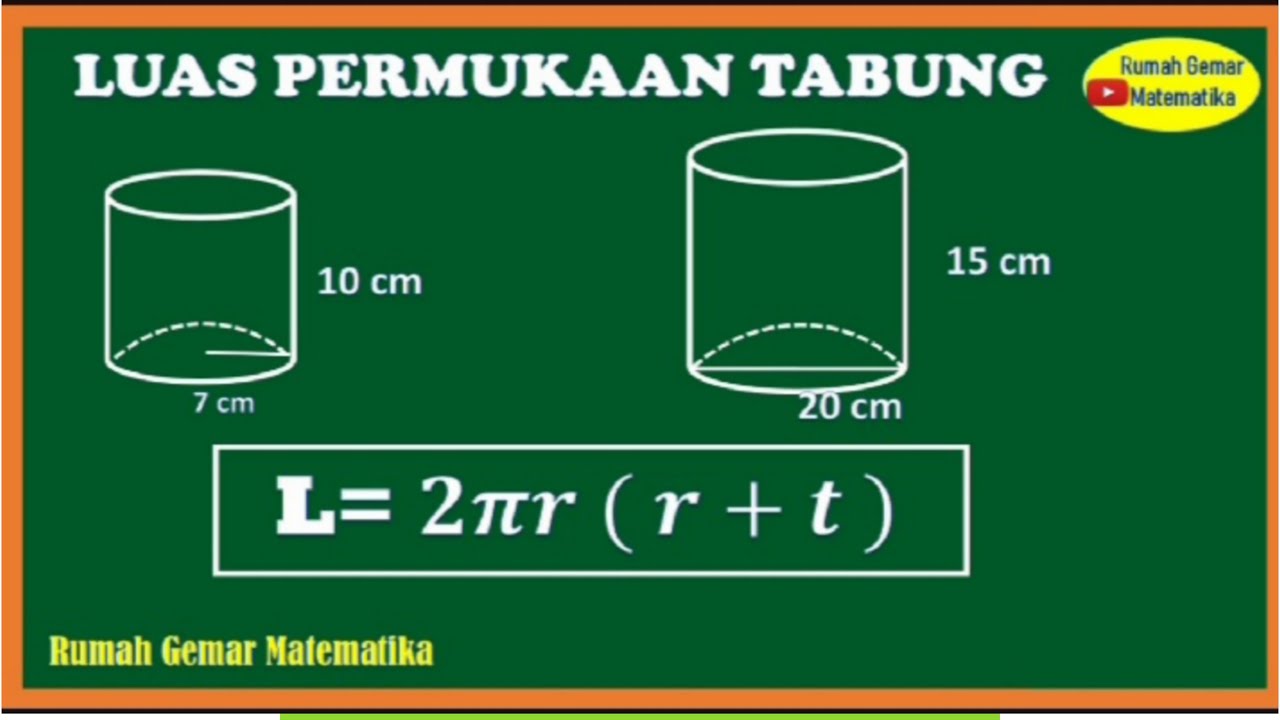
Luas alas tabung dapat dihitung dengan rumus luas lingkaran, yaitu πr². Karena tabung memiliki dua lingkaran sebagai alasnya, maka luas alas tabung adalah 2πr².
3. Menghitung Luas Selimut Tabung
Luas selimut tabung dapat dihitung dengan rumus keliling lingkaran dikali tinggi (K x t), atau juga dapat menggunakan rumus luas permukaan selimut tabung, yaitu 2πrt.
4. Menghitung Luas Permukaan Tabung
Setelah mengetahui luas alas dan luas selimut tabung, langkah selanjutnya adalah menghitung luas permukaan tabung. Luas permukaan tabung dapat dihitung dengan menjumlahkan luas alas dan luas selimut tabung, sehingga rumusnya adalah:
Luas Permukaan Tabung = 2πr² + 2πrt
Contoh Soal:
Sebuah tabung memiliki jari-jari 7 cm dan tinggi 10 cm. Hitunglah luas permukaan tabung tersebut.
Jawab:
Diketahui:
r = 7 cm
t = 10 cm
Langkah 1: Menentukan Luas Alas Tabung
Luas Alas = 2πr²
Luas Alas = 2 x 22/7 x 7²
Luas Alas = 2 x 22/7 x 49
Luas Alas = 308 cm²
Langkah 2: Menentukan Luas Selimut Tabung
Luas Selimut = 2πrt
Luas Selimut = 2 x 22/7 x 7 x 10
Luas Selimut = 2 x 22/7 x 70
Luas Selimut = 440 cm²
Langkah 3: Menentukan Luas Permukaan Tabung
Luas Permukaan Tabung = 2πr² + 2πrt
Luas Permukaan Tabung = 2 x 22/7 x 7² + 2 x 22/7 x 7 x 10
Luas Permukaan Tabung = 2 x 22/7 x 49 + 2 x 22/7 x 70
Luas Permukaan Tabung = 308 + 440
Luas Permukaan Tabung = 748 cm²
Jadi, luas permukaan tabung tersebut adalah 748 cm².
 Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
