Daftar Isi
Pengertian Luas Permukaan Bangun
Luas permukaan bangun adalah ukuran luas yang digunakan untuk mengukur seluruh luas dari permukaan bangun tersebut. Luas permukaan bangun dapat dihitung dengan menggunakan rumus yang berbeda-beda tergantung pada jenis bangun yang dihitung. Istilah luas permukaan bangun biasanya digunakan dalam matematika dan fisika. Dalam matematika, luas permukaan bangun digunakan untuk menghitung luas permukaan dari berbagai macam bangun seperti kubus, balok, tabung, kerucut, bola dan lain sebagainya. Sedangkan dalam fisika, luas permukaan bangun digunakan untuk menghitung luas permukaan dari berbagai macam benda atau objek yang memiliki bentuk yang berbeda-beda.
Rumus Luas Permukaan Bangun
Rumus luas permukaan bangun adalah rumus yang digunakan untuk menghitung luas permukaan dari berbagai macam bangun. Berikut ini adalah rumus luas permukaan dari beberapa bangun yang umum digunakan:
1. Luas Permukaan Kubus
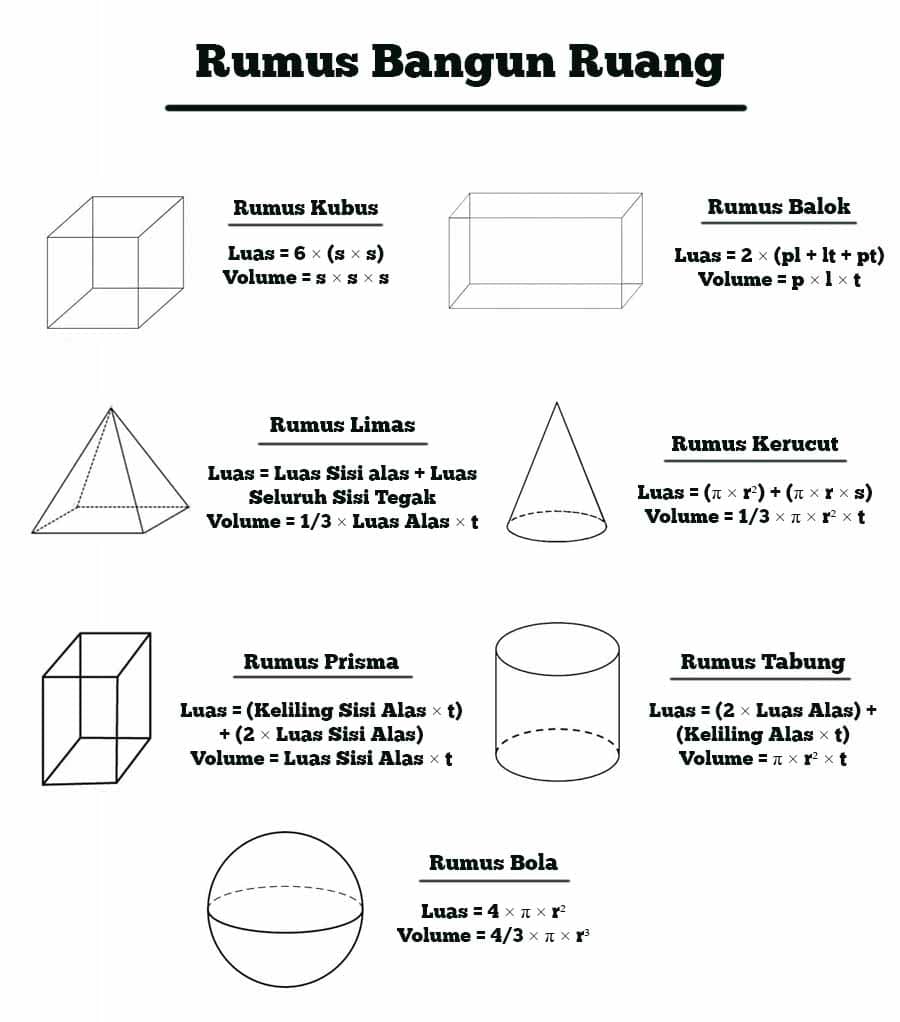
Kubus adalah bangun tiga dimensi yang memiliki enam sisi yang sama besar dan sama panjang. Untuk menghitung luas permukaan kubus, kita dapat menggunakan rumus:
L = 6s²
Keterangan:
L = luas permukaan kubus
s = panjang salah satu sisi kubus
Contoh Soal:
Sebuah kubus memiliki panjang sisi 10 cm. Tentukanlah luas permukaan kubus tersebut!
Penyelesaian:
L = 6s²
L = 6 x 10²
L = 600 cm²
Jadi, luas permukaan kubus tersebut adalah 600 cm².
2. Luas Permukaan Balok
Balok adalah bangun tiga dimensi yang memiliki enam sisi, terdiri dari tiga pasang sisi yang sama panjang dan sama besar. Untuk menghitung luas permukaan balok, kita dapat menggunakan rumus:
L = 2(ab + ac + bc)
Keterangan:
L = luas permukaan balok
a = panjang balok
b = lebar balok
c = tinggi balok
Contoh Soal:
Sebuah balok memiliki panjang 12 cm, lebar 8 cm dan tinggi 6 cm. Tentukanlah luas permukaan balok tersebut!
Penyelesaian:
L = 2(ab + ac + bc)
L = 2(12 x 8 + 12 x 6 + 8 x 6)
L = 2(96 + 72 + 48)
L = 2(216)
L = 432 cm²
Jadi, luas permukaan balok tersebut adalah 432 cm².
3. Luas Permukaan Tabung
Tabung adalah bangun tiga dimensi yang terdiri dari dua lingkaran identik dan satu sisi silinder. Untuk menghitung luas permukaan tabung, kita dapat menggunakan rumus:
L = 2πr² + 2πrh
Keterangan:
L = luas permukaan tabung
r = jari-jari lingkaran tabung
h = tinggi tabung
Contoh Soal:
Sebuah tabung memiliki jari-jari 7 cm dan tinggi 10 cm. Tentukanlah luas permukaan tabung tersebut!
Penyelesaian:
L = 2πr² + 2πrh
L = 2π(7)² + 2π(7)(10)
L = 2π(49) + 2π(70)
L = 98π + 140π
L = 238π
L = 748,08 cm²
Jadi, luas permukaan tabung tersebut adalah 748,08 cm².
4. Luas Permukaan Kerucut
Kerucut adalah bangun tiga dimensi yang terdiri dari satu lingkaran dan satu sisi kerucut. Untuk menghitung luas permukaan kerucut, kita dapat menggunakan rumus:
L = πr² + πrl
Keterangan:
L = luas permukaan kerucut
r = jari-jari lingkaran kerucut
l = garis pelukis kerucut
Contoh Soal:
Sebuah kerucut memiliki jari-jari 6 cm dan garis pelukis 10 cm. Tentukanlah luas permukaan kerucut tersebut!
Penyelesaian:
L = πr² + πrl
L = π(6)² + π(6)(10)
L = π(36) + π(60)
L = 36π + 60π
L = 96π
L = 301,59 cm²
Jadi, luas permukaan kerucut tersebut adalah 301,59 cm².
5. Luas Permukaan Bola
Bola adalah bangun tiga dimensi yang terdiri dari satu lingkaran yang diputar pada sumbu lingkaran. Untuk menghitung luas permukaan bola, kita dapat menggunakan rumus:
L = 4πr²
Keterangan:
L = luas permukaan bola
r = jari-jari bola
Contoh Soal:
Sebuah bola memiliki jari-jari 5 cm. Tentukanlah luas permukaan bola tersebut!
Penyelesaian:
L = 4πr²
L = 4π(5)²
L = 4π(25)
L = 100π
L = 314,16 cm²
Jadi, luas permukaan bola tersebut adalah 314,16 cm².
Cara Menghitung Luas Permukaan Bangun
Menghitung luas permukaan bangun dapat dilakukan dengan mudah jika kita sudah memahami rumus-rumus yang digunakan untuk setiap jenis bangun. Berikut ini adalah langkah-langkah cara menghitung luas permukaan bangun:
1. Tentukan jenis bangun yang akan dihitung
Langkah pertama yang harus dilakukan adalah menentukan jenis bangun yang akan dihitung. Setiap jenis bangun memiliki rumus yang berbeda-beda sehingga kita harus memahami rumus tersebut terlebih dahulu sebelum menghitung luas permukaan.
2. Tentukan nilai-nilai yang diketahui
Setelah mengetahui jenis bangun yang akan dihitung, langkah selanjutnya adalah menentukan nilai-nilai yang diketahui. Nilai-nilai yang diketahui biasanya terdiri dari panjang, lebar, tinggi, jari-jari dan garis pelukis.
3. Masukkan nilai-nilai ke dalam rumus
Setelah menentukan nilai-nilai yang diketahui, langkah selanjutnya adalah memasukkan nilai-nilai tersebut ke dalam rumus yang sesuai dengan jenis bangun yang dihitung.
4. Hitung hasilnya
Setelah memasukkan nilai-nilai ke dalam rumus, langkah terakhir adalah menghitung hasilnya. Hasil yang didapatkan biasanya dalam satuan luas seperti cm², m² atau in².
Contoh Soal dan Pembahasan Luas Permukaan Bangun
Untuk memahami lebih lanjut mengenai cara menghitung luas permukaan bangun, berikut ini akan dibahas contoh soal dan pembahasannya:
Contoh Soal 1:
Sebuah balok memiliki panjang 10 cm, lebar 6 cm dan tinggi 8 cm. Tentukanlah luas permukaan balok tersebut!
Pembahasan:
L = 2(ab + ac + bc)
L = 2(10 x 6 + 10 x 8 + 6 x 8)
L = 2(60 + 80 + 48)
L = 2(188)
L = 376 cm²
Jadi, luas permukaan balok tersebut adalah 376 cm².
Contoh Soal 2:
Sebuah tabung memiliki jari-jari 5 cm dan tinggi 12 cm. Tentukanlah luas permukaan tabung tersebut!
Pembahasan:
L = 2πr² + 2πrh
L = 2π(5)² + 2π(5)(12)
L = 2π(25) + 2π(60)
L = 50π + 120π
L = 170π
L = 534,07 cm²
Jadi, luas permukaan tab
 Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
