Deret Aritmatika dan Geometri

Deret adalah sebuah urutan bilangan yang tersusun secara berurutan. Ada dua jenis deret yaitu deret aritmatika dan deret geometri. Dalam matematika, deret aritmatika dan geometri sangat penting karena sering digunakan dalam berbagai macam perhitungan.

Deret Aritmatika

Deret aritmatika adalah deret yang setiap bilangannya bertambah dengan suatu bilangan tetap yang disebut beda (d). Dalam deret aritmatika, setiap suku (an) berhubungan dengan suku sebelumnya (an-1) dengan rumus berikut:

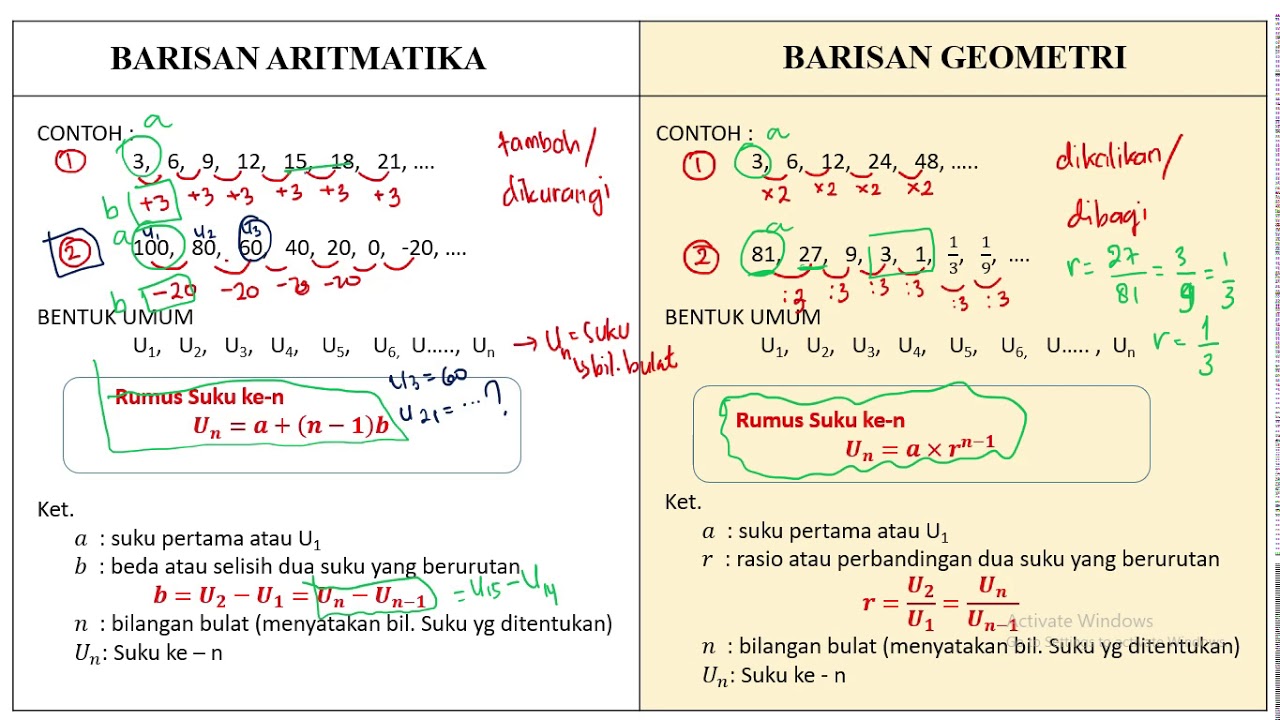
an = an-1 + d

Contohnya adalah sebagai berikut:

2, 4, 6, 8, 10, 12, …

Beda (d) dari deret ini adalah 2 karena setiap suku bertambah 2 dari suku sebelumnya. Jadi, rumus umum untuk deret aritmatika adalah sebagai berikut:

an = a1 + (n-1)d

Di mana an adalah suku ke-n, a1 adalah suku pertama, n adalah jumlah suku, dan d adalah beda.

Contoh perhitungan deret aritmatika:

Tentukan jumlah 10 suku pertama dari deret aritmatika dengan suku pertama (a1) 3 dan beda (d) 2.

Penyelesaian:

Kita akan menggunakan rumus untuk menjumlahkan deret aritmatika:

Sn = n/2 (a1 + an)

Dalam kasus ini, a1 = 3, d = 2, dan n = 10. Mari kita cari an terlebih dahulu:

an = a1 + (n-1)d
an = 3 + (10-1)2
an = 3 + 18
an = 21

Sekarang kita dapat menghitung jumlah 10 suku pertama:

Sn = n/2 (a1 + an)
Sn = 10/2 (3 + 21)
Sn = 5 (24)
Sn = 120

Jadi, jumlah 10 suku pertama dari deret ini adalah 120.

Deret Geometri

Deret geometri adalah deret yang setiap bilangannya dikalikan dengan suatu bilangan tetap yang disebut rasio (r). Dalam deret geometri, setiap suku (an) berhubungan dengan suku sebelumnya (an-1) dengan rumus berikut:

an = an-1 x r

Contohnya adalah sebagai berikut:

2, 4, 8, 16, 32, …

Rasio (r) dari deret ini adalah 2 karena setiap suku dikalikan dengan 2 dari suku sebelumnya. Jadi, rumus umum untuk deret geometri adalah sebagai berikut:

an = a1 x r^(n-1)

Di mana an adalah suku ke-n, a1 adalah suku pertama, n adalah jumlah suku, dan r adalah rasio.

Contoh perhitungan deret geometri:

Tentukan jumlah 8 suku pertama dari deret geometri dengan suku pertama (a1) 2 dan rasio (r) 3.

Penyelesaian:

Kita akan menggunakan rumus untuk menjumlahkan deret geometri:

Sn = a1 (1 – r^n) / (1 – r)

Dalam kasus ini, a1 = 2, r = 3, dan n = 8. Mari kita hitung jumlah 8 suku pertama:

Sn = a1 (1 – r^n) / (1 – r)
Sn = 2 (1 – 3^8) / (1 – 3)
Sn = 2 (-6561) / (-2)
Sn = 6562

Jadi, jumlah 8 suku pertama dari deret ini adalah 6562.

Perbedaan Antara Deret Aritmatika dan Geometri

Kedua deret tersebut memiliki perbedaan yang mencolok. Pada deret aritmatika, setiap suku bertambah dengan suatu bilangan tetap (beda), sedangkan pada deret geometri, setiap suku dikalikan dengan suatu bilangan tetap (rasio). Selain itu, rumus umum untuk masing-masing deret juga berbeda.

Dalam deret aritmatika, jumlahan suku-suku yang muncul bersifat linear, yaitu bergerak dalam satu arah. Sedangkan pada deret geometri, jumlahan suku muncul secara eksponensial, yaitu bergerak lebih cepat dari satu arah.

Kedua deret ini juga memiliki kegunaan praktis dalam kehidupan sehari-hari. Misalnya, ketika memperkirakan hasil investasi pada beberapa tahun mendatang, kita dapat menggunakan deret geometri. Sedangkan ketika menghitung berapa banyak uang yang akan diperoleh setiap bulan selama kurun waktu tertentu, kita dapat menggunakan deret aritmatika.

Contoh Soal

Berikut adalah beberapa contoh soal mengenai deret aritmatika dan geometri:

1. Tentukan suku ke-15 dari deret aritmatika dengan suku pertama (a1) 10 dan beda (d) 6.

Penyelesaian:

Kita menggunakan rumus umum deret aritmatika:

an = a1 + (n-1)d

Dalam kasus ini, a1 = 10, d = 6, dan n = 15. Mari kita cari an:

an = a1 + (n-1)d
an = 10 + (15-1)6
an = 10 + 84
an = 94

Jadi, suku ke-15 dari deret ini adalah 94.

2. Tentukan jumlah 12 suku pertama dari deret geometri dengan suku pertama (a1) 3 dan rasio (r) 2.

Penyelesaian:

Kita menggunakan rumus umum deret geometri:

Sn = a1 (1 – r^n) / (1 – r)

Dalam kasus ini, a1 = 3, r = 2, dan n = 12. Mari kita cari jumlah 12 suku pertama:

Sn = a1 (1 – r^n) / (1 – r)
Sn = 3 (1 – 2^12) / (1 – 2)
Sn = 3 (-4095) / (-1)
Sn = 12285

Jadi, jumlah 12 suku pertama dari deret ini adalah 12285.

3. Tentukan beda (d) dari deret aritmatika dengan suku pertama (a1) 7 dan suku ke-10 28.

Penyelesaian:

Kita menggunakan rumus umum deret aritmatika:

an = a1 + (n-1)d

Dalam kasus ini, a1 = 7, an = 28, dan n = 10. Mari kita cari d:

an = a1 + (n-1)d
28 = 7 + (10-1)d
28 = 7 + 9d
d = 3

Jadi, beda (d) dari deret ini adalah 3.

4. Tentukan suku ke-7 dari deret geometri dengan suku pertama (a1) 5 dan rasio (r) 4.

Penyelesaian:

Kita menggunakan rumus umum deret geometri:

an = a1 x r^(n-1)

Dalam kasus ini, a1 = 5, r = 4, dan n = 7. Mari kita cari an:

an = a1 x r^(n-1)
an = 5 x 4^(7-1)
an = 5 x 4^6
an = 5120

Jadi, suku ke-7 dari deret ini adalah 5120.

Kesimpulan

Deret aritmatika dan geometri adalah konsep matematika yang sangat penting dalam berbagai macam perhitungan. Kedua deret tersebut memiliki rumus umum yang berbeda, serta perbedaan dalam cara bilangan-bilangannya berhubungan satu sama lain. Dalam kehidupan sehari-hari, kedua deret ini sering digunakan dalam berbagai macam perhitungan, seperti investasi atau perencanaan keuangan. Dengan memahami konsep deret aritmatika dan geometri, kita dapat menggunakannya secara efektif dalam berbagai macam situasi.