Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Daftar Isi
Pengertian Barisan Aritmatika
Barisan aritmatika adalah suatu deret bilangan yang setiap suku atau elemennya memiliki selisih atau beda yang tetap dan konstan. Beda ini biasa disebut dengan istilah d atau delta. Misalnya, barisan aritmatika dengan suku awal atau pertama a1 dan beda d adalah sebagai berikut:
a1, a1+d, a1+2d, a1+3d, a1+4d, dan seterusnya
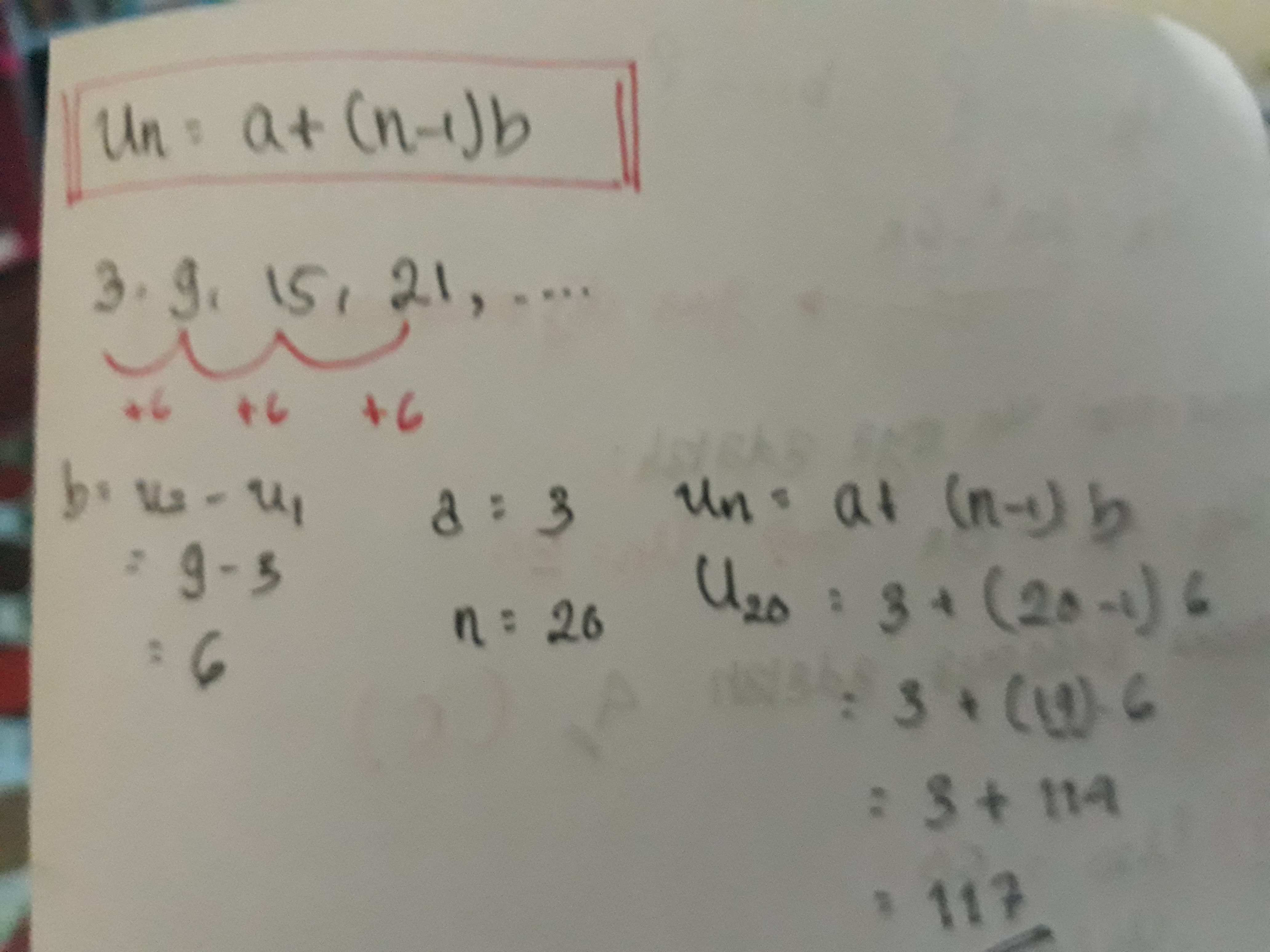
Dalam barisan tersebut, nilai a1 adalah suku pertama, d adalah beda antara setiap dua suku berturut-turut, dan seterusnya. Barisan aritmatika juga bisa diwakili dengan rumus umum sebagai berikut:
an = a1 + (n-1)d
Dimana, an adalah suku ke-n, a1 adalah suku pertama, n adalah indeks atau urutan suku ke-n, dan d adalah beda antara setiap dua suku berturut-turut.
Contoh Soal Barisan Aritmatika SMA
Soal 1. Tentukan suku ke-10 dan suku ke-20 dari barisan aritmatika berikut: 2, 5, 8, 11, …
Penyelesaian:
Dari barisan tersebut, kita dapat menentukan nilai a1 dan beda d sebagai berikut:
a1 = 2
d = 5 – 2 = 3
Untuk mencari suku ke-10, kita gunakan rumus umum sebagai berikut:
a10 = a1 + (10-1)d
a10 = 2 + 9(3)
a10 = 2 + 27
a10 = 29
Jadi, suku ke-10 dari barisan tersebut adalah 29.
Untuk mencari suku ke-20, kita gunakan rumus umum yang sama:
a20 = a1 + (20-1)d
a20 = 2 + 19(3)
a20 = 2 + 57
a20 = 59
Jadi, suku ke-20 dari barisan tersebut adalah 59.
Soal 2. Jumlahkan 10 suku pertama dari barisan aritmatika berikut: 7, 13, 19, 25, …
Penyelesaian:
Dari barisan tersebut, kita dapat menentukan nilai a1 dan beda d sebagai berikut:
a1 = 7
d = 13 – 7 = 6
Untuk mencari jumlah 10 suku pertama, kita gunakan rumus jumlah suku pertama pada barisan aritmatika sebagai berikut:
Sn = n/2 (2a1 + (n-1)d)
Substitusikan n = 10, a1 = 7, dan d = 6 ke dalam rumus di atas:
S10 = 10/2 (2(7) + (10-1)(6))
S10 = 5(14 + 54)
S10 = 5(68)
S10 = 340
Jadi, jumlah 10 suku pertama dari barisan tersebut adalah 340.
Soal 3. Tentukan suku ke-n dari barisan aritmatika berikut: 3, 7, 11, 15, …
Penyelesaian:
Dari barisan tersebut, kita dapat menentukan nilai a1 dan beda d sebagai berikut:
a1 = 3
d = 7 – 3 = 4
Untuk mencari suku ke-n, kita gunakan rumus umum sebagai berikut:
an = a1 + (n-1)d
Namun, kita tidak tahu nilai n atau indeks suku yang ingin dicari. Oleh karena itu, kita perlu mencari terlebih dahulu nilai n dari suku ke-n tersebut.
Dalam hal ini, kita perlu mencari selisih atau beda antara suku ke-n dengan suku pertama a1. Misalnya, jika kita ingin mencari suku ke-10, maka selisihnya dengan suku pertama adalah:
10 – 1 = 9
Dalam hal ini, selisih atau beda tersebut adalah 9. Kita dapat mengganti nilai n dengan selisih atau beda tersebut, sehingga:
an = a1 + (n-1)d
an = a1 + (9)d
an = 3 + 9(4)
an = 3 + 36
an = 39
Jadi, suku ke-10 dari barisan tersebut adalah 39.
Soal 4. Tentukan suku ke-n dari barisan aritmatika berikut: -2, 1, 4, 7, …
Penyelesaian:
Dari barisan tersebut, kita dapat menentukan nilai a1 dan beda d sebagai berikut:
a1 = -2
d = 1 – (-2) = 3
Untuk mencari suku ke-n, kita gunakan rumus umum sebagai berikut:
an = a1 + (n-1)d
Namun, kita tidak tahu nilai n atau indeks suku yang ingin dicari. Oleh karena itu, kita perlu mencari terlebih dahulu nilai n dari suku ke-n tersebut.
Dalam hal ini, kita perlu mencari selisih atau beda antara suku ke-n dengan suku pertama a1. Misalnya, jika kita ingin mencari suku ke-20, maka selisihnya dengan suku pertama adalah:
20 – 1 = 19
Dalam hal ini, selisih atau beda tersebut adalah 19. Kita dapat mengganti nilai n dengan selisih atau beda tersebut, sehingga:
an = a1 + (n-1)d
an = a1 + (19)d
an = -2 + 19(3)
an = -2 + 57
an = 55
Jadi, suku ke-20 dari barisan tersebut adalah 55.
Soal 5. Tentukan suku yang hilang dari barisan aritmatika berikut: 3, 7, __, 15, 19, …
Penyelesaian:
Dari barisan tersebut, kita dapat menentukan nilai a1 dan beda d sebagai berikut:
a1 = 3
d = 7 – 3 = 4
Untuk mencari suku yang hilang, kita perlu mencari selisih atau beda antara suku yang diberikan. Misalnya, selisih antara suku kedua dan ketiga adalah:
7 – x = x – 3
2x = 10
x = 5
Dalam hal ini, suku yang hilang adalah 5.
Jadi, barisan aritmatika tersebut adalah: 3, 7, 5, 15, 19, …
Kesimpulan
Barisan aritmatika adalah suatu deret bilangan yang setiap suku atau elemennya memiliki selisih atau beda yang tetap dan konstan. Beda ini biasa disebut dengan istilah d atau delta. Untuk menyelesaikan soal-soal barisan aritmatika, kita perlu menentukan nilai a1 dan beda d terlebih dahulu, kemudian menggunakan rumus umum atau rumus jumlah suku pertama pada barisan aritmatika. Dalam beberapa kasus, kita juga perlu mencari nilai n atau indeks suku yang ingin dicari terlebih dahulu.
