Cara Menghitung Pembagian Yang Tepat Dan Akurat

Cara Menghitung Pembagian: Konsep Dasar dan Langkah-Langkah

Pembagian merupakan salah satu operasi matematika dasar yang sering digunakan dalam kehidupan sehari-hari. Pada dasarnya, pembagian adalah proses membagi suatu bilangan dengan bilangan lainnya untuk mendapatkan hasil pembagian atau quotient. Dalam artikel ini, akan dijelaskan konsep dasar pembagian serta langkah-langkah cara menghitung pembagian dengan tepat.

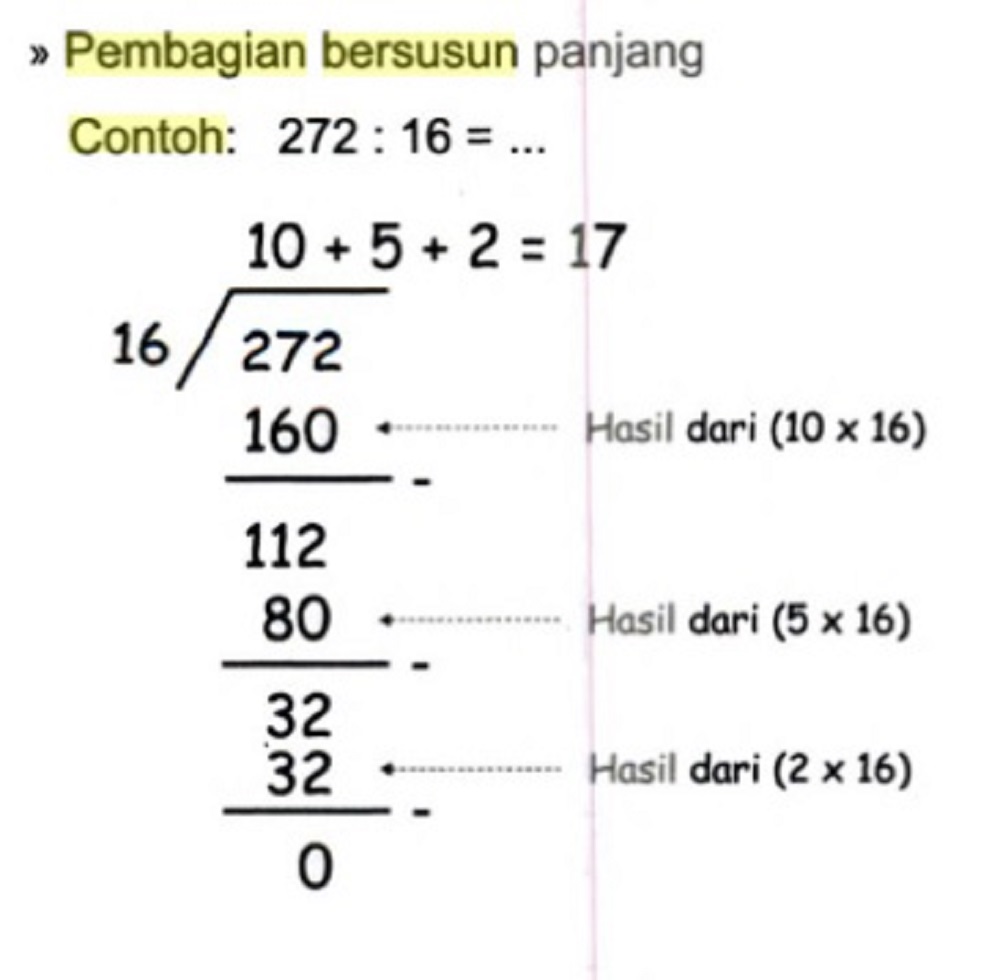
Konsep Dasar Pembagian

Dalam matematika, pembagian memiliki dua istilah penting, yaitu:

1. Dividen: Bilangan yang akan dibagi atau dipecahkan menjadi beberapa bagian.

2. Pembagi: Bilangan yang digunakan untuk membagi atau memecahkan dividen menjadi beberapa bagian yang sama besar.

Hasil pembagian disebut sebagai quotient atau hasil bagi. Dalam operasi pembagian, terdapat dua jenis bilangan, yaitu:

1. Bilangan bulat atau integer: Bilangan yang tidak mengandung pecahan.

2. Bilangan pecahan atau desimal: Bilangan yang mengandung pecahan.

Dalam pembagian bilangan bulat, hasil pembagian dapat berupa bilangan bulat atau pecahan. Namun, pada pembagian bilangan pecahan, hasil pembagian selalu berupa bilangan pecahan.

Langkah-Langkah Cara Menghitung Pembagian

Berikut ini adalah langkah-langkah cara menghitung pembagian yang perlu diperhatikan:

1. Pastikan bilangan yang akan dibagi (dividen) dan bilangan pembagi (pembagi) telah diketahui.

2. Tentukan hasil pembagian yang diinginkan atau quotient.

3. Bagi bilangan pembagi dengan bilangan dividen. Jika bilangan pembagi lebih besar dari bilangan dividen, maka hasil pembagian akan selalu berupa bilangan pecahan.

4. Lakukan pembagian dengan menggunakan metode pembagian berulang atau metode matematika dasar lainnya. Pada metode pembagian berulang, langkah-langkahnya adalah:

a. Tuliskan bilangan pembagi dan dividen dalam baris vertikal.

b. Bagi bilangan pembagi dengan digit pertama dari bilangan dividen.

c. Tuliskan hasil pembagian pada baris di bawah bilangan pembagi dan digit pertama dividen.

d. Kalikan hasil pembagian dengan digit pertama dividen.

e. Kurangkan hasil kali tersebut dari digit pertama dividen untuk mendapatkan sisa.

f. Tambahkan digit kedua bilangan dividen ke sisa untuk membentuk bilangan sisa baru.

g. Lakukan kembali pembagian dengan bilangan sisa baru sebagai digit pertama bilangan dividen.

h. Ulangi langkah-langkah di atas hingga tidak ada lagi digit bilangan dividen yang tersisa.

i. Tuliskan hasil pembagian yang diperoleh sebagai quotient.

Contoh Perhitungan Pembagian

Berikut ini adalah beberapa contoh perhitungan pembagian menggunakan metode pembagian berulang:

Contoh 1: Hitunglah 48 dibagi dengan 6.

Langkah 1: Pastikan bilangan yang akan dibagi dan bilangan pembagi telah diketahui, yaitu 48 dan 6.

Langkah 2: Tentukan hasil pembagian yang diinginkan atau quotient.

Langkah 3: Bagi bilangan pembagi dengan bilangan dividen.

Langkah 4: Lakukan pembagian dengan menggunakan metode pembagian berulang.

6)48
– 6
—
18
-12
—
6

Hasil pembagian adalah 8.

Contoh 2: Hitunglah 25 dibagi dengan 4.

Langkah 1: Pastikan bilangan yang akan dibagi dan bilangan pembagi telah diketahui, yaitu 25 dan 4.

Langkah 2: Tentukan hasil pembagian yang diinginkan atau quotient.

Langkah 3: Bagi bilangan pembagi dengan bilangan dividen.

Langkah 4: Lakukan pembagian dengan menggunakan metode pembagian berulang.

4)25
– 4
—
21
-20
—
1

Hasil pembagian adalah 6 1/4 atau 6,25.

Contoh 3: Hitunglah 93 dibagi dengan 7.

Langkah 1: Pastikan bilangan yang akan dibagi dan bilangan pembagi telah diketahui, yaitu 93 dan 7.

Langkah 2: Tentukan hasil pembagian yang diinginkan atau quotient.

Langkah 3: Bagi bilangan pembagi dengan bilangan dividen.

Langkah 4: Lakukan pembagian dengan menggunakan metode pembagian berulang.

7)93
– 7
—
26
-21
—
5

Hasil pembagian adalah 13 5/7 atau 13,57.

Kesimpulan

Pembagian merupakan salah satu operasi matematika dasar yang sangat penting dalam kehidupan sehari-hari. Dalam pembagian, terdapat konsep dasar dan langkah-langkah yang perlu diperhatikan agar hasil pembagian dapat diperoleh dengan tepat. Salah satu metode yang dapat digunakan untuk menghitung pembagian adalah metode pembagian berulang atau metode matematika dasar lainnya. Dengan memahami konsep dasar pembagian dan langkah-langkah cara menghitung pembagian yang tepat, diharapkan pembaca dapat memperoleh hasil pembagian yang akurat dan tepat.