Cara Mencari Sudut Segitiga

Segitiga merupakan bentuk bangun datar yang memiliki tiga sisi dan tiga sudut. Salah satu hal penting yang perlu diketahui dalam pembahasan tentang segitiga adalah cara mencari sudut segitiga. Sudut segitiga merupakan sudut yang terbentuk oleh dua sisi segitiga. Dalam artikel ini akan dibahas cara mencari sudut segitiga beserta contoh soal dan pembahasannya.

1. Menggunakan Teorema Pythagoras

Cara pertama untuk mencari sudut segitiga adalah menggunakan teorema Pythagoras. Teorema Pythagoras menyatakan bahwa pada segitiga siku-siku, kuadrat dari sisi miring sama dengan jumlah kuadrat dari sisi-sisinya. Dalam hal ini, kita akan menggunakan teorema Pythagoras untuk mencari salah satu sudut segitiga.

Langkah-langkahnya adalah sebagai berikut:

– Identifikasi segitiga siku-siku
– Tentukan sisi miring segitiga
– Kuadratkan sisi miring
– Kuadratkan kedua sisi lainnya
– Jumlahkan kuadrat kedua sisi tersebut
– Hitung akar dari jumlah kedua sisi
– Gunakan arctan untuk mencari sudut segitiga

Contoh Soal:
Diketahui segitiga ABC dengan sisi AC = 5 dan sisi AB = 12. Tentukan sudut BAC!

Pembahasan:
Identifikasi terlebih dahulu segitiga ABC apakah segitiga siku-siku atau tidak. Dalam segitiga ABC, sisi AB dan AC adalah sisi-sisi segitiga, sedangkan sisi BC adalah sisi miring. Karena sisi miring segitiga siku-siku selalu berada di samping sudut siku-siku, maka sudut BAC adalah sudut yang akan dicari.

Kuadratkan sisi miring segitiga:
BC^2 = AB^2 + AC^2
BC^2 = 12^2 + 5^2
BC^2 = 144 + 25
BC^2 = 169

Hitung akar dari jumlah kedua sisi:
BC = √169
BC = 13

Gunakan arctan untuk mencari sudut segitiga:
tan(A) = AC/BC
tan(A) = 5/13
A = arctan(5/13)
A = 21,8°

Jadi, sudut BAC adalah 21,8°.

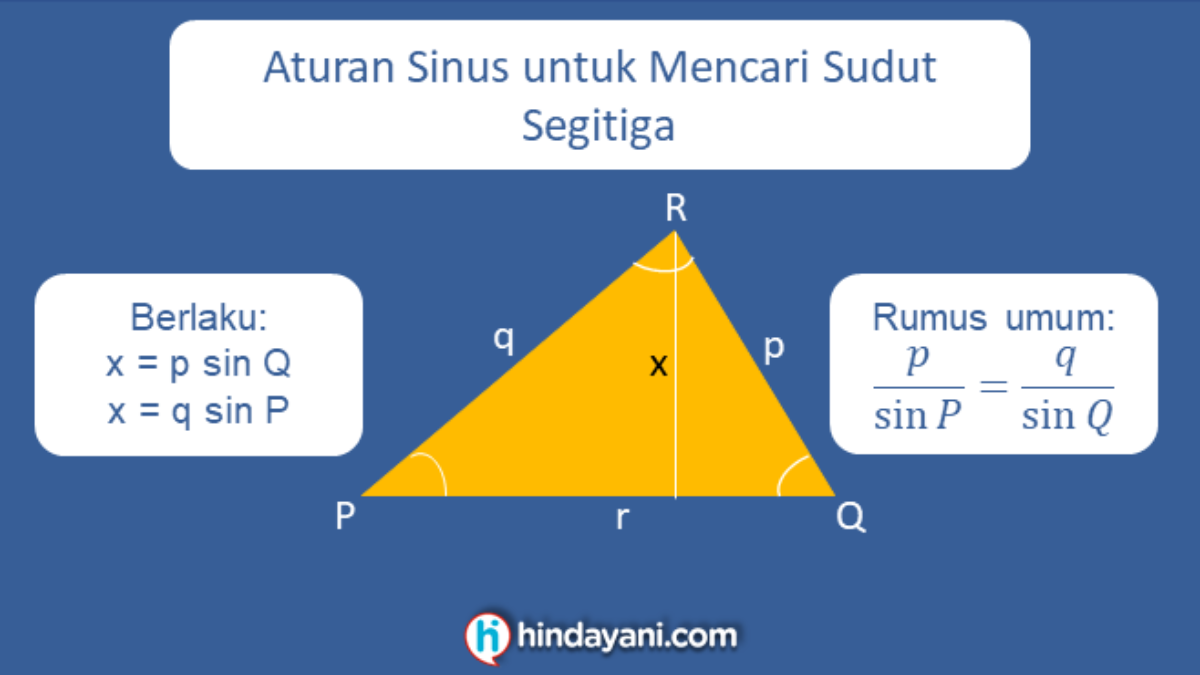
2. Menggunakan Hukum Sinus

Cara kedua untuk mencari sudut segitiga adalah menggunakan hukum sinus. Hukum sinus menyatakan bahwa rasio antara sisi dengan sinus sudut yang berlawanan sama untuk semua sisi dalam segitiga. Dalam hal ini, kita akan menggunakan hukum sinus untuk mencari salah satu sudut segitiga.

Langkah-langkahnya adalah sebagai berikut:

– Tentukan tiga sisi segitiga
– Tentukan satu sudut segitiga yang diketahui
– Gunakan hukum sinus untuk mencari sinus dari sudut yang diketahui
– Hitung sinus dari kedua sudut lainnya
– Gunakan arccos untuk mencari sudut segitiga

Contoh Soal:
Diketahui segitiga ABC dengan sisi AB = 6, sisi AC = 9, dan sudut BAC = 30°. Tentukan sudut ABC dan sudut ACB!

Pembahasan:
Tentukan terlebih dahulu tiga sisi segitiga AB, AC, dan BC. Kemudian, tentukan satu sudut segitiga yang diketahui yaitu sudut BAC.

Gunakan hukum sinus untuk mencari sinus dari sudut BAC:
sin(BAC) = AB/AC
sin(30) = 6/9
sin(30) = 0,6667

Hitung sinus dari sudut ABC:
sin(ABC) = BC/AC x sin(BAC)
sin(ABC) = BC/9 x 0,6667

Hitung sinus dari sudut ACB:
sin(ACB) = AB/BC x sin(BAC)
sin(ACB) = 6/BC x 0,6667

Gunakan arccos untuk mencari sudut segitiga:
cos(ABC) = (sin(ACB) x sin(BAC)) / sin(ABC)
cos(ABC) = (6/BC x 0,6667) / (BC/9 x 0,6667)
cos(ABC) = 0,4

ABC = arccos(0,4)
ABC = 66,4°

ACB = arccos(0,6)
ACB = 49,5°

Jadi, sudut ABC adalah 66,4° dan sudut ACB adalah 49,5°.

3. Menggunakan Hukum Kosinus

Cara ketiga untuk mencari sudut segitiga adalah menggunakan hukum kosinus. Hukum kosinus menyatakan bahwa kuadrat dari sisi miring sama dengan jumlah kuadrat dari kedua sisi yang lain dikurangi dua kali hasil kali kedua sisi tersebut dengan kosinus sudut yang berlawanan. Dalam hal ini, kita akan menggunakan hukum kosinus untuk mencari salah satu sudut segitiga.

Langkah-langkahnya adalah sebagai berikut:

– Tentukan tiga sisi segitiga
– Tentukan sisi miring segitiga
– Hitung kuadrat dari kedua sisi lainnya
– Jumlahkan kedua kuadrat tersebut dan kurangi dengan kuadrat sisi miring
– Bagi hasil kurangan tersebut dengan dua kali hasil kali kedua sisi yang lain
– Hitung akar dari hasil bagi tersebut
– Gunakan arccos untuk mencari sudut segitiga

Contoh Soal:
Diketahui segitiga ABC dengan sisi AB = 6, sisi AC = 9, dan sisi BC = 7. Tentukan sudut BAC!

Pembahasan:
Tentukan terlebih dahulu tiga sisi segitiga AB, AC, dan BC. Kemudian, tentukan sisi miring segitiga yaitu sisi BC.

Hitung kuadrat dari kedua sisi lainnya:
AB^2 = 6^2 = 36
AC^2 = 9^2 = 81

Jumlahkan kedua kuadrat tersebut dan kurangi dengan kuadrat sisi miring:
36 + 81 – 49 = 68

Bagi hasil kurangan tersebut dengan dua kali hasil kali kedua sisi yang lain:
68 / (2 x 6 x 9) = 0,3778

Hitung akar dari hasil bagi tersebut:
√0,3778 = 0,6148

Gunakan arccos untuk mencari sudut segitiga:
cos(BAC) = (AC^2 + AB^2 – BC^2) / 2ABxAC
cos(BAC) = (81 + 36 – 49) / 2x6x9
cos(BAC) = 68 / 108
cos(BAC) = 0,6296

BAC = arccos(0,6296)
BAC = 50,7°

Jadi, sudut BAC adalah 50,7°.

Kesimpulan

Mencari sudut segitiga dapat dilakukan dengan menggunakan beberapa cara seperti teorema Pythagoras, hukum sinus, dan hukum kosinus. Ketiga cara tersebut dapat digunakan tergantung kondisi dan informasi yang diberikan pada soal. Dalam setiap cara yang digunakan, perlu dilakukan identifikasi terhadap segitiga terlebih dahulu untuk memudahkan perhitungan dan pencarian sudut segitiga. Dalam menyelesaikan soal, pastikan perhitungan yang dilakukan berdasarkan rumus yang tepat dan hasilnya sudah diuji kembali oleh kita untuk memastikan kebenaran hasil yang diperoleh.