Daftar Isi
Pengertian Invers Matriks 3×3
Sebelum membahas bagaimana cara mencari invers matriks 3×3, kita perlu memahami terlebih dahulu apa itu invers matriks 3×3. Invers matriks 3×3 adalah matriks yang jika dikalikan dengan matriks asalnya, akan menghasilkan matriks identitas. Matriks identitas adalah matriks persegi dengan diagonal utama yang berisi angka 1 dan elemen lainnya berisi angka 0.
Invers matriks 3×3 sangat berguna dalam berbagai aplikasi matematika, seperti sistem persamaan linear, transformasi linier, dan pengolahan citra. Oleh karena itu, penting untuk mengetahui cara mencari invers matriks 3×3.
Persyaratan Invers Matriks 3×3
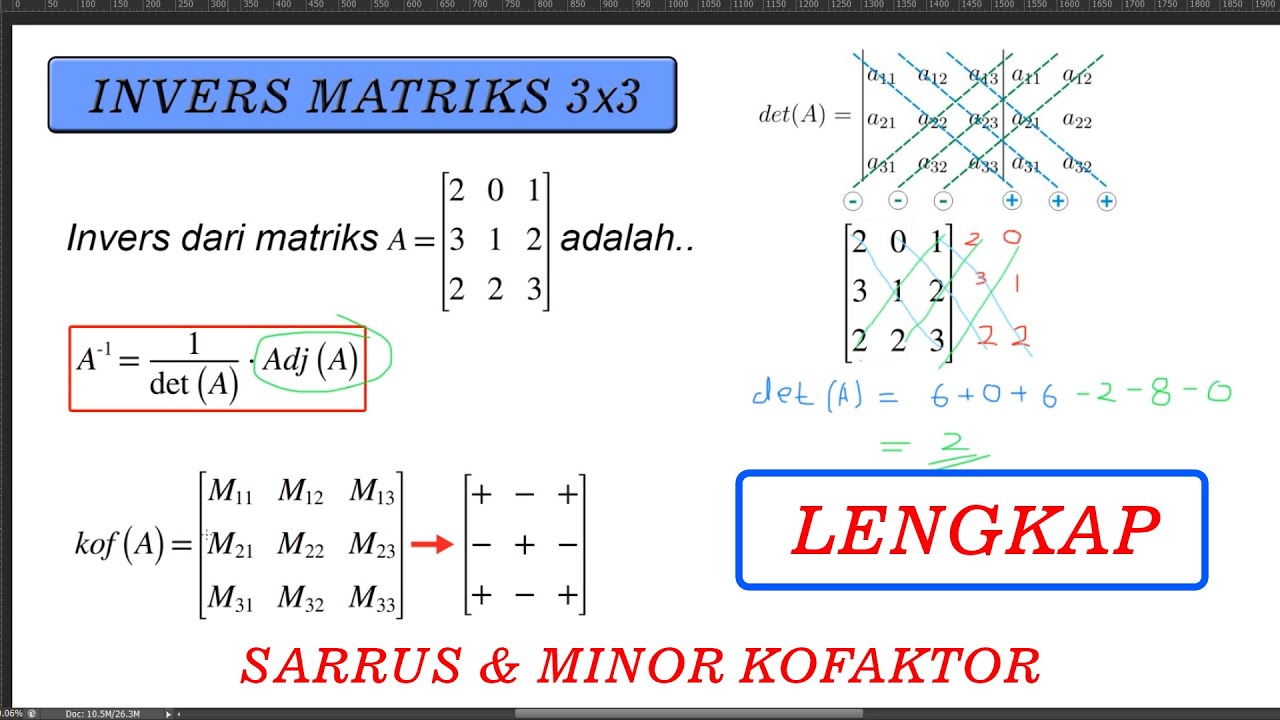
Sebelum mencari invers matriks 3×3, ada beberapa persyaratan yang perlu dipenuhi terlebih dahulu. Pertama, determinan matriks 3×3 harus tidak sama dengan 0. Determinan matriks 3×3 dapat dihitung dengan menggunakan rumus:
$$
det(A) = a_{11}(a_{22}a_{33}-a_{23}a_{32}) – a_{12}(a_{21}a_{33}-a_{23}a_{31}) + a_{13}(a_{21}a_{32}-a_{22}a_{31})
$$
Kedua, matriks adjoint dari matriks 3×3 harus dihitung. Adjoints matriks 3×3 dapat dihitung dengan cara mengubah setiap elemen matriks menjadi ko-faktor, kemudian dipindahkan ke posisi yang sesuai.
Langkah-langkah Mencari Invers Matriks 3×3
Setelah memenuhi persyaratan di atas, berikut adalah langkah-langkah untuk mencari invers matriks 3×3.
Langkah 1: Hitung Determinan
Langkah pertama adalah menghitung determinan matriks 3×3. Rumus determinan sudah dijelaskan di atas. Misalnya kita memiliki matriks A:
$$
A = begin{bmatrix}
2 & 3 & 1 \
4 & 1 & 2 \
3 & 4 & 3
end{bmatrix}
$$
Maka determinan matriks A dapat dihitung dengan menggunakan rumus:
$$
det(A) = 2(1 times 3 – 2 times 4) – 3(4 times 3 – 2 times 3) + 1(4 times 4 – 1 times 3) = -17
$$
Jadi determinan matriks A adalah -17.
Langkah 2: Hitung Adjoints
Setelah menghitung determinan, langkah selanjutnya adalah menghitung adjoints matriks. Untuk menghitung adjoints, pertama-tama kita perlu menghitung ko-faktor dari setiap elemen matriks. Ko-faktor dapat dihitung dengan cara mengikuti pola:
$$
C_{ij} = (-1)^{i+j} begin{vmatrix}
a_{kl}
end{vmatrix}
$$
di mana $a_{kl}$ adalah matriks minor dari elemen yang bersangkutan. Matriks minor dapat dihitung dengan cara menghilangkan baris dan kolom yang berkaitan dengan elemen tersebut, kemudian menghitung determinan dari matriks hasil penghilangan tersebut.
Berikut adalah contoh perhitungan adjoints matriks A:
$$
A = begin{bmatrix}
2 & 3 & 1 \
4 & 1 & 2 \
3 & 4 & 3
end{bmatrix}
$$
Kita mulai dengan menghitung matriks minor untuk setiap elemen matriks A. Misalnya, untuk elemen $a_{11}$:
$$
begin{vmatrix}
1 & 2 \
4 & 3
end{vmatrix}
= (1 times 3) – (2 times 4) = -5
$$
Kita lalu mengalikan hasil ini dengan $(-1)^{1+1} = 1$, sehingga ko-faktor untuk $a_{11}$ adalah -5.
Kita melakukan hal yang sama untuk setiap elemen matriks A, sehingga ko-faktor matriks A menjadi:
$$
C = begin{bmatrix}
-5 & 11 & -7 \
-10 & -3 & 8 \
13 & -7 & -2
end{bmatrix}
$$
Kita lalu perlu mentranspos matriks ko-faktor ini, sehingga elemen $C_{ij}$ akan berada di posisi $C_{ji}$. Matriks hasil transpos inilah yang disebut dengan matriks adjoints. Sehingga adjoints dari matriks A adalah:
$$
adj(A) = begin{bmatrix}
-5 & -10 & 13 \
11 & -3 & -7 \
-7 & 8 & -2
end{bmatrix}
$$
Langkah 3: Hitung Invers
Setelah menghitung adjoints, langkah terakhir adalah menghitung invers matriks. Invers matriks dapat dihitung dengan rumus:
$$
A^{-1} = frac{1}{det(A)}adj(A)
$$
Misalnya, untuk matriks A di atas, invers matriksnya dapat dihitung dengan rumus:
$$
A^{-1} = frac{1}{-17}begin{bmatrix}
-5 & -10 & 13 \
11 & -3 & -7 \
-7 & 8 & -2
end{bmatrix} = begin{bmatrix}
frac{5}{17} & frac{10}{17} & -frac{13}{17} \
-frac{11}{17} & frac{3}{17} & frac{7}{17} \
frac{7}{17} & -frac{8}{17} & frac{2}{17}
end{bmatrix}
$$
Sehingga invers matriks A adalah:
$$
A^{-1} = begin{bmatrix}
frac{5}{17} & frac{10}{17} & -frac{13}{17} \
-frac{11}{17} & frac{3}{17} & frac{7}{17} \
frac{7}{17} & -frac{8}{17} & frac{2}{17}
end{bmatrix}
$$
Kesimpulan
Invers matriks 3×3 adalah matriks yang sangat berguna dalam banyak aplikasi matematika. Untuk mencari invers matriks 3×3, ada beberapa persyaratan yang perlu dipenuhi, seperti determinan matriks tidak boleh sama dengan 0. Langkah-langkah untuk mencari invers matriks 3×3 adalah menghitung determinan matriks, menghitung adjoints matriks, dan menghitung invers matriks menggunakan rumus yang sudah disebutkan di atas. Dengan memahami cara mencari invers matriks 3×3, kita dapat memanfaatkannya dalam berbagai aplikasi matematika yang lebih kompleks.
 Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
