Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Daftar Isi
Bentuk Persamaan Kuadrat
Persamaan kuadrat merupakan persamaan dengan bentuk umum ax2 + bx + c = 0, dimana a, b, dan c adalah konstanta. Persamaan ini sering muncul dalam berbagai macam konteks matematika, seperti dalam penyelesaian masalah fisika, ekonomi, dan teknik.
Dalam pembahasan kali ini, kita akan membahas tentang bentuk persamaan kuadrat, yaitu bentuk yang paling umum dan sering ditemui pada soal-soal matematika. Kita akan membahas tentang pengertian, ciri-ciri, serta contoh-contoh soal untuk memudahkan pemahaman.
Pengertian Persamaan Kuadrat
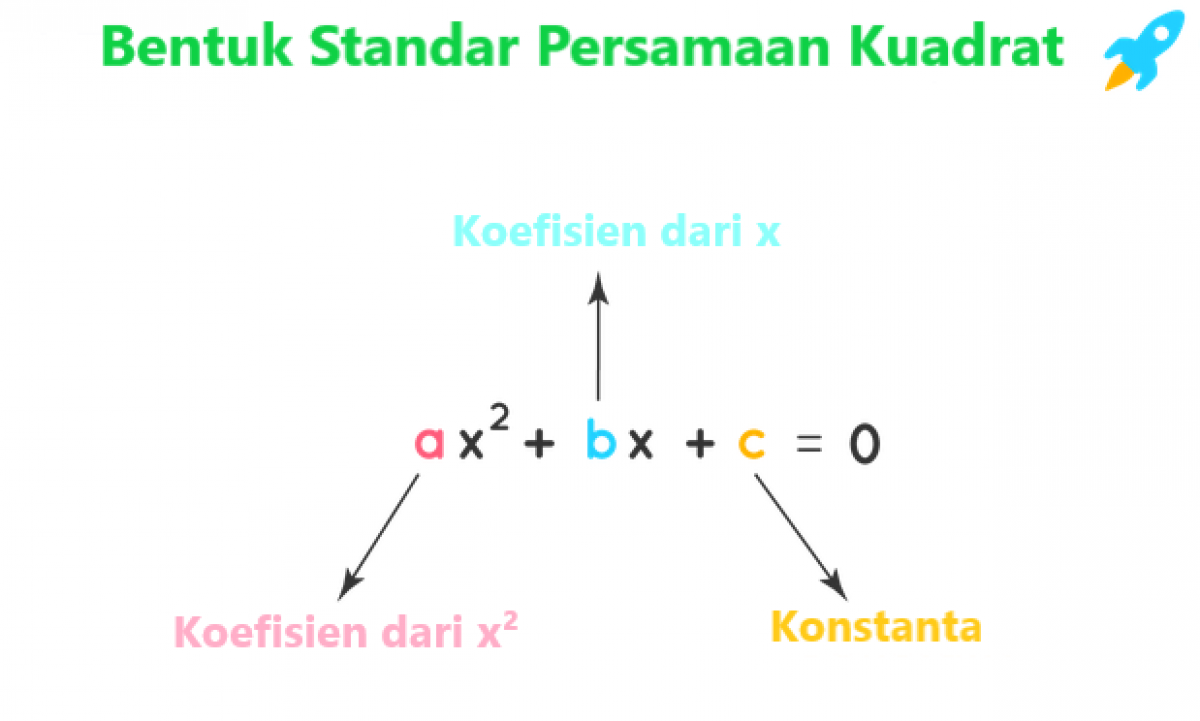
Persamaan kuadrat adalah persamaan yang mengandung suku-suku pangkat dua dengan variabel yang sama. Bentuk umum dari persamaan kuadrat adalah ax2 + bx + c = 0, dimana a, b, dan c adalah konstanta. Persamaan ini biasanya diselesaikan untuk mencari nilai dari variabel x.
Ciri-Ciri Persamaan Kuadrat
Terdapat beberapa ciri-ciri persamaan kuadrat yang perlu diketahui, yaitu:
1. Memiliki variabel pangkat dua
Persamaan kuadrat selalu mengandung suku pangkat dua dengan variabel yang sama. Pada bentuk umum persamaan kuadrat, variabel yang digunakan adalah x.
2. Memiliki dua solusi
Persamaan kuadrat selalu memiliki dua solusi atau akar. Artinya, terdapat dua nilai dari variabel x yang memenuhi persamaan tersebut.
3. Grafiknya berupa parabola
Grafik persamaan kuadrat selalu berupa parabola. Parabola ini dapat membantu kita memahami sifat-sifat dari persamaan kuadrat, seperti titik puncak, arah membuka, dan persilangan dengan sumbu-x dan sumbu-y.
Cara Menyelesaikan Persamaan Kuadrat
Untuk menyelesaikan persamaan kuadrat, terdapat beberapa metode yang dapat digunakan, yaitu:
1. Faktorisasi
Metode faktorisasi digunakan jika persamaan kuadrat dapat difaktorkan. Caranya adalah dengan mencari dua bilangan yang jika dikalikan menghasilkan nilai c dan jika dijumlahkan menghasilkan nilai b. Setelah itu, persamaan kuadrat difaktorkan dengan menggunakan bilangan-bilangan tersebut.
Contoh:
x2 + 5x + 6 = 0
Cari dua bilangan yang jika dikalikan menghasilkan 6 dan jika dijumlahkan menghasilkan 5.
Dua bilangan tersebut adalah 2 dan 3.
Maka persamaan kuadrat dapat difaktorkan menjadi:
(x + 2)(x + 3) = 0
Sehingga nilai x dapat dicari dengan mengatur setiap faktor menjadi nol:
x + 2 = 0 atau x + 3 = 0
x = -2 atau x = -3
2. Rumus kuadrat
Metode rumus kuadrat digunakan jika persamaan kuadrat tidak dapat difaktorisasi. Caranya adalah dengan menggunakan rumus:
x = (-b ± √(b2 – 4ac)) / 2a
Rumus ini digunakan untuk menghitung nilai x pada persamaan kuadrat ax2 + bx + c = 0.
Contoh:
2×2 – 5x + 2 = 0
Maka a = 2, b = -5, dan c = 2.
Substitusikan nilai a, b, dan c ke dalam rumus kuadrat:
x = (-(-5) ± √((-5)2 – 4(2)(2))) / 2(2)
x = (5 ± √17) / 4
Sehingga nilai x dapat dicari dengan menggunakan dua solusi:
x1 = (5 + √17) / 4
x2 = (5 – √17) / 4
3. Metode grafik
Metode grafik digunakan untuk menggambar grafik persamaan kuadrat dan menentukan nilai-nilai x yang memenuhi persamaan tersebut.
Caranya adalah dengan mengubah persamaan kuadrat menjadi bentuk akar-akar:
(x – x1)(x – x2) = 0
Dimana x1 dan x2 adalah akar-akar dari persamaan kuadrat.
Setelah itu, gambarlah grafik persamaan kuadrat tersebut dengan menggunakan titik-titik x1 dan x2 sebagai titik-titik yang dilewati oleh grafik. Setelah itu, tentukanlah nilai-nilai x yang memenuhi persamaan dengan melihat persilangan grafik dengan sumbu-x.
Contoh Soal Persamaan Kuadrat
1. Selesaikan persamaan kuadrat berikut dengan faktorisasi:
x2 – 4x – 5 = 0
Jawab:
Cari dua bilangan yang jika dikalikan menghasilkan -5 dan jika dijumlahkan menghasilkan -4.
Dua bilangan tersebut adalah -5 dan 1.
Maka persamaan kuadrat dapat difaktorkan menjadi:
(x – 5)(x + 1) = 0
Sehingga nilai x dapat dicari dengan mengatur setiap faktor menjadi nol:
x – 5 = 0 atau x + 1 = 0
x = 5 atau x = -1
2. Selesaikan persamaan kuadrat berikut dengan menggunakan rumus kuadrat:
3×2 + 4x – 1 = 0
Jawab:
Maka a = 3, b = 4, dan c = -1.
Substitusikan nilai a, b, dan c ke dalam rumus kuadrat:
x = (-4 ± √(42 – 4(3)(-1))) / 2(3)
x = (-4 ± √28) / 6
Sehingga nilai x dapat dicari dengan menggunakan dua solusi:
x1 = (-4 + √28) / 6
x2 = (-4 – √28) / 6
3. Gambar grafik persamaan kuadrat berikut dan tentukan nilai-nilai x yang memenuhi persamaan:
y = x2 – 4x + 3
Jawab:
Untuk menggambar grafik persamaan kuadrat tersebut, pertama-tama tentukan titik-titik x1 dan x2 yang memenuhi persamaan. Caranya adalah dengan mencari nilai dari diskriminan persamaan kuadrat:
D = b2 – 4ac
D = (-4)2 – 4(1)(3)
D = 4
Maka akar-akar dari persamaan kuadrat tersebut adalah:
x1 = 1
x2 = 3
Setelah itu, gambarkan grafik persamaan kuadrat dengan menggunakan titik-titik x1 dan x2 sebagai titik-titik yang dilewati oleh grafik. Dari grafik tersebut, dapat dilihat bahwa nilai-nilai x yang memenuhi persamaan adalah antara 1 dan 3.
Kesimpulan
Persamaan kuadrat adalah persamaan yang mengandung suku-suku pangkat dua dengan variabel yang sama. Bentuk umum dari persamaan kuadrat adalah ax2 + bx + c = 0, dimana a, b, dan c adalah konstanta. Persamaan ini dapat diselesaikan dengan menggunakan metode faktorisasi, rumus kuadrat, atau metode grafik. Terdapat beberapa ciri-ciri persamaan kuadrat, yaitu selalu mengandung variabel pangkat dua, memiliki dua solusi, dan grafiknya berupa parabola.
