Rumus Volume Bangun Ruang
Bangun ruang adalah sebuah benda matematika tiga dimensi yang mempunyai bentuk atau wujud tertentu. Volume bangun ruang adalah ukuran besarnya ruang yang dapat diisi oleh sebuah bangun ruang. Untuk menghitung volume bangun ruang, kita perlu menggunakan rumus volume yang sesuai dengan jenis bangun ruang yang diinginkan. Berikut adalah rumus volume bangun ruang dan langkah-langkahnya.
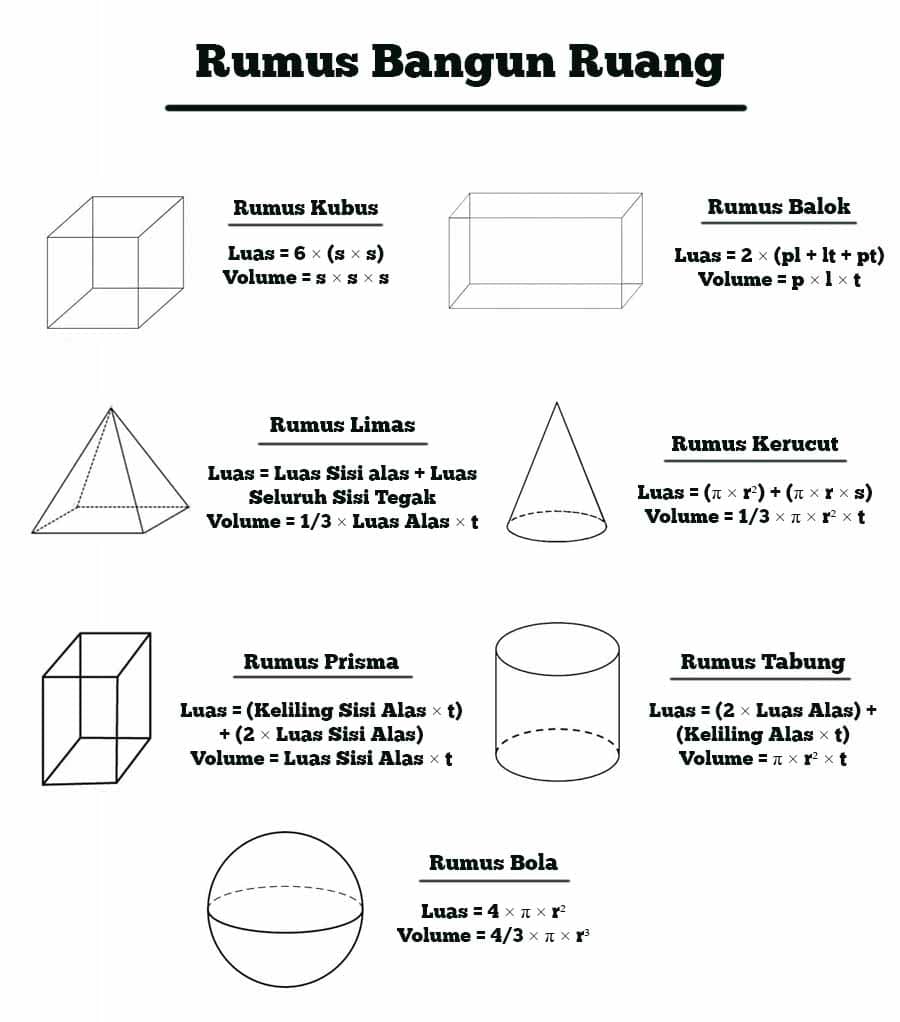
1. Kubus
Kubus adalah sebuah bangun ruang tiga dimensi yang memiliki enam sisi persegi yang sama besar dan terdiri atas 12 rusuk sama panjang. Untuk menghitung volume kubus, kita dapat menggunakan rumus berikut.
Rumus:
V = s x s x s
Keterangan:
V = Volume kubus
s = Sisi kubus
Contoh soal:
Sebuah kubus memiliki panjang sisi 10 cm. Hitunglah volume kubus tersebut.
Penyelesaian:
V = s x s x s
V = 10 cm x 10 cm x 10 cm
V = 1000 cm³
Jadi, volume kubus tersebut adalah 1000 cm³.
2. Balok
Balok adalah sebuah bangun ruang tiga dimensi yang memiliki enam sisi (tiga pasang sisi yang sama besar). Untuk menghitung volume balok, kita dapat menggunakan rumus berikut.
Rumus:
V = p x l x t
Keterangan:
V = Volume balok
p = Panjang balok
l = Lebar balok
t = Tinggi balok
Contoh soal:
Sebuah balok memiliki panjang 12 cm, lebar 8 cm, dan tinggi 5 cm. Hitunglah volume balok tersebut.
Penyelesaian:
V = p x l x t
V = 12 cm x 8 cm x 5 cm
V = 480 cm³
Jadi, volume balok tersebut adalah 480 cm³.
3. Prisma Segitiga
Prisma Segitiga adalah sebuah bangun ruang tiga dimensi yang memiliki dua alas segitiga yang sejajar dan memiliki tiga pasang sisi yang sama besar. Untuk menghitung volume prisma segitiga, kita dapat menggunakan rumus berikut.
Rumus:
V = ½ x a x t x t’
Keterangan:
V = Volume prisma segitiga
a = Luas alas segitiga
t = Tinggi prisma
t’ = Tinggi segitiga
Contoh soal:
Sebuah prisma segitiga memiliki alas segitiga dengan panjang 10 cm dan tinggi 6 cm. Tinggi prisma adalah 8 cm. Hitunglah volume prisma segitiga tersebut.
Penyelesaian:
a = ½ x alas x tinggi segitiga
a = ½ x 10 cm x 6 cm
a = 30 cm²
V = ½ x a x t x t’
V = ½ x 30 cm² x 8 cm x 6 cm
V = 720 cm³
Jadi, volume prisma segitiga tersebut adalah 720 cm³.
4. Limas Segitiga
Limas Segitiga adalah sebuah bangun ruang tiga dimensi yang memiliki alas segitiga dan enam sisi yang sama besar. Untuk menghitung volume limas segitiga, kita dapat menggunakan rumus berikut.
Rumus:
V = ½ x a x t
Keterangan:
V = Volume limas segitiga
a = Luas alas segitiga
t = Tinggi limas
Contoh soal:
Sebuah limas segitiga memiliki alas segitiga dengan panjang 8 cm dan tinggi 6 cm. Tinggi limas adalah 10 cm. Hitunglah volume limas segitiga tersebut.
Penyelesaian:
a = ½ x alas x tinggi segitiga
a = ½ x 8 cm x 6 cm
a = 24 cm²
V = ½ x a x t
V = ½ x 24 cm² x 10 cm
V = 120 cm³
Jadi, volume limas segitiga tersebut adalah 120 cm³.
5. Tabung
Tabung adalah sebuah bangun ruang tiga dimensi yang memiliki dua lingkaran identik pada kedua ujungnya dan berbentuk silinder. Untuk menghitung volume tabung, kita dapat menggunakan rumus berikut.
Rumus:
V = π x r² x t
Keterangan:
V = Volume tabung
π = Konstanta pi (3.14)
r = Jari-jari tabung
t = Tinggi tabung
Contoh soal:
Sebuah tabung memiliki jari-jari 5 cm dan tinggi 10 cm. Hitunglah volume tabung tersebut.
Penyelesaian:
V = π x r² x t
V = 3.14 x 5 cm x 5 cm x 10 cm
V = 785 cm³
Jadi, volume tabung tersebut adalah 785 cm³.
6. Kerucut
Kerucut adalah sebuah bangun ruang tiga dimensi yang memiliki satu lingkaran pada alasnya dan ujungnya berbentuk tumpul. Untuk menghitung volume kerucut, kita dapat menggunakan rumus berikut.
Rumus:
V = 1/3 x π x r² x t
Keterangan:
V = Volume kerucut
π = Konstanta pi (3.14)
r = Jari-jari kerucut
t = Tinggi kerucut
Contoh soal:
Sebuah kerucut memiliki jari-jari 6 cm dan tinggi 10 cm. Hitunglah volume kerucut tersebut.
Penyelesaian:
V = 1/3 x π x r² x t
V = 1/3 x 3.14 x 6 cm x 6 cm x 10 cm
V = 376.8 cm³
Jadi, volume kerucut tersebut adalah 376.8 cm³.
7. Bola
Bola adalah sebuah bangun ruang tiga dimensi yang tidak memiliki sudut dan semua titiknya sama jauh dari titik pusatnya. Untuk menghitung volume bola, kita dapat menggunakan rumus berikut.
Rumus:
V = 4/3 x π x r³
Keterangan:
V = Volume bola
π = Konstanta pi (3.14)
r = Jari-jari bola
Contoh soal:
Sebuah bola memiliki jari-jari 8 cm. Hitunglah volume bola tersebut.
Penyelesaian:
V = 4/3 x π x r³
V = 4/3 x 3.14 x 8 cm x 8 cm x 8 cm
V = 2144.96 cm³
Jadi, volume bola tersebut adalah 2144.96 cm³.
Kesimpulan
Volume bangun ruang dapat dihitung menggunakan rumus volume yang sesuai dengan jenis bangun ruang yang diinginkan. Rumus volume kubus adalah V = s x s x s, rumus volume balok adalah V = p x l x t, rumus volume prisma segitiga adalah V = ½ x a x t x t’, rumus volume limas segitiga adalah V = ½ x a x t, rumus volume tabung adalah V = π x r² x t, rumus volume kerucut adalah V = 1/3 x π x r² x t, dan rumus volume bola adalah V = 4/3 x π x r³. Dalam menghitung volume bangun ruang, pastikan satuan ukuran yang digunakan sama untuk setiap variabel.
 Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
