Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Daftar Isi
Rumus Rumus Bangun Ruang
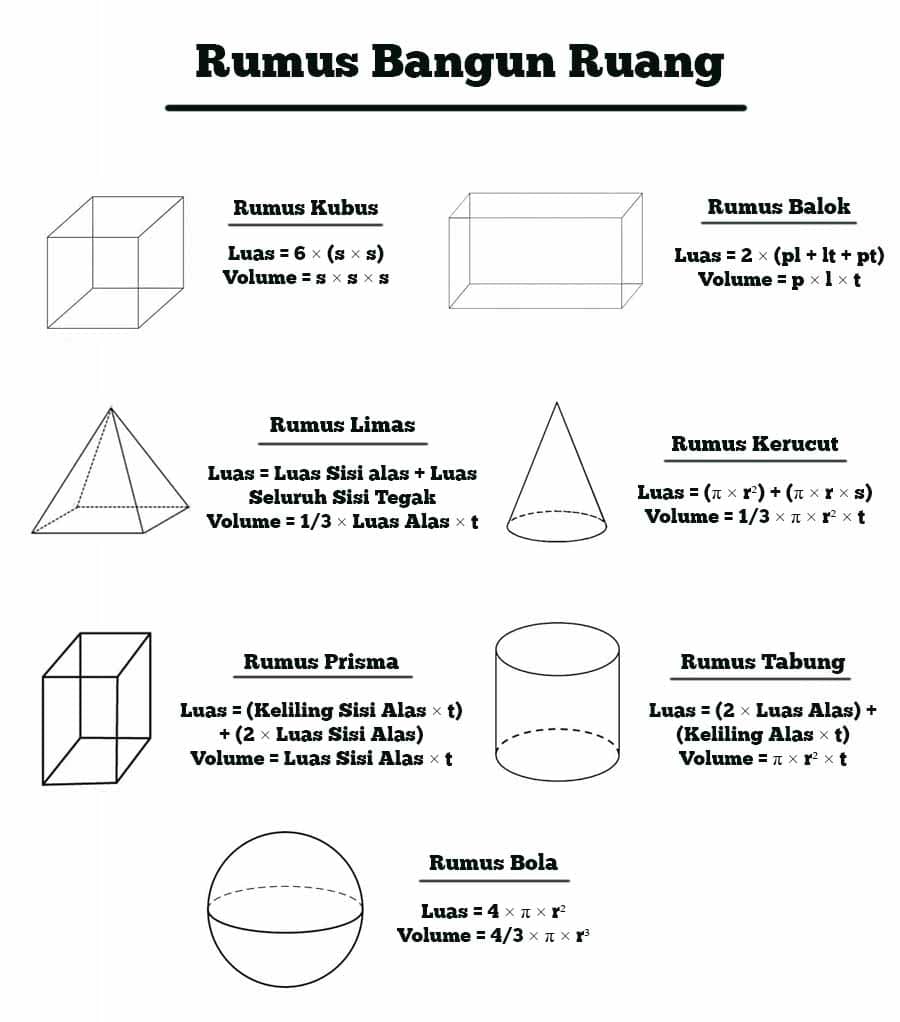
Bangun ruang adalah benda geometri tiga dimensi yang memiliki sisi, rusuk, dan sudut. Kita bisa menemukan bangun ruang di sekitar kita, seperti balok, kubus, prisma, limas, tabung, bola, dan kerucut. Untuk menghitung luas dan volume bangun ruang, kita harus menggunakan rumus-rumus yang tepat. Berikut ini adalah rumus-rumus bangun ruang yang sering digunakan.
Rumus Bangun Ruang Dua Dimensi
1. Persegi
Persegi adalah bangun ruang yang memiliki empat sisi yang sama panjang dan empat sudut yang sama besar. Luas persegi dapat dihitung dengan rumus:
Luas = sisi x sisi
Contoh: Jika sisi persegi adalah 5 cm, maka luasnya adalah 25 cm².
2. Persegi panjang
Persegi panjang adalah bangun ruang yang memiliki empat sisi, dua sisi yang sama panjang dan dua sisi yang sama panjang. Luas persegi panjang dapat dihitung dengan rumus:
Luas = panjang x lebar
Contoh: Jika panjang persegi panjang adalah 6 cm dan lebarnya adalah 4 cm, maka luasnya adalah 24 cm².
3. Segitiga
Segitiga adalah bangun ruang yang memiliki tiga sisi dan tiga sudut. Luas segitiga dapat dihitung dengan rumus:
Luas = 1/2 x alas x tinggi
Contoh: Jika alas segitiga adalah 8 cm dan tingginya adalah 6 cm, maka luasnya adalah 24 cm².
4. Lingkaran
Lingkaran adalah bangun ruang yang memiliki jari-jari yang sama panjang dari setiap titik pada lingkaran ke pusatnya. Luas lingkaran dapat dihitung dengan rumus:
Luas = π x r²
Contoh: Jika jari-jari lingkaran adalah 5 cm, maka luasnya adalah 78.5 cm².
Rumus Bangun Ruang Tiga Dimensi
1. Balok
Balok adalah bangun ruang yang memiliki enam sisi, yang terdiri dari empat sisi persegi dan dua sisi persegi panjang. Luas permukaan balok dapat dihitung dengan rumus:
Luas permukaan = 2 x (panjang x lebar + panjang x tinggi + lebar x tinggi)
Contoh: Jika panjang balok adalah 6 cm, lebar 4 cm, dan tinggi 5 cm, maka luas permukaannya adalah 116 cm².
2. Kubus
Kubus adalah bangun ruang yang memiliki enam sisi yang sama panjang. Luas permukaan kubus dapat dihitung dengan rumus:
Luas permukaan = 6 x sisi²
Contoh: Jika sisi kubus adalah 4 cm, maka luas permukaannya adalah 96 cm².
3. Prisma
Prisma adalah bangun ruang yang memiliki dua sisi segitiga atau persegi sebagai alas dan sisi-sisi serupa. Luas permukaan prisma dapat dihitung dengan rumus:
Luas permukaan = 2 x luas alas + keliling alas x tinggi
Contoh: Jika alas prisma adalah persegi dengan panjang sisi 4 cm dan tingginya 5 cm serta tinggi prisma 8 cm, maka luas permukaannya adalah 112 cm².
4. Limas
Limas adalah bangun ruang yang memiliki satu sisi alas segitiga atau persegi dan satu sisi atas yang sama dengan alas. Luas permukaan limas dapat dihitung dengan rumus:
Luas permukaan = luas alas + luas selubung limas
Luas selubung limas dapat dihitung dengan rumus:
Luas selubung = 1/2 x keliling alas x slant height
Contoh: Jika alas limas adalah segitiga dengan alas 6 cm, tinggi 8 cm, dan tinggi limas 10 cm, maka luas permukaannya adalah 148 cm².
5. Tabung
Tabung adalah bangun ruang yang memiliki dua lingkaran dan sisi-sisi berbentuk persegi panjang. Luas permukaan tabung dapat dihitung dengan rumus:
Luas permukaan = 2 x luas lingkaran + keliling lingkaran x tinggi
Contoh: Jika jari-jari tabung adalah 4 cm dan tingginya 10 cm, maka luas permukaannya adalah 226.2 cm².
6. Bola
Bola adalah bangun ruang yang memiliki semua titik pada permukaannya sama jauh dari pusatnya. Luas permukaan bola dapat dihitung dengan rumus:
Luas permukaan = 4 x π x r²
Contoh: Jika jari-jari bola adalah 5 cm, maka luas permukaannya adalah 314.2 cm².
7. Kerucut
Kerucut adalah bangun ruang yang memiliki alas lingkaran dan satu sisi melengkung ke atas. Luas permukaan kerucut dapat dihitung dengan rumus:
Luas permukaan = luas alas + luas selimut kerucut
Luas selimut kerucut dapat dihitung dengan rumus:
Luas selimut = π x r x slant height
Contoh: Jika jari-jari kerucut adalah 6 cm dan tingginya 8 cm, maka luas permukaannya adalah 150.8 cm².
Kesimpulan
Menghitung luas dan volume bangun ruang adalah hal yang penting dalam matematika. Dengan menggunakan rumus-rumus yang tepat, kita dapat menghitung dengan mudah dan akurat. Rumus-rumus bangun ruang yang telah dijelaskan di atas dapat digunakan sebagai referensi dalam menghitung luas dan volume bangun ruang.
