Rumus Rumus Balok dan Cara Menghitungnya

Balok adalah salah satu bentuk bangun ruang yang sering kita temukan dalam kehidupan sehari-hari. Balok memiliki enam sisi, yaitu dua sisi persegi panjang di bagian atas dan bawah, serta empat sisi persegi panjang lainnya yang menyambungkan keduanya. Untuk menghitung berbagai macam parameter balok, seperti luas permukaan, volume, dan diagonal, kita memerlukan rumus-rumus balok. Berikut ini akan dijelaskan rumus-rumus balok beserta cara menghitungnya.

Rumus Volume Balok

Volume balok adalah ukuran dari ruang yang dapat diisi oleh balok tersebut. Volume balok dapat dihitung dengan rumus:

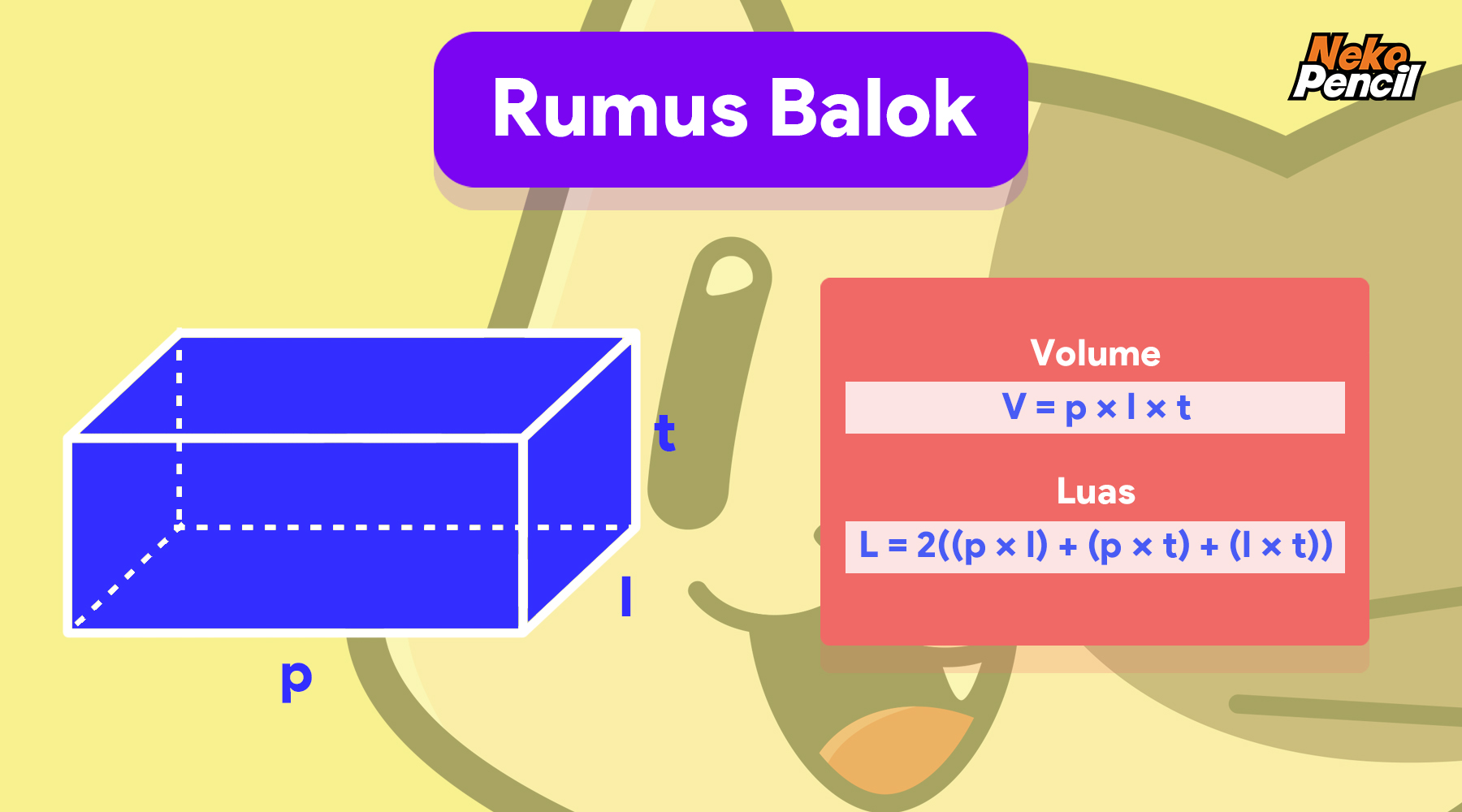
V = p x l x t

Keterangan:
– V = volume balok
– p = panjang balok
– l = lebar balok
– t = tinggi balok

Contoh soal:
Sebuah balok memiliki panjang 5 cm, lebar 3 cm, dan tinggi 2 cm. Berapa volume balok tersebut?

Penyelesaian:
V = p x l x t
V = 5 cm x 3 cm x 2 cm
V = 30 cm³

Jadi, volume balok tersebut adalah 30 cm³.

Rumus Luas Permukaan Balok

Luas permukaan balok adalah ukuran dari seluruh luas permukaan balok, yaitu jumlah luas sisi-sisi balok. Luas permukaan balok dapat dihitung dengan rumus:

L = 2(pl + pt + lt)

Keterangan:
– L = luas permukaan balok
– p = panjang balok
– l = lebar balok
– t = tinggi balok

Contoh soal:
Sebuah balok memiliki panjang 5 cm, lebar 3 cm, dan tinggi 2 cm. Berapa luas permukaan balok tersebut?

Penyelesaian:
L = 2(pl + pt + lt)
L = 2((5 cm x 3 cm) + (5 cm x 2 cm) + (3 cm x 2 cm))
L = 2(15 cm² + 10 cm² + 6 cm²)
L = 2 x 31 cm²
L = 62 cm²

Jadi, luas permukaan balok tersebut adalah 62 cm².

Rumus Diagonal Balok

Diagonal balok adalah garis lurus yang menghubungkan dua titik sudut yang berlawanan pada balok. Diagonal balok dapat dihitung dengan rumus:

d = √(p² + l² + t²)

Keterangan:
– d = diagonal balok
– p = panjang balok
– l = lebar balok
– t = tinggi balok

Contoh soal:
Sebuah balok memiliki panjang 5 cm, lebar 3 cm, dan tinggi 2 cm. Berapa panjang diagonal balok tersebut?

Penyelesaian:
d = √(p² + l² + t²)
d = √(5 cm² + 3 cm² + 2 cm²)
d = √34 cm
d ≈ 5,83 cm

Jadi, panjang diagonal balok tersebut adalah sekitar 5,83 cm.

Rumus Berat Jenis Balok

Berat jenis balok adalah besarnya massa balok per satuan volume. Berat jenis balok dapat dihitung dengan rumus:

ρ = m/V

Keterangan:
– ρ = berat jenis balok
– m = massa balok
– V = volume balok

Contoh soal:
Sebuah balok memiliki massa 4 kg dan volume 30 cm³. Berapa berat jenis balok tersebut?

Penyelesaian:
ρ = m/V
ρ = 4 kg/0,03 m³
ρ ≈ 133,33 kg/m³

Jadi, berat jenis balok tersebut adalah sekitar 133,33 kg/m³.

Rumus Massa Jenis Balok

Massa jenis balok adalah besarnya massa balok per satuan volume. Massa jenis balok dapat dihitung dengan rumus:

ρ = m/V

Keterangan:
– ρ = massa jenis balok
– m = massa balok
– V = volume balok

Contoh soal:
Sebuah balok memiliki massa 4 kg dan volume 30 cm³. Berapa massa jenis balok tersebut?

Penyelesaian:
ρ = m/V
ρ = 4 kg/0,03 m³
ρ ≈ 133,33 kg/m³

Jadi, massa jenis balok tersebut adalah sekitar 133,33 kg/m³.

Rumus Daya Dukung Balok

Daya dukung balok adalah besarnya beban maksimum yang dapat diangkat oleh balok tanpa menyebabkan kerusakan pada balok tersebut. Daya dukung balok dapat dihitung dengan rumus:

FD = (σ x I)/y

Keterangan:
– FD = daya dukung balok
– σ = tegangan maksimum pada balok
– I = momen inersia balok
– y = jarak titik netral balok dari sisi atas balok

Contoh soal:
Sebuah balok memiliki panjang 5 m, lebar 10 cm, dan tinggi 20 cm. Balok tersebut diletakkan dengan lebar pada atas dan tinggi pada samping. Jika tegangan maksimum pada balok adalah 20 N/m², momen inersia balok adalah 4000 cm⁴, dan jarak titik netral balok dari sisi atas balok adalah 10 cm, berapa daya dukung balok tersebut?

Penyelesaian:
FD = (σ x I)/y
FD = (20 N/m² x 4000 cm⁴)/10 cm
FD = 800000 Ncm
FD = 8000 Nm

Jadi, daya dukung balok tersebut adalah 8000 Nm.

Kesimpulan

Dari penjelasan di atas, dapat disimpulkan bahwa rumus-rumus balok sangatlah penting untuk menghitung berbagai macam parameter balok, seperti volume, luas permukaan, diagonal, berat jenis, massa jenis, dan daya dukung. Dengan memahami rumus-rumus balok dan cara menghitungnya, kita dapat meningkatkan kemampuan kita dalam memecahkan masalah yang berkaitan dengan balok. Oleh karena itu, penting bagi kita untuk mempelajari dan memahami rumus-rumus balok.