Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Daftar Isi
Pengenalan Rumus Pertidaksamaan
Rumus Pertidaksamaan adalah rumus matematika yang digunakan untuk menyelesaikan persamaan yang tidak sama atau tidak setara. Persamaan tersebut terdiri dari dua ekspresi matematika yang dihubungkan oleh tanda pertidaksamaan. Contohnya, 2x + 3 > 5x – 1. Dalam hal ini, ekspresi pada sisi kiri tanda pertidaksamaan lebih besar dari ekspresi pada sisi kanan tanda pertidaksamaan.
Rumus Pertidaksamaan sangat penting dalam matematika karena digunakan dalam berbagai situasi. Misalnya, ketika menyelesaikan masalah matematika, menentukan rentang nilai yang memenuhi persamaan dan ketika menyelesaikan masalah ekonomi dan keuangan.
Jenis Pertidaksamaan
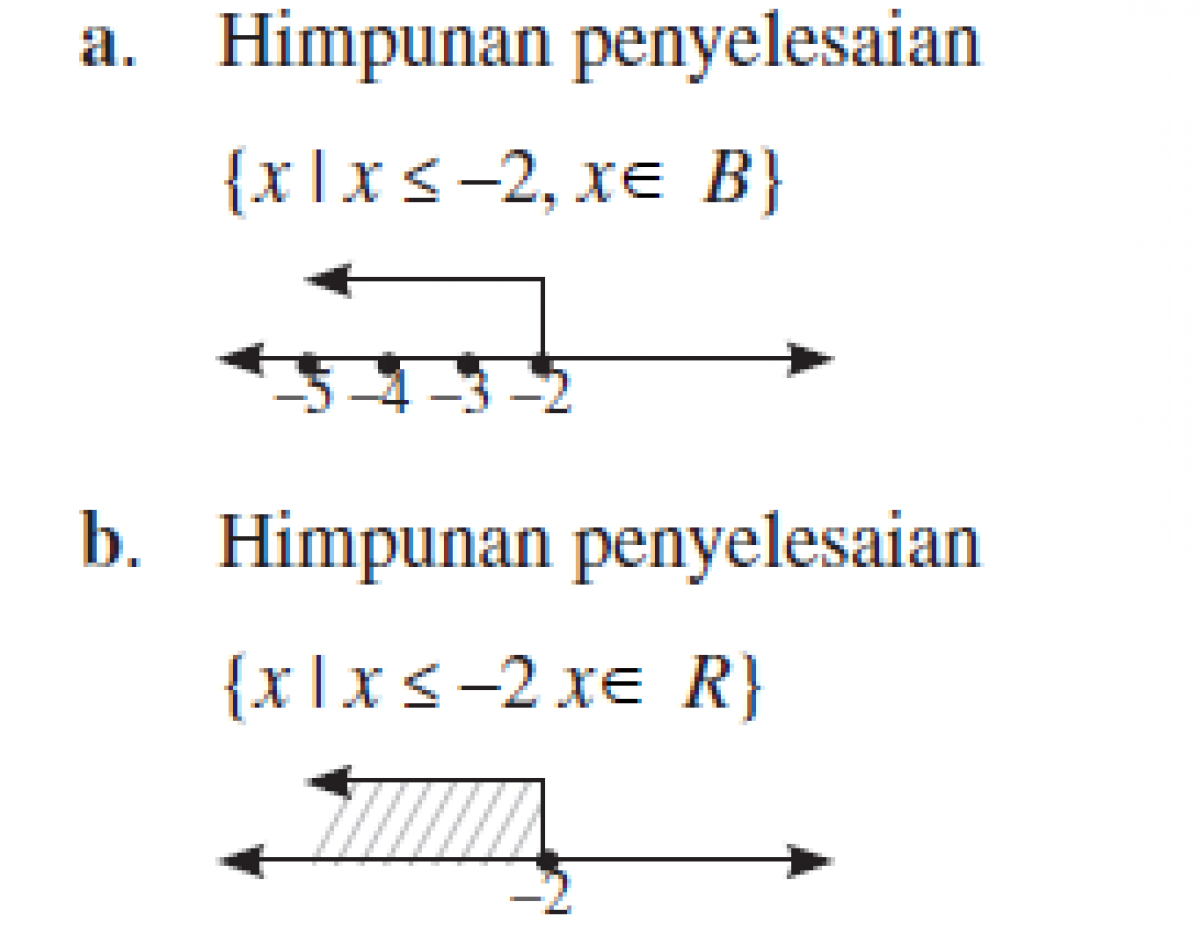
Secara umum, terdapat tiga jenis pertidaksamaan yaitu:
1. Pertidaksamaan Linear
Pertidaksamaan linear adalah pertidaksamaan yang mempunyai bentuk seperti ax + b > c atau ax + b < c. Pertidaksamaan linear dapat diselesaikan dengan memindahkan variabel ke satu sisi dan konstanta ke sisi lainnya. 2. Pertidaksamaan Kuadrat Pertidaksamaan kuadrat adalah pertidaksamaan yang mempunyai bentuk seperti ax² + bx + c > 0 atau ax² + bx + c < 0. Pertidaksamaan ini dapat diselesaikan dengan menggunakan faktorisasi, penggunaan rumus kuadrat, atau dengan menggunakan metode grafik. 3. Pertidaksamaan Rasional Pertidaksamaan rasional adalah pertidaksamaan yang mempunyai bentuk seperti (ax + b)/(cx + d) > 0 atau (ax + b)/(cx + d) < 0. Pertidaksamaan rasional ini dapat diselesaikan dengan menggunakan metode faktorisasi dan mencari akar-akar persamaan.
Cara Menyelesaikan Pertidaksamaan Linear
Berikut ini adalah langkah-langkah untuk menyelesaikan pertidaksamaan linear:
1. Langkah pertama adalah menyederhanakan persamaan jika mungkin. Misalnya, jika persamaan adalah 8x + 4 > 12x – 6, maka persamaan dapat disederhanakan menjadi 4x + 4 > -6x.
2. Langkah kedua adalah memindahkan variabel ke satu sisi dan konstanta ke sisi lainnya. Misalnya, jika persamaan adalah 4x + 4 > -6x, maka kita dapat memindahkan 4x ke sisi kanan dan -4 ke sisi kiri. Sehingga, persamaan menjadi 8x > -8.
3. Langkah ketiga adalah membagi kedua sisi dengan bilangan yang sama untuk mendapatkan nilai variabel. Misalnya, jika persamaan adalah 8x > -8, maka kita dapat membagi kedua sisi dengan 8. Sehingga, persamaan menjadi x > -1.
4. Langkah keempat adalah mengecek apakah nilai yang diperoleh benar atau tidak. Misalnya, jika kita ingin mengecek apakah nilai x > -1 benar atau tidak, kita dapat memasukkan nilai x = -2 ke dalam persamaan. Jika persamaan tersebut benar, maka nilai x > -1 juga benar.
Cara Menyelesaikan Pertidaksamaan Kuadrat
Berikut ini adalah langkah-langkah untuk menyelesaikan pertidaksamaan kuadrat:
1. Langkah pertama adalah menyederhanakan persamaan jika mungkin. Misalnya, jika persamaan adalah 2x² + 3x – 5 < 0, maka persamaan tidak dapat disederhanakan lagi. 2. Langkah kedua adalah mencari akar-akar persamaan. Akar persamaan dapat dicari dengan menggunakan faktorisasi, rumus kuadrat, atau dengan menggunakan metode grafik. 3. Langkah ketiga adalah menentukan tanda nilai variabel pada setiap rentang nilai. Untuk melakukan hal ini, kita dapat menggunakan tabel tanda atau diagram garis bilangan. 4. Langkah keempat adalah mengecek apakah nilai yang diperoleh benar atau tidak. Misalnya, jika kita ingin mengecek apakah nilai x = 2 memenuhi persamaan 2x² + 3x – 5 < 0 atau tidak, kita dapat memasukkan nilai tersebut ke dalam persamaan. Jika persamaan tersebut benar, maka nilai x = 2 memenuhi persamaan.
Cara Menyelesaikan Pertidaksamaan Rasional
Berikut ini adalah langkah-langkah untuk menyelesaikan pertidaksamaan rasional:
1. Langkah pertama adalah menyederhanakan persamaan jika mungkin. Misalnya, jika persamaan adalah (3x + 4)/(2x – 1) > 0, maka persamaan tidak dapat disederhanakan lagi.
2. Langkah kedua adalah mencari akar-akar persamaan. Akar persamaan dapat dicari dengan menggunakan faktorisasi dan mencari akar-akar persamaan.
3. Langkah ketiga adalah menentukan tanda nilai variabel pada setiap rentang nilai. Untuk melakukan hal ini, kita dapat menggunakan tabel tanda atau diagram garis bilangan.
4. Langkah keempat adalah mengecek apakah nilai yang diperoleh benar atau tidak. Misalnya, jika kita ingin mengecek apakah nilai x = 1 memenuhi persamaan (3x + 4)/(2x – 1) > 0 atau tidak, kita dapat memasukkan nilai tersebut ke dalam persamaan. Jika persamaan tersebut benar, maka nilai x = 1 memenuhi persamaan.
Kesimpulan
Rumus Pertidaksamaan adalah rumus matematika yang digunakan untuk menyelesaikan persamaan yang tidak sama atau tidak setara. Terdapat tiga jenis pertidaksamaan yaitu pertidaksamaan linear, pertidaksamaan kuadrat, dan pertidaksamaan rasional. Setiap jenis pertidaksamaan memiliki langkah-langkah yang berbeda untuk menyelesaikannya. Dalam menyelesaikan pertidaksamaan, langkah-langkah yang tepat harus diikuti untuk mendapatkan hasil yang benar.
