Daftar Isi
Rumus Perpangkatan Dan Bentuk Akar
Perpangkatan adalah operasi matematika yang digunakan untuk mengalikan suatu bilangan dengan dirinya sendiri sebanyak n kali. Sedangkan bentuk akar adalah operasi yang digunakan untuk menentukan akar dari suatu bilangan. Kedua operasi tersebut merupakan bagian penting dalam matematika, terutama dalam pemecahan masalah yang melibatkan perhitungan kuadrat atau pangkat tertentu. Dalam artikel ini, akan dibahas tentang rumus perpangkatan dan bentuk akar beserta contoh soal dan cara penyelesaiannya.
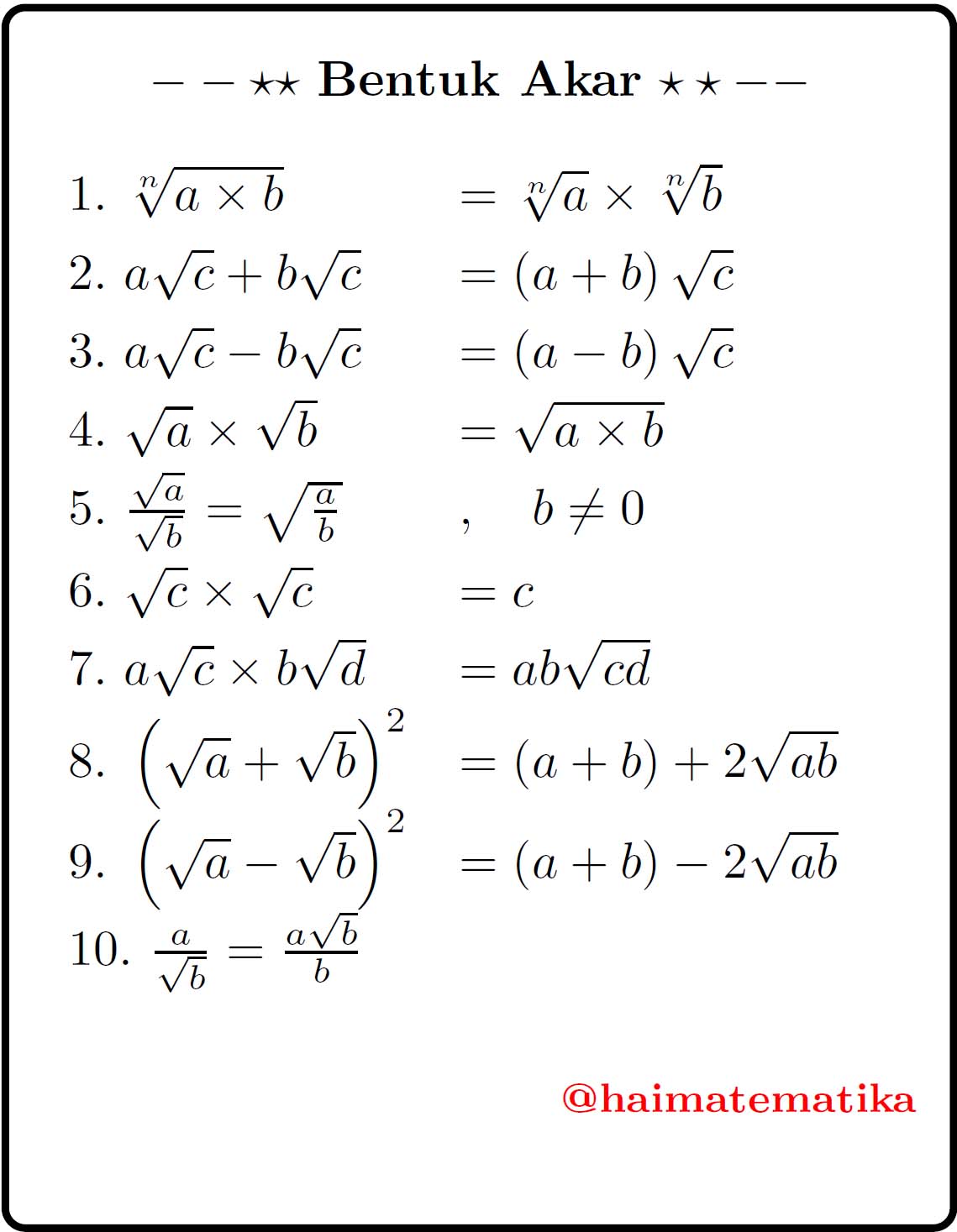
Rumus Perpangkatan
Rumus perpangkatan umumnya digunakan dalam perhitungan matematika, fisika, dan ilmu lainnya. Dalam perpangkatan, bilangan yang ingin dipangkatkan disebut sebagai basis dan pangkatnya disebut sebagai eksponen. Basis dan eksponen ditulis dengan format sebagai berikut: Basis^Eksponen.
Contoh: 2^3
Pada contoh di atas, bilangan 2 merupakan basis dan 3 adalah eksponen. Artinya, bilangan 2 akan dikalikan dengan dirinya sendiri sebanyak 3 kali.
Berikut adalah rumus perpangkatan beserta contoh soal dan cara penyelesaiannya.
Rumus Perpangkatan
Basis^Eksponen = Hasil
Contoh Soal dan Cara Penyelesaiannya
Contoh Soal 1: Hitunglah 3^4
Cara Penyelesaian:
3^4 = 3 x 3 x 3 x 3
= 81
Jadi, 3^4 = 81
Contoh Soal 2: Hitunglah 5^3
Cara Penyelesaian:
5^3 = 5 x 5 x 5
= 125
Jadi, 5^3 = 125
Contoh Soal 3: Hitunglah 2^5
Cara Penyelesaian:
2^5 = 2 x 2 x 2 x 2 x 2
= 32
Jadi, 2^5 = 32
Selain rumus perpangkatan, terdapat beberapa jenis perpangkatan yang sering digunakan dalam matematika. Berikut adalah jenis-jenis perpangkatan tersebut:
1. Perpangkatan bilangan bulat positif
Perpangkatan bilangan bulat positif adalah perpangkatan yang hasilnya selalu positif. Misalnya, 2^3 = 2 x 2 x 2 = 8. Hasil dari perpangkatan bilangan bulat positif selalu berupa bilangan positif.
2. Perpangkatan bilangan bulat negatif
Perpangkatan bilangan bulat negatif adalah perpangkatan yang hasilnya selalu negatif. Misalnya, (-2)^3 = (-2) x (-2) x (-2) = -8. Hasil dari perpangkatan bilangan bulat negatif selalu berupa bilangan negatif.
3. Perpangkatan bilangan pecahan
Perpangkatan bilangan pecahan adalah perpangkatan yang basisnya berupa bilangan pecahan. Misalnya, (1/2)^3 = (1/2) x (1/2) x (1/2) = 1/8. Hasil dari perpangkatan bilangan pecahan selalu berupa bilangan pecahan.
4. Perpangkatan bilangan nol
Perpangkatan bilangan nol adalah perpangkatan yang basisnya adalah nol. Misalnya, 0^3 = 0 x 0 x 0 = 0. Hasil dari perpangkatan bilangan nol selalu berupa nol.
5. Perpangkatan bilangan satu
Perpangkatan bilangan satu adalah perpangkatan yang basisnya adalah satu. Misalnya, 1^3 = 1 x 1 x 1 = 1. Hasil dari perpangkatan bilangan satu selalu berupa satu.
Rumus Bentuk Akar
Bentuk akar adalah kebalikan dari perpangkatan. Bentuk akar digunakan untuk menentukan bilangan yang hasil perpangkatannya sama dengan bilangan yang diakarkan. Bentuk akar ditulis dengan menggunakan simbol akar dan bilangan yang diakarkan di dalamnya.
Contoh: √25
Pada contoh di atas, bilangan 25 diakarkan dan ditulis dalam simbol akar. Artinya, bilangan yang jika dipangkatkan dua kali akan menghasilkan 25.
Berikut adalah rumus bentuk akar beserta contoh soal dan cara penyelesaiannya.
Rumus Bentuk Akar
√Bilangan = Hasil
Contoh Soal dan Cara Penyelesaiannya
Contoh Soal 1: Tentukanlah akar dari 49
Cara Penyelesaian:
√49 = √(7 x 7) = 7
Jadi, akar dari 49 adalah 7.
Contoh Soal 2: Tentukanlah akar dari 36
Cara Penyelesaian:
√36 = √(6 x 6) = 6
Jadi, akar dari 36 adalah 6.
Contoh Soal 3: Tentukanlah akar dari 100
Cara Penyelesaian:
√100 = √(10 x 10) = 10
Jadi, akar dari 100 adalah 10.
Selain rumus bentuk akar, terdapat beberapa jenis bentuk akar yang sering digunakan dalam matematika. Berikut adalah jenis-jenis bentuk akar tersebut:
1. Akar kuadrat
Akar kuadrat adalah bentuk akar yang hasilnya sama dengan bilangan yang dipangkatkan dua kali. Misalnya, √25 = 5, karena 5^2 = 25.
2. Akar pangkat tiga
Akar pangkat tiga adalah bentuk akar yang hasilnya sama dengan bilangan yang dipangkatkan tiga kali. Misalnya, ∛27 = 3, karena 3^3 = 27.
3. Akar pangkat n
Akar pangkat n adalah bentuk akar yang hasilnya sama dengan bilangan yang dipangkatkan n kali. Misalnya, ∜16 = 2, karena 2^4 = 16.
Kesimpulan
Perpangkatan dan bentuk akar merupakan operasi matematika yang penting dalam pemecahan masalah yang melibatkan perhitungan kuadrat atau pangkat tertentu. Dalam perpangkatan, bilangan yang ingin dipangkatkan disebut sebagai basis dan pangkatnya disebut sebagai eksponen. Sedangkan dalam bentuk akar, bilangan yang ingin diakarkan ditulis dalam simbol akar. Dalam perhitungan perpangkatan maupun bentuk akar, rumus dan jenis-jenisnya perlu dipahami dengan baik untuk memperoleh hasil yang akurat.
 Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
