Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Daftar Isi
Pengertian Rumus Perkalian Matriks
Rumus perkalian matriks adalah salah satu konsep matematika dasar yang sangat penting dalam bidang aljabar linear. Perkalian matriks digunakan untuk mengalikan matriks satu dengan yang lain untuk mendapatkan hasil yang baru. Untuk mengalikan matriks, digunakan rumus perkalian matriks yang terdiri dari jumlah elemen-elemen matriks yang dikalikan. Rumus perkalian matriks sangat berguna dalam perhitungan matematika dan teknik, khususnya dalam pemrograman komputer.
Langkah-langkah Penyelesaian Rumus Perkalian Matriks
Untuk dapat mengalikan dua buah matriks, harus memperhatikan beberapa persyaratan terlebih dahulu. Persyaratan tersebut diantaranya adalah jumlah kolom pada matriks pertama harus sama dengan jumlah baris pada matriks kedua. Jika persyaratan tersebut sudah terpenuhi, maka dapat dilakukan langkah-langkah penyelesaian rumus perkalian matriks sebagai berikut:
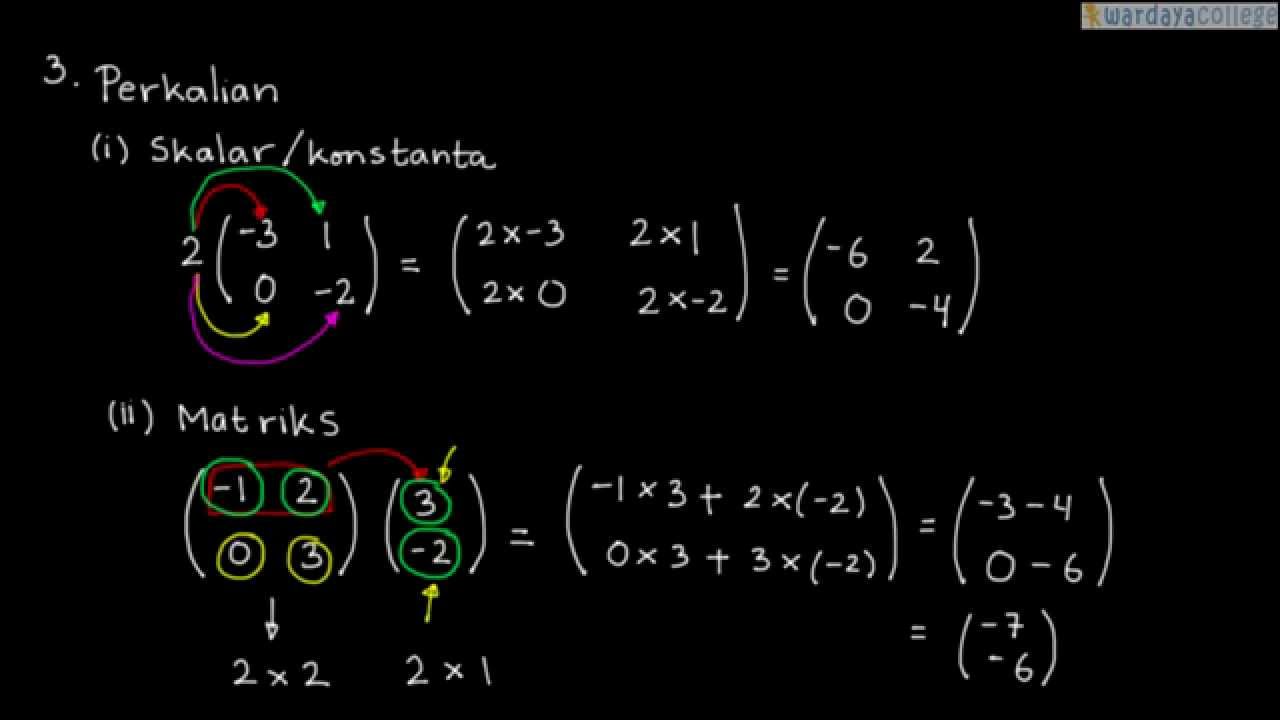
1. Tentukan matriks pertama dan kedua yang akan di kalikan
2. Tentukan jumlah baris dan kolom pada masing-masing matriks
3. Pastikan jumlah kolom pada matriks pertama sama dengan jumlah baris pada matriks kedua
4. Hitung perkalian dari setiap elemen pada masing-masing baris dan kolom pada kedua matriks
5. Jumlahkan hasil perkalian setiap elemen pada masing-masing baris dan kolom pada kedua matriks untuk mendapatkan hasil akhir
6. Simpan hasil akhir pada matriks baru sebagai hasil perkalian matriks
Contoh Soal dan Penyelesaian Rumus Perkalian Matriks
Berikut adalah contoh soal dan penyelesaian rumus perkalian matriks:
Diketahui matriks A = [3 5] dan matriks B = [ 2 4 6 ]. Hitunglah hasil perkalian matriks A dan B!
Penyelesaian:
Jumlah kolom pada matriks A adalah 1 dan jumlah baris pada matriks B adalah 1. Karena tidak memenuhi persyaratan, maka tidak dapat dilakukan perkalian matriks pada kedua matriks tersebut.
Diketahui matriks A = [1 2 3] dan matriks B = [ 4 5 6 ] serta matriks C = [ 7 8 ]. Hitunglah hasil perkalian matriks A dan B!
Penyelesaian:
Jumlah kolom pada matriks A adalah 3 dan jumlah baris pada matriks B adalah 1. Karena memenuhi persyaratan, maka dapat dilakukan perkalian matriks dengan mengikuti langkah-langkah sebagai berikut:
“`
[1 2 3] [4] [1*4 + 2*5 + 3*6] [32]
x [5] =
[6]
“`
Jumlahkan hasil perkalian setiap elemen pada masing-masing baris dan kolom pada kedua matriks untuk mendapatkan hasil akhir. Dalam contoh ini, hasil akhir dari perkalian matriks A dan B adalah [32].
Jumlah kolom pada matriks B adalah 3 dan jumlah baris pada matriks C adalah 1. Karena tidak memenuhi persyaratan, maka tidak dapat dilakukan perkalian matriks pada kedua matriks tersebut.
Persamaan Matriks
Selain rumus perkalian matriks, terdapat juga persamaan matriks yang dapat digunakan untuk menyelesaikan sistem persamaan linear. Persamaan matriks digunakan untuk menyederhanakan rumus perhitungan dengan menggunakan matriks. Persamaan matriks juga digunakan untuk menyelesaikan masalah matematika dalam bidang aljabar linear dan pemrograman komputer.
Cara Penyelesaian Persamaan Matriks
Untuk dapat menyelesaikan persamaan matriks, dapat dilakukan dengan beberapa cara. Cara-cara tersebut diantaranya adalah:
1. Metode eliminasi Gauss
2. Metode eliminasi Gauss-Jordan
3. Metode matriks balikan
4. Metode cramer
Metode Eliminasi Gauss
Metode eliminasi Gauss adalah salah satu cara untuk menyelesaikan persamaan matriks dengan cara mengubah matriks menjadi matriks segitiga atas tereduksi. Metode ini dilakukan dengan mengikuti langkah-langkah sebagai berikut:
1. Tentukan matriks koefisien dan matriks konstanta dari sistem persamaan linear
2. Ubah matriks koefisien menjadi matriks segitiga atas
3. Reduksi matriks segitiga atas menjadi matriks segitiga atas tereduksi
4. Dapatkan solusi persamaan dengan mencari nilai variabel pada matriks segitiga atas tereduksi
Contoh soal dan penyelesaian metode eliminasi Gauss:
Diketahui sistem persamaan linear berikut:
“`
2x + 4y + 6z = 22
3x + 5y + 7z = 31
4x + 6y + 8z = 40
“`
Penyelesaian:
1. Tentukan matriks koefisien dan matriks konstanta dari sistem persamaan linear
“`
[2 4 6] [22]
[3 5 7] x [31]
[4 6 8] [40]
“`
2. Ubah matriks koefisien menjadi matriks segitiga atas
“`
[2 4 6] [22]
[0 -2 -4] x [-13]
[0 0 0] [ 2]
“`
3. Reduksi matriks segitiga atas menjadi matriks segitiga atas tereduksi
“`
[2 4 6] [22]
[0 -2 -4] x [-13]
[0 0 0] [ 2]
[2 4 6] [22]
[0 -2 -4] x [-13]
[0 0 0] [ 2]
[2 4 6] [22]
[0 -2 -4] x [-13]
[0 0 0] [2]
[2 4 6] [22]
[0 -2 -4] x [-13]
[0 0 0] [2]
[2 4 6] [22]
[0 -2 -4] x [-13]
[0 0 0] [2]
“`
4. Dapatkan solusi persamaan dengan mencari nilai variabel pada matriks segitiga atas tereduksi
“`
2x + 4y + 6z = 22
-2y – 4z = -13
0 = 2
“`
Dari hasil di atas, dapat dilihat bahwa persamaan tidak memiliki solusi karena terdapat nilai yang bertentangan dengan logika matematika.
Metode Eliminasi Gauss-Jordan
Metode eliminasi Gauss-Jordan adalah salah satu cara untuk menyelesaikan persamaan matriks dengan cara mengubah matriks menjadi matriks segitiga atas tereduksi. Metode ini dilakukan dengan mengikuti langkah-langkah sebagai berikut:
1. Tentukan matriks koefisien dan matriks konstanta dari sistem persamaan linear
2. Ubah matriks koefisien menjadi matriks segitiga atas tereduksi
3. Dapatkan solusi persamaan dengan mencari nilai variabel pada matriks segitiga atas tereduksi
Contoh soal dan penyelesaian metode eliminasi Gauss-Jordan:
Diketahui sistem persamaan linear berikut:
“`
2x + 4y + 6z = 22
3x + 5y + 7z = 31
4x + 6y + 8z = 40
“`
Penyelesaian:
1. Tentukan matriks koefisien dan matriks konstanta dari sistem persamaan linear
“`
[2 4 6] [22]
[3 5 7] x [31]
[4 6 8] [40]
“`
2. Ubah matriks koef
