Daftar Isi
Rumus Luas Tabung
Tabung merupakan bangun ruang yang memiliki bentuk silinder dengan dua buah tutup pada kedua ujungnya. Luas tabung adalah salah satu hal penting yang harus diketahui untuk menghitung berbagai hal, seperti volume atau kapasitas isi tabung. Rumus luas tabung terdiri dari dua bagian, yaitu luas alas dan luas selimut.
Luas Alas Tabung
Luas alas tabung adalah luas lingkaran yang terdapat pada salah satu ujung tabung. Rumus luas alas tabung adalah sebagai berikut:
L = πr^2
Keterangan:
L = luas alas tabung
π = 3,14 (konstanta pi)
r = jari-jari alas tabung
Untuk menghitung luas alas tabung, pertama-tama kita perlu mengetahui jari-jari alas tabung. Jika jari-jari alas tabung diketahui, maka kita bisa langsung menghitung luas alas dengan mengikuti rumus di atas.
Contoh Soal:
Sebuah tabung memiliki jari-jari 7 cm. Tentukan luas alas dari tabung tersebut!
Penyelesaian:
L = πr^2
L = 3,14 x 7^2
L = 153,86 cm^2
Jadi, luas alas tabung tersebut adalah 153,86 cm^2.
Luas Selimut Tabung
Luas selimut tabung adalah luas permukaan tabung yang terletak di antara kedua buah tutup tabung. Rumus luas selimut tabung adalah sebagai berikut:
L = 2πrh
Keterangan:
L = luas selimut tabung
π = 3,14 (konstanta pi)
r = jari-jari alas tabung
h = tinggi tabung
Untuk menghitung luas selimut tabung, kita perlu mengetahui jari-jari alas tabung dan tinggi tabung. Jika kedua nilai tersebut sudah diketahui, kita bisa langsung menghitung luas selimut dengan rumus di atas.
Contoh Soal:
Sebuah tabung memiliki jari-jari 3 cm dan tinggi 10 cm. Tentukan luas selimut dari tabung tersebut!
Penyelesaian:
L = 2πrh
L = 2 x 3,14 x 3 x 10
L = 188,4 cm^2
Jadi, luas selimut tabung tersebut adalah 188,4 cm^2.
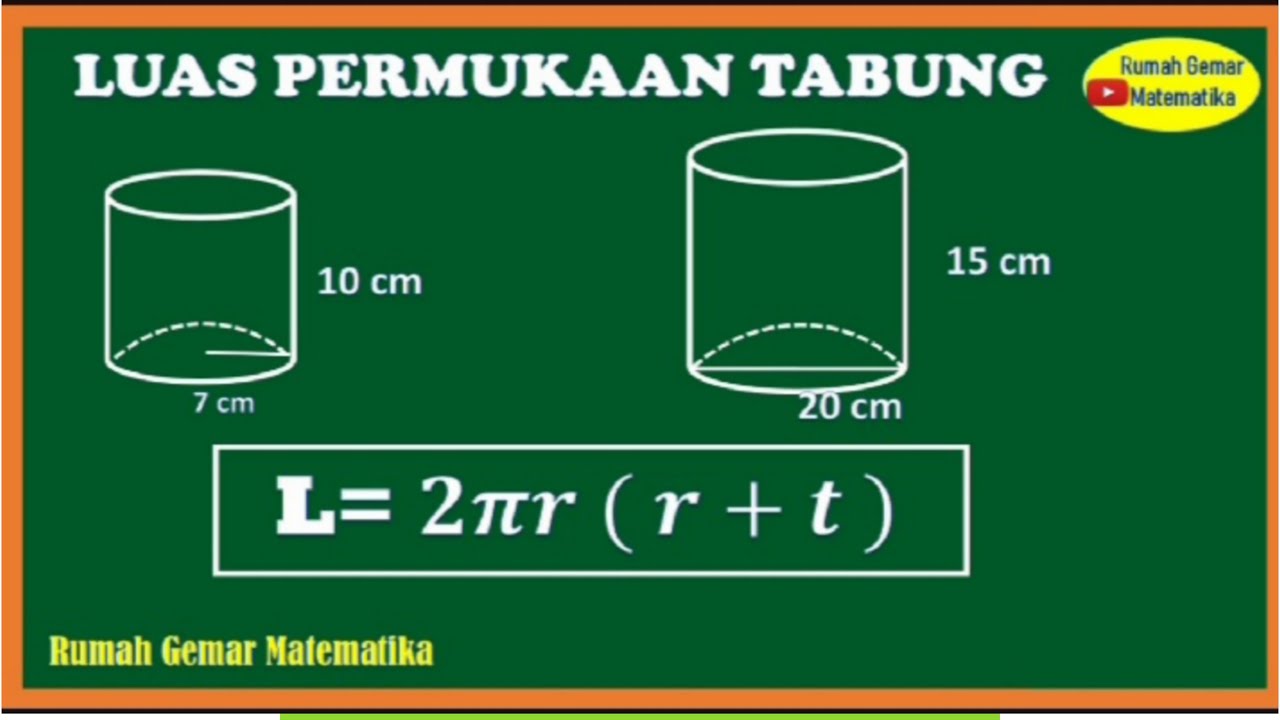
Luas Permukaan Tabung
Luas permukaan tabung adalah gabungan dari luas alas dan luas selimut. Rumus luas permukaan tabung adalah sebagai berikut:
L = 2πr(r + h)
Keterangan:
L = luas permukaan tabung
π = 3,14 (konstanta pi)
r = jari-jari alas tabung
h = tinggi tabung
Untuk menghitung luas permukaan tabung, kita perlu mengetahui jari-jari alas dan tinggi tabung. Jika kedua nilai tersebut sudah diketahui, kita bisa langsung menghitung luas permukaan dengan rumus di atas.
Contoh Soal:
Sebuah tabung memiliki jari-jari 5 cm dan tinggi 8 cm. Tentukan luas permukaan dari tabung tersebut!
Penyelesaian:
L = 2πr(r + h)
L = 2 x 3,14 x 5(5 + 8)
L = 314 cm^2
Jadi, luas permukaan tabung tersebut adalah 314 cm^2.
Kesimpulan
Tabung adalah bangun ruang yang memiliki bentuk silinder dengan dua buah tutup pada kedua ujungnya. Luas tabung terdiri dari dua bagian, yaitu luas alas dan luas selimut. Luas alas tabung adalah luas lingkaran yang terdapat pada salah satu ujung tabung, sedangkan luas selimut tabung adalah luas permukaan tabung yang terletak di antara kedua buah tutup tabung. Luas permukaan tabung adalah gabungan dari luas alas dan luas selimut. Rumus luas tabung dapat digunakan untuk menghitung berbagai hal, seperti volume atau kapasitas isi tabung.
 Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
