Belajar Rumus Luas Permukaan Dan Volume Bangun Ruang: Pahami Konsep Dan Contohnya Dengan Mudah

Rumus Luas Permukaan Dan Volume Bangun Ruang

Bangun ruang adalah bentuk geometri tiga dimensi yang memiliki sisi, sudut, dan ruang. Dalam geometri, kita mengenal beberapa bangun ruang seperti kubus, balok, prisma, tabung, kerucut, dan bola. Setiap bangun ruang memiliki rumus luas permukaan dan volume yang berbeda. Di dalam artikel ini, kita akan membahas rumus luas permukaan dan volume dari setiap bangun ruang.

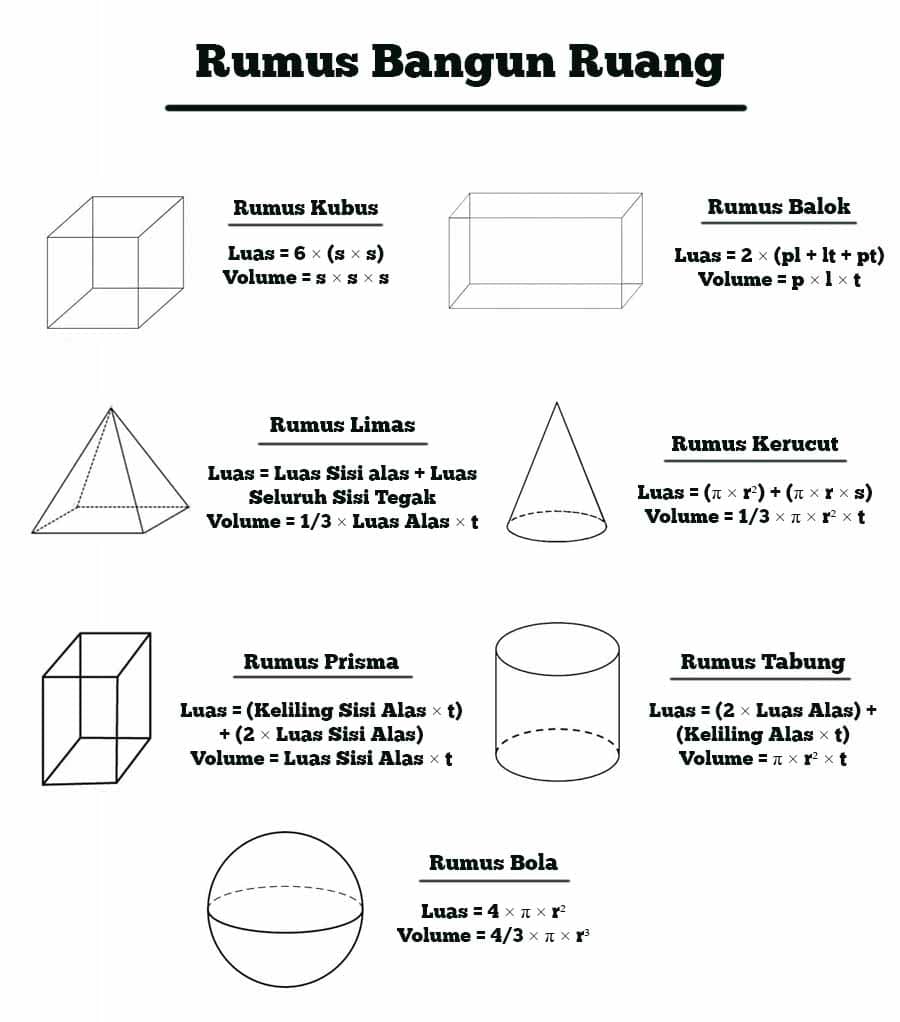
1. Rumus Luas Permukaan Kubus

Kubus adalah bangun ruang yang memiliki enam sisi yang sama besar dan bentuknya seperti kubus. Untuk menghitung luas permukaan kubus, kita hanya perlu mengalikan panjang sisi dengan enam.

Rumus luas permukaan kubus adalah L = 6s²
Keterangan:
L = Luas Permukaan Kubus
s = Panjang Sisi

Contoh soal:
Sebuah kubus memiliki panjang sisi sebesar 5 cm, maka luas permukaan kubus tersebut adalah:
L = 6 x 5²
L = 6 x 25
L = 150 cm²

2. Rumus Volume Kubus

Untuk menghitung volume kubus, kita hanya perlu mengalikan panjang sisi dengan tiga.

Rumus volume kubus adalah V = s³
Keterangan:
V = Volume Kubus
s = Panjang Sisi

Contoh soal:
Sebuah kubus memiliki panjang sisi sebesar 5 cm, maka volume kubus tersebut adalah:
V = 5³
V = 5 x 5 x 5
V = 125 cm³

3. Rumus Luas Permukaan Balok

Balok adalah bangun ruang yang memiliki enam sisi dan bentuknya seperti kotak panjang. Untuk menghitung luas permukaan balok, kita perlu mengalikan panjang, lebar, dan tinggi dengan dua kemudian menjumlahkannya.

Rumus luas permukaan balok adalah L = 2(pl + pt + lt)
Keterangan:
L = Luas Permukaan Balok
p = Panjang
l = Lebar
t = Tinggi

Contoh soal:
Sebuah balok memiliki panjang 8 cm, lebar 5 cm, dan tinggi 6 cm, maka luas permukaan balok tersebut adalah:
L = 2(8×5 + 8×6 + 5×6)
L = 2(40 + 48 + 30)
L = 2 x 118
L = 236 cm²

4. Rumus Volume Balok

Untuk menghitung volume balok, kita hanya perlu mengalikan panjang, lebar, dan tinggi.

Rumus volume balok adalah V = p x l x t
Keterangan:
V = Volume Balok
p = Panjang
l = Lebar
t = Tinggi

Contoh soal:
Sebuah balok memiliki panjang 8 cm, lebar 5 cm, dan tinggi 6 cm, maka volume balok tersebut adalah:
V = 8 x 5 x 6
V = 240 cm³

5. Rumus Luas Permukaan Prisma

Prisma adalah bangun ruang yang memiliki dua sisi segitiga atau sisi persegi panjang dan bentuknya seperti segitiga atau persegi panjang. Untuk menghitung luas permukaan prisma, kita perlu mengalikan luas alas dengan dua kemudian menambahkannya dengan keliling alas dikalikan tinggi.

Rumus luas permukaan prisma adalah L = 2A + lp
Keterangan:
L = Luas Permukaan Prisma
A = Luas Alas
l = Keliling Alas
p = Tinggi

Contoh soal:
Sebuah prisma segitiga memiliki alas dengan panjang 6 cm, lebar 10 cm, dan tinggi 8 cm. Hitunglah luas permukaan prisma tersebut.
A = ½ x 6 x 10
A = 30 cm²
l = 6 + 10 + √(6² + 10²)
l = 6 + 10 + √136
l = 6 + 10 + 11.66
l = 27.66 cm
L = 2A + lp
L = 2(30) + 27.66(8)
L = 60 + 220.88
L = 280.88 cm²

6. Rumus Volume Prisma

Untuk menghitung volume prisma, kita hanya perlu mengalikan luas alas dengan tinggi.

Rumus volume prisma adalah V = A x p
Keterangan:
V = Volume Prisma
A = Luas Alas
p = Tinggi

Contoh soal:
Sebuah prisma segitiga memiliki alas dengan panjang 6 cm, lebar 10 cm, dan tinggi 8 cm. Hitunglah volume prisma tersebut.
A = ½ x 6 x 10
A = 30 cm²
V = A x p
V = 30 x 8
V = 240 cm³

7. Rumus Luas Permukaan Tabung

Tabung adalah bangun ruang yang memiliki alas lingkaran dan bentuknya seperti silinder. Untuk menghitung luas permukaan tabung, kita perlu mengalikan keliling lingkaran alas dengan tinggi, kemudian ditambahkan dengan dua kali luas lingkaran alas.

Rumus luas permukaan tabung adalah L = 2πr² + 2πrt
Keterangan:
L = Luas Permukaan Tabung
r = Jari-jari Alas
t = Tinggi

Contoh soal:
Sebuah tabung memiliki jari-jari 4 cm dan tinggi 10 cm. Hitunglah luas permukaan tabung tersebut.
L = 2πr² + 2πrt
L = 2π(4)² + 2π(4)(10)
L = 2π(16) + 2π(40)
L = 32π + 80π
L = 112π cm²
L = 352.8 cm² (diambil π = 22/7)

8. Rumus Volume Tabung

Untuk menghitung volume tabung, kita hanya perlu mengalikan luas alas dengan tinggi.

Rumus volume tabung adalah V = πr²t
Keterangan:
V = Volume Tabung
r = Jari-jari Alas
t = Tinggi

Contoh soal:
Sebuah tabung memiliki jari-jari 4 cm dan tinggi 10 cm. Hitunglah volume tabung tersebut.
V = πr²t
V = π(4)²(10)
V = 160π cm³
V = 502.4 cm³ (diambil π = 22/7)

9. Rumus Luas Permukaan Kerucut

Kerucut adalah bangun ruang yang memiliki alas lingkaran dan titik puncak yang berada di atas alas. Untuk menghitung luas permukaan kerucut, kita perlu menghitung luas selimut kerucut dan ditambahkan dengan luas lingkaran alas.

Rumus luas permukaan kerucut adalah L = πr² + πrl
Keterangan:
L = Luas Permukaan Kerucut
r = Jari-jari Alas
l = Garis Pelukis

Contoh soal:
Sebuah kerucut memiliki jari-jari 6 cm, garis pelukis 10 cm, dan tinggi 8 cm. Hitunglah luas permukaan kerucut tersebut.
L = πr² + πrl
L = π(6)² + π(6)(10)
L = π(36) + π(60)
L = 96π cm²
L = 301.4 cm² (diambil π = 22/7)

10. Rumus Volume Kerucut

Untuk menghitung volume kerucut, kita hanya perlu mengalikan luas alas dengan tinggi, kemudian dibagi tiga.

Rumus volume kerucut adalah V = 1/3πr²t
Keterangan:
V = Volume Kerucut
r = Jari-jari Alas
t = Tinggi

Contoh soal:
Sebuah kerucut memiliki jari-jari 6 cm dan tinggi 8 cm. Hitunglah volume kerucut tersebut.
V = 1/3πr²t
V = 1/3π(6)²(8)
V = 1/3π(36)(8)
V = 1/3π(288)
V = 96π cm³
V = 301.4 cm³ (diambil π = 22/7)

11. Rumus Luas Permukaan Bola

Bola adalah bangun ruang yang memiliki semua titik pada permukaannya sama jaraknya dari titik pusat. Untuk menghitung luas permukaan bola