Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Daftar Isi
Pengertian Rumus Bangun Ruang Sisi Datar
Rumus Bangun Ruang Sisi Datar adalah rumus yang digunakan untuk menghitung luas permukaan bangun ruang yang terdiri dari sisi datar. Sisi datar atau permukaan datar adalah bagian-bagian dari permukaan bangun ruang yang tidak melengkung. Perhitungan Rumus Bangun Ruang Sisi Datar sangat penting terutama dalam perencanaan dan perhitungan luas bidang-bidang pada bangun ruang. Dalam rumus ini, dihitung luaslah permukaan bangun ruang tersebut dan merupakan hasil kali dari panjang dan lebar bidang datar pada bangun ruang tersebut.
Bangun Ruang Sisi Datar yang Umum
Ada beberapa jenis bangun ruang yang memiliki sisi datar, di antaranya adalah sebagai berikut:
Kubus
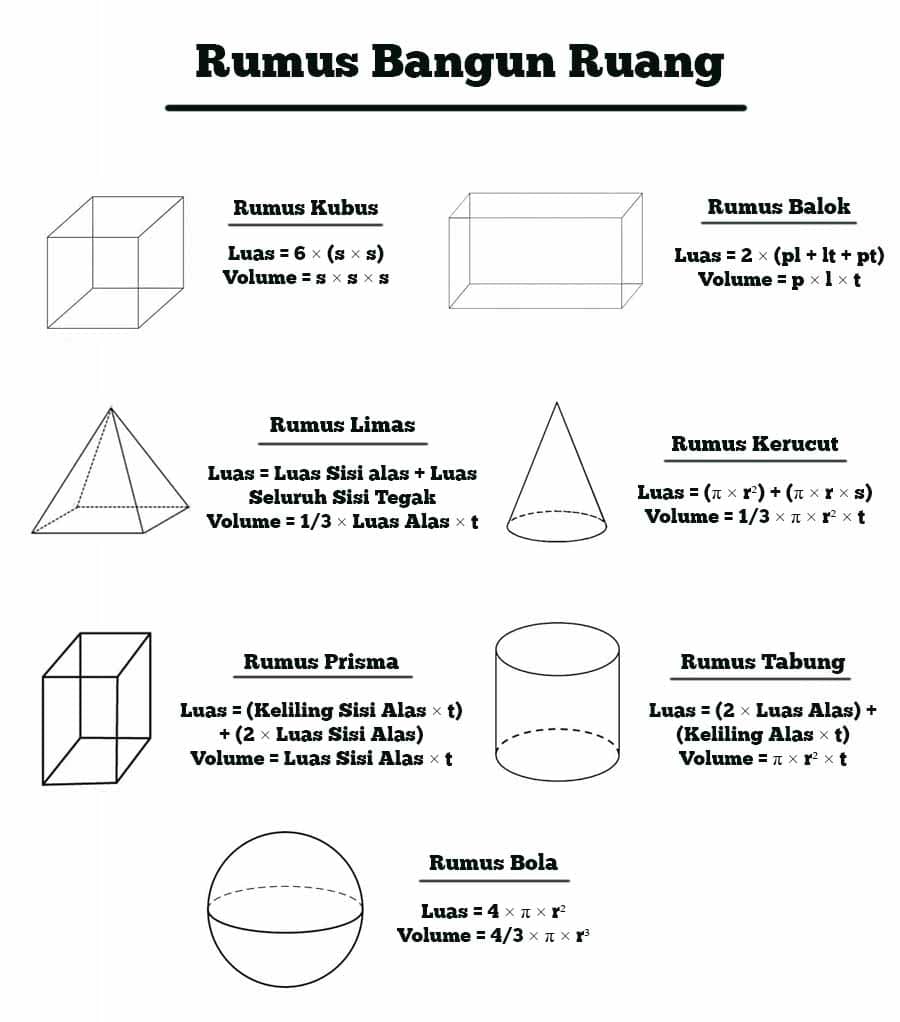
Kubus adalah bangun ruang tiga dimensi yang terdiri dari enam sisi datar yang sama. Setiap sisi kubus berbentuk persegi dengan ukuran yang sama. Rumus untuk menghitung luas permukaan kubus adalah sebagai berikut:
Luas permukaan kubus = 6 × sisi × sisi
Balok
Balok adalah bangun ruang tiga dimensi yang juga memiliki enam sisi datar. Namun, sisi-sisi yang bersebrangan pada balok memiliki ukuran yang sama. Rumus untuk menghitung luas permukaan balok adalah sebagai berikut:
Luas permukaan balok = 2 × (panjang × lebar + panjang × tinggi + lebar × tinggi)
Prisma
Prisma adalah bangun ruang yang memiliki dua sisi datar yang sama dan sisi-sisi tegak berbentuk segi banyak. Rumus untuk menghitung luas permukaan prisma adalah sebagai berikut:
Luas permukaan prisma = keliling alas × tinggi + 2 × luas alas
Tabung
Tabung adalah bangun ruang tiga dimensi yang memiliki dua sisi datar yang berbentuk lingkaran dengan ukuran yang sama dan satu sisi melengkung. Rumus untuk menghitung luas permukaan tabung adalah sebagai berikut:
Luas permukaan tabung = 2 × luas lingkaran alas + keliling lingkaran alas × tinggi
Bola
Bola adalah bangun ruang tiga dimensi yang tidak memiliki sisi datar. Namun, untuk menghitung luas permukaan bola, kita dapat menggunakan rumus sebagai berikut:
Luas permukaan bola = 4 × π × jari-jari²
Cara Menghitung Rumus Bangun Ruang Sisi Datar
Untuk menghitung rumus bangun ruang sisi datar, ada beberapa langkah yang harus dilakukan, yaitu sebagai berikut:
1. Tentukan Bangun Ruang yang Akan Dihitung
Pertama-tama, tentukanlah bangun ruang yang akan dihitung luas permukaannya. Pastikan bahwa bangun ruang tersebut memiliki sisi datar yang dapat dihitung luas permukaannya.
2. Tentukan Ukuran Sisi-Sisi Datar
Setelah menentukan bangun ruang yang akan dihitung, selanjutnya tentukan ukuran dari sisi-sisi datar yang ada pada bangun ruang tersebut. Ukuran tersebut dapat berupa panjang dan lebar atau jari-jari lingkaran.
3. Gunakan Rumus yang Sesuai
Setelah menentukan ukuran sisi-sisi datar, selanjutnya gunakan rumus yang sesuai untuk menghitung luas permukaan bangun ruang tersebut.
4. Hitunglah Hasilnya
Setelah mengetahui rumus yang harus digunakan, selanjutnya hitunglah hasilnya dengan memasukkan nilai ukuran sisi-sisi datar yang sudah ditentukan pada rumus yang digunakan.
Contoh Soal Rumus Bangun Ruang Sisi Datar
Untuk memahami penggunaan Rumus Bangun Ruang Sisi Datar, berikut adalah beberapa contoh soal dan cara penyelesaiannya:
Contoh Soal 1
Sebuah kubus memiliki sisi sepanjang 6 cm. Berapa luas permukaan kubus tersebut?
Penyelesaian
Luas permukaan kubus = 6 × sisi × sisi
Luas permukaan kubus = 6 × 6 cm × 6 cm
Luas permukaan kubus = 216 cm²
Jadi, luas permukaan kubus tersebut adalah 216 cm².
Contoh Soal 2
Sebuah balok memiliki panjang 8 cm, lebar 4 cm, dan tinggi 6 cm. Berapa luas permukaan balok tersebut?
Penyelesaian
Luas permukaan balok = 2 × (panjang × lebar + panjang × tinggi + lebar × tinggi)
Luas permukaan balok = 2 × (8 cm × 4 cm + 8 cm × 6 cm + 4 cm × 6 cm)
Luas permukaan balok = 2 × (32 cm² + 48 cm² + 24 cm²)
Luas permukaan balok = 2 × 104 cm²
Luas permukaan balok = 208 cm²
Jadi, luas permukaan balok tersebut adalah 208 cm².
Contoh Soal 3
Sebuah prisma segitiga memiliki alas segitiga dengan panjang sisi-sisi 5 cm, 8 cm, dan 7 cm. Tinggi prisma tersebut adalah 10 cm. Berapa luas permukaan prisma tersebut?
Penyelesaian
Luas permukaan prisma = keliling alas × tinggi + 2 × luas alas
Keliling alas = 5 cm + 8 cm + 7 cm
Keliling alas = 20 cm
Luas alas = 1/2 × alas × tinggi
Luas alas = 1/2 × (5 cm × 10 cm)
Luas alas = 25 cm²
Luas permukaan prisma = 20 cm × 10 cm + 2 × 25 cm²
Luas permukaan prisma = 200 cm² + 50 cm²
Luas permukaan prisma = 250 cm²
Jadi, luas permukaan prisma tersebut adalah 250 cm².
Contoh Soal 4
Sebuah tabung memiliki jari-jari 4 cm dan tinggi 10 cm. Berapa luas permukaan tabung tersebut?
Penyelesaian
Luas permukaan tabung = 2 × luas lingkaran alas + keliling lingkaran alas × tinggi
Luas lingkaran alas = π × jari-jari²
Luas lingkaran alas = π × 4 cm²
Luas lingkaran alas = 16 π cm²
Keliling lingkaran alas = 2 × π × jari-jari
Keliling lingkaran alas = 2 × π × 4 cm
Keliling lingkaran alas = 8 π cm
Luas permukaan tabung = 2 × 16 π cm² + 8 π cm × 10 cm
Luas permukaan tabung = 32 π cm² + 80 π cm²
Luas permukaan tabung = 112 π cm²
Luas permukaan tabung ≈ 351,86 cm²
Jadi, luas permukaan tabung tersebut adalah sekitar 351,86 cm².
Kesimpulan
Rumus Bangun Ruang Sisi Datar digunakan untuk menghitung luas permukaan bangun ruang yang terdiri dari sisi datar. Ada beberapa jenis bangun ruang yang memiliki sisi datar, di antaranya adalah kubus, balok, prisma, tabung, dan bola. Untuk menghitung rumus bangun ruang sisi datar, perlu dilakukan beberapa langkah, yaitu menentukan bangun ruang yang akan dihitung, menentukan ukuran sisi-sisi datar, menggunakan rumus yang sesuai, dan menghitung hasilnya. Dalam penggunaannya, penting untuk memahami konsep dan rumus yang digunakan agar dapat menyelesaikan perhitungan dengan tepat dan akurat.
