Memahami Pembuktian Teorema Pythagoras Dengan Metode Geometri

Pengenalan

Teorema Pythagoras adalah salah satu teorema matematika yang paling terkenal dan penting. Teorema ini menyatakan bahwa dalam sebuah segitiga siku-siku, jumlah kuadrat dari kedua sisi yang pendek sama dengan kuadrat dari sisi miring. Teorema Pythagoras sangat penting dalam matematika, fisika, astronomi, dan banyak bidang lainnya. Di dalam tulisan ini, kita akan membahas pembuktian Teorema Pythagoras.

Asal Usul Teorema Pythagoras

Teorema Pythagoras diberi nama sesuai dengan matematikawan Yunani kuno, Pythagoras. Namun, teorema ini sebenarnya sudah dikenal sejak zaman kuno di Mesir, Babilonia, India, dan Cina. Pythagoras menciptakan pembuktian yang terkenal dan paling dikenal saat ini.

Pembuktian Pertama

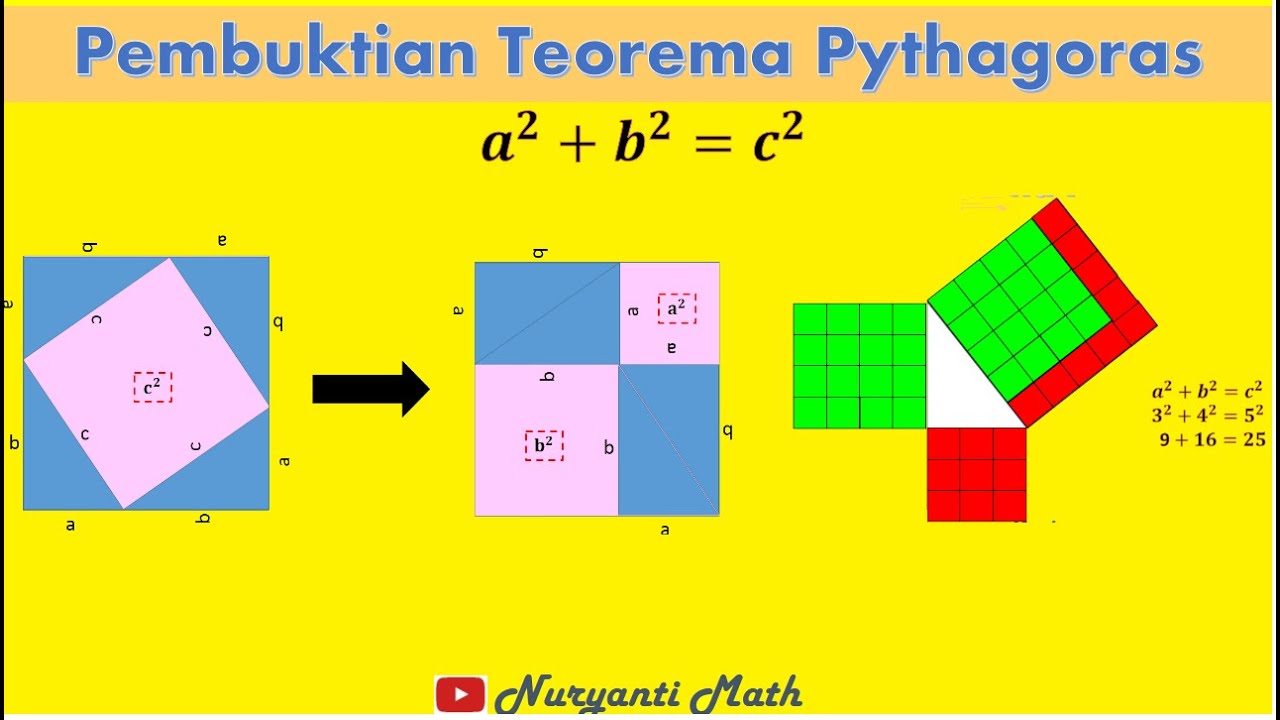
Pembuktian pertama teorema Pythagoras dikembangkan oleh ahli matematika India, Baudhayana pada abad ke-6 SM. Pembuktian ini menggunakan prinsip dasar geometri, yaitu bahwa segitiga dengan sisi yang sama dan sudut yang sama akan sama besar. Pembuktian ini melibatkan dua segitiga siku-siku yang dibentuk oleh garis-garis yang ditarik pada sisi-sisi segitiga asli. Dalam pembuktian ini, kita dapat menghitung luas kedua segitiga dan membandingkannya untuk membuktikan teorema Pythagoras.

Pembuktian Kedua

Pembuktian kedua teorema Pythagoras dikembangkan oleh Euclid pada abad ke-3 SM. Euclid menggunakan prinsip dasar geometri, yaitu bahwa rasio antara sisi-sisi segitiga siku-siku adalah konstan. Dalam pembuktian ini, Euclid menggambar sebuah kuadrat di setiap sisi segitiga dan menunjukkan bahwa jumlah luas kedua kuadrat pada sisi yang pendek sama dengan luas kuadrat pada sisi miring. Pembuktian ini dianggap sebagai pembuktian yang sangat elegan dan disukai oleh banyak matematikawan.

Pembuktian Ketiga

Pembuktian ketiga teorema Pythagoras dikembangkan oleh matematikawan Persia, Abu Ja’far Muhammad ibn Musa al-Khwarizmi pada abad ke-9 Masehi. Pembuktian ini menggunakan prinsip dasar aljabar, yaitu bahwa jika dua bilangan sama dengan bilangan ketiga, maka kuadrat dari dua bilangan tersebut sama dengan jumlah kuadrat dari bilangan ketiga. Dalam pembuktian ini, kita dapat mengalikan sisi-sisi segitiga dengan dirinya sendiri dan menunjukkan bahwa jumlah kuadrat dari dua sisi yang pendek sama dengan kuadrat dari sisi miring.

Pembuktian Keempat

Pembuktian keempat teorema Pythagoras dikembangkan oleh matematikawan Jerman, Johannes Kepler pada abad ke-17 Masehi. Pembuktian ini menggunakan prinsip dasar trigonometri, yaitu bahwa rasio antara sisi dan sudut segitiga adalah konstan. Dalam pembuktian ini, kita dapat menggambar sebuah lingkaran dengan diameter sama dengan sisi miring segitiga dan menunjukkan bahwa rasio antara sisi-sisi segitiga dan diameter lingkaran adalah konstan. Dengan menggunakan trigonometri, kita dapat menunjukkan bahwa jumlah kuadrat dari kedua sisi yang pendek sama dengan kuadrat dari sisi miring.

Pembuktian Kelima

Pembuktian kelima teorema Pythagoras dikembangkan oleh matematikawan Inggris, James A. Garfield pada abad ke-19 Masehi. Pembuktian ini menggunakan prinsip dasar aljabar, yaitu bahwa setiap bilangan bulat dapat diekspresikan sebagai jumlah dari kuadrat bilangan-bilangan bulat yang lebih kecil. Dalam pembuktian ini, kita dapat menunjukkan bahwa sisi-sisi segitiga siku-siku dapat diekspresikan sebagai jumlah dari kuadrat bilangan bulat yang lebih kecil. Dengan menggunakan aljabar, kita dapat menunjukkan bahwa jumlah kuadrat dari kedua sisi yang pendek sama dengan kuadrat dari sisi miring.

Kesimpulan

Teorema Pythagoras adalah salah satu teorema paling terkenal dan penting dalam matematika. Teorema ini telah dikenal sejak zaman kuno dan telah dibuktikan dengan berbagai cara oleh banyak ahli matematika terkenal. Pembuktian Teorema Pythagoras menggunakan prinsip dasar geometri, aljabar, dan trigonometri. Setiap metode pembuktian memiliki kelebihan dan kekurangan masing-masing, tetapi semua pembuktian menunjukkan bahwa teorema Pythagoras benar. Teorema Pythagoras memiliki banyak aplikasi dalam berbagai bidang, termasuk matematika, fisika, astronomi, dan teknik.