Daftar Isi
Cara Menghitung Volume Bangun Ruang
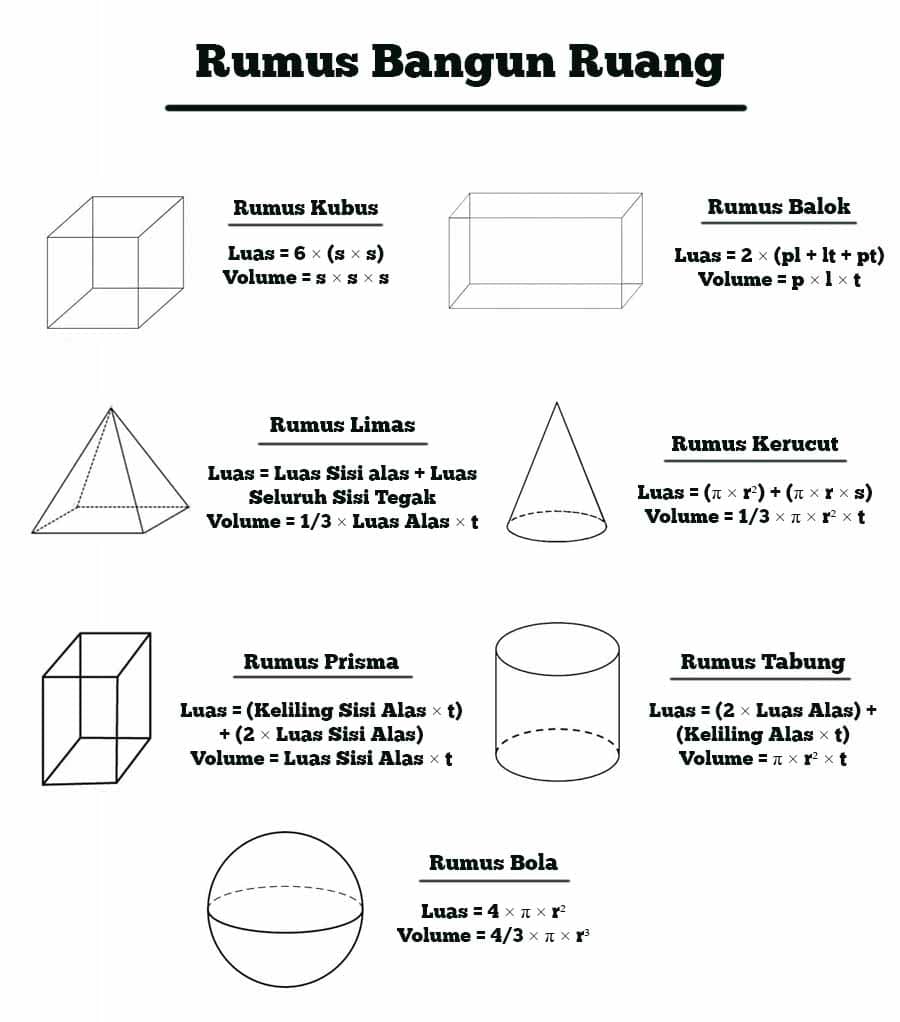
Bangun ruang adalah benda yang memiliki volume. Dalam kehidupan sehari-hari, kita seringkali dihadapkan dengan berbagai macam bangun ruang seperti bola, kubus, tabung, dan sebagainya. Untuk menghitung volume bangun ruang, terdapat rumus yang harus dipahami dan diaplikasikan. Berikut adalah beberapa langkah-langkah dalam cara menghitung volume bangun ruang.
I. Bola
Bola adalah bangun ruang yang berbentuk bulat sempurna. Volume bola dapat dihitung dengan menggunakan rumus:
V = 4/3πr^3
dimana V adalah volume, π adalah nilai pi (3.14), dan r adalah jari-jari bola.
Langkah-langkah untuk menghitung volume bola adalah sebagai berikut:
1. Tentukan jari-jari bola
Jari-jari bola adalah jarak dari pusat bola ke permukaannya. Jika jari-jari bola sudah diketahui, maka dapat langsung digunakan dalam rumus untuk menghitung volume.
2. Hitung volume bola
Setelah jari-jari bola diketahui, masukkan nilai r ke dalam rumus V = 4/3πr^3. Hitung dengan menggunakan kalkulator, dan hasilnya adalah volume bola.
Contoh Soal Bola:
Sebuah bola memiliki jari-jari 7 cm. Hitunglah volume bola tersebut.
Solusi:
V = 4/3πr^3
V = 4/3 x 3.14 x 7^3
V = 1436.76 cm^3
Jadi, volume bola tersebut adalah 1436.76 cm^3.
II. Kubus
Kubus adalah bangun ruang yang memiliki enam sisi yang sama besar dan berbentuk persegi. Volume kubus dapat dihitung dengan menggunakan rumus:
V = s^3
dimana V adalah volume dan s adalah panjang sisi kubus.
Langkah-langkah untuk menghitung volume kubus adalah sebagai berikut:
1. Tentukan panjang sisi kubus
Panjang sisi kubus adalah jarak antara dua titik pada sisi kubus yang berdekatan. Jika panjang sisi kubus sudah diketahui, maka dapat langsung digunakan dalam rumus untuk menghitung volume.
2. Hitung volume kubus
Setelah panjang sisi kubus diketahui, masukkan nilai s ke dalam rumus V = s^3. Hitung dengan menggunakan kalkulator, dan hasilnya adalah volume kubus.
Contoh Soal Kubus:
Sebuah kubus memiliki panjang sisi 5 cm. Hitunglah volume kubus tersebut.
Solusi:
V = s^3
V = 5^3
V = 125 cm^3
Jadi, volume kubus tersebut adalah 125 cm^3.
III. Tabung
Tabung adalah bangun ruang yang memiliki dua lingkaran sama besar sebagai alasnya dan sebuah selimut yang menutupi kedua lingkaran tersebut. Volume tabung dapat dihitung dengan menggunakan rumus:
V = πr^2t
dimana V adalah volume, π adalah nilai pi (3.14), r adalah jari-jari tabung, dan t adalah tinggi tabung.
Langkah-langkah untuk menghitung volume tabung adalah sebagai berikut:
1. Tentukan jari-jari dan tinggi tabung
Jari-jari tabung adalah jarak dari pusat lingkaran alas ke tepi lingkaran. Tinggi tabung adalah jarak antara dua lingkaran alas. Jika jari-jari dan tinggi tabung sudah diketahui, maka dapat langsung digunakan dalam rumus untuk menghitung volume.
2. Hitung volume tabung
Setelah jari-jari dan tinggi tabung diketahui, masukkan nilai r dan t ke dalam rumus V = πr^2t. Hitung dengan menggunakan kalkulator, dan hasilnya adalah volume tabung.
Contoh Soal Tabung:
Sebuah tabung memiliki jari-jari 4 cm dan tinggi 10 cm. Hitunglah volume tabung tersebut.
Solusi:
V = πr^2t
V = 3.14 x 4^2 x 10
V = 502.4 cm^3
Jadi, volume tabung tersebut adalah 502.4 cm^3.
IV. Prisma Segitiga
Prisma segitiga adalah bangun ruang yang memiliki dua alas segitiga dan tiga sisi berbentuk persegi. Volume prisma segitiga dapat dihitung dengan menggunakan rumus:
V = Luas alas x Tinggi
dimana V adalah volume, Luas alas adalah luas segitiga, dan Tinggi adalah tinggi prisma.
Langkah-langkah untuk menghitung volume prisma segitiga adalah sebagai berikut:
1. Tentukan luas alas prisma segitiga
Luas alas prisma segitiga adalah setengah dari hasil perkalian alas dan tinggi segitiga. Jika luas alas prisma segitiga sudah diketahui, maka dapat langsung digunakan dalam rumus untuk menghitung volume.
2. Tentukan tinggi prisma segitiga
Tinggi prisma segitiga adalah jarak antara kedua alas segitiga. Jika tinggi prisma segitiga sudah diketahui, maka dapat langsung digunakan dalam rumus untuk menghitung volume.
3. Hitung volume prisma segitiga
Setelah luas alas dan tinggi prisma segitiga diketahui, masukkan nilai Luas alas dan Tinggi ke dalam rumus V = Luas alas x Tinggi. Hitung dengan menggunakan kalkulator, dan hasilnya adalah volume prisma segitiga.
Contoh Soal Prisma Segitiga:
Sebuah prisma segitiga memiliki alas segitiga dengan panjang 10 cm dan tinggi 6 cm. Tinggi prisma adalah 8 cm. Hitunglah volume prisma segitiga tersebut.
Solusi:
Luas alas = 1/2 x alas x tinggi
Luas alas = 1/2 x 10 x 6
Luas alas = 30 cm^2
V = Luas alas x Tinggi
V = 30 x 8
V = 240 cm^3
Jadi, volume prisma segitiga tersebut adalah 240 cm^3.
V. Limas Segitiga
Limas segitiga adalah bangun ruang yang memiliki alas segitiga dan tiga sisi berbentuk segitiga. Volume limas segitiga dapat dihitung dengan menggunakan rumus:
V = 1/3 x Luas alas x Tinggi
dimana V adalah volume, Luas alas adalah luas segitiga, dan Tinggi adalah tinggi limas.
Langkah-langkah untuk menghitung volume limas segitiga adalah sebagai berikut:
1. Tentukan luas alas limas segitiga
Luas alas limas segitiga adalah setengah dari hasil perkalian alas dan tinggi segitiga. Jika luas alas limas segitiga sudah diketahui, maka dapat langsung digunakan dalam rumus untuk menghitung volume.
2. Tentukan tinggi limas segitiga
Tinggi limas segitiga adalah jarak antara titik puncak limas dan alas segitiga. Jika tinggi limas segitiga sudah diketahui, maka dapat langsung digunakan dalam rumus untuk menghitung volume.
3. Hitung volume limas segitiga
Setelah luas alas dan tinggi limas segitiga diketahui, masukkan nilai Luas alas dan Tinggi ke dalam rumus V = 1/3 x Luas alas x Tinggi. Hitung dengan menggunakan kalkulator, dan hasilnya adalah volume limas segitiga.
Contoh Soal Limas Segitiga:
Sebuah limas segitiga memiliki alas segitiga dengan panjang 6 cm, tinggi segitiga 4 cm, dan tinggi limas 10 cm. Hitunglah volume limas segitiga tersebut.
Solusi:
Luas alas = 1/2 x alas x tinggi
Luas alas = 1/2 x 6 x 4
Luas alas = 12 cm^2
V = 1/3 x Luas alas x Tinggi
V = 1/3 x 12 x 10
V = 40 cm^3
Jadi, volume limas segitiga tersebut adalah 40 cm^3.
VI. Kerucut
Kerucut adalah bangun ruang yang memiliki lingkaran sebagai alas dan sebuah selimut yang menutupi lingkaran tersebut. Volume kerucut dapat dihitung dengan menggunakan rumus:
V = 1/3πr^2t
dimana V adalah volume, π adalah nilai pi (3.14), r adalah jari-jari kerucut, dan t adalah tinggi ker
 Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
