Daftar Isi
Pendahuluan
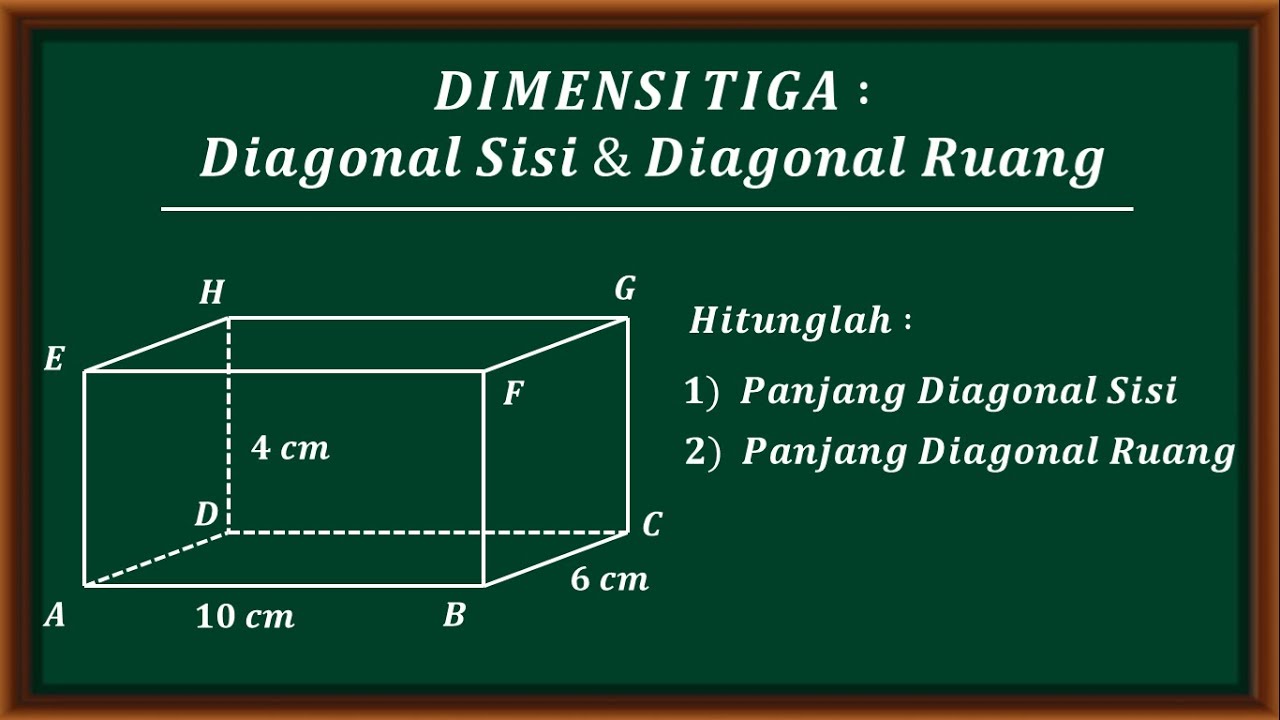
Balok adalah bangun ruang tiga dimensi yang sering kita jumpai dalam kehidupan sehari-hari. Dalam matematika, rumus panjang diagonal ruang balok sangat penting untuk diketahui karena dapat membantu kita menghitung berbagai macam ukuran yang terkait dengan balok. Diagonal ruang balok adalah garis lurus yang menghubungkan dua titik di sudut balok yang bersebrangan. Pada artikel ini, kita akan membahas rumus panjang diagonal ruang balok beserta langkah-langkahnya.
Rumus Panjang Diagonal Ruang Balok
Rumus panjang diagonal ruang balok dapat dihitung dengan menggunakan teorema Pythagoras. Teorema Pythagoras menyatakan bahwa dalam segitiga siku-siku, kuadrat panjang sisi miring (diagonal ruang dalam hal ini) sama dengan jumlah kuadrat panjang sisi yang lain. Dengan demikian, rumus panjang diagonal ruang balok adalah sebagai berikut:
d = √(p² + l² + t²)
Di mana d adalah panjang diagonal ruang, p adalah panjang balok, l adalah lebar balok, dan t adalah tinggi balok.
Langkah-langkah Menghitung Panjang Diagonal Ruang Balok
Berikut adalah langkah-langkah untuk menghitung panjang diagonal ruang balok:
1. Tentukan nilai p, l, dan t
Sebelum menghitung panjang diagonal ruang balok, kita perlu menentukan nilai dari panjang (p), lebar (l), dan tinggi (t) balok. Nilai-nilai ini dapat diukur menggunakan satuan panjang yang berbeda-beda, seperti meter, sentimeter, atau bahkan inchi.
2. Kuadratkan nilai p, l, dan t
Setelah menentukan nilai p, l, dan t, langkah selanjutnya adalah mengkuadratkan masing-masing nilainya. Ini dilakukan dengan cara mengalikan nilai tersebut dengan dirinya sendiri. Misalnya, jika nilai p adalah 5, maka kita harus mengalikan 5 dengan 5 sehingga didapatkan nilai 25.
3. Jumlahkan nilai p², l², dan t²
Setelah mengkuadratkan nilai p, l, dan t, langkah selanjutnya adalah menjumlahkan ketiga nilai tersebut. Ini dilakukan dengan cara menjumlahkan nilai-nilai yang sudah dikuaradatkan. Misalnya, jika nilai p² adalah 25, nilai l² adalah 16, dan nilai t² adalah 9, maka jumlahkan ketiga nilai tersebut sehingga didapatkan nilai 50.
4. Ambil akar kuadrat dari jumlah nilai p², l², dan t²
Setelah menjumlahkan ketiga nilai yang sudah dikuaradatkan, langkah selanjutnya adalah mengambil akar kuadrat dari jumlah tersebut. Ini dilakukan dengan cara mengambil akar kuadrat dari nilai yang sudah dijumlahkan pada langkah sebelumnya. Misalnya, jika jumlah nilai p², l², dan t² adalah 50, maka kita harus mengambil akar kuadrat dari 50 sehingga didapatkan nilai panjang diagonal ruang balok.
Contoh Soal dan Pembahasan
Berikut adalah contoh soal dan pembahasan mengenai rumus panjang diagonal ruang balok:
Contoh soal:
Sebuah balok memiliki panjang 8 cm, lebar 6 cm, dan tinggi 10 cm. Hitunglah panjang diagonal ruang balok tersebut!
Pembahasan:
1. Tentukan nilai p, l, dan t
Panjang balok (p) = 8 cm
Lebar balok (l) = 6 cm
Tinggi balok (t) = 10 cm
2. Kuadratkan nilai p, l, dan t
p² = 8² = 64
l² = 6² = 36
t² = 10² = 100
3. Jumlahkan nilai p², l², dan t²
64 + 36 + 100 = 200
4. Ambil akar kuadrat dari jumlah nilai p², l², dan t²
√200 ≈ 14,14
Jadi, panjang diagonal ruang balok tersebut adalah sekitar 14,14 cm.
Kesimpulan
Dalam artikel ini, kita telah membahas tentang rumus panjang diagonal ruang balok beserta langkah-langkahnya. Rumus panjang diagonal ruang balok sangat berguna dalam menghitung berbagai macam ukuran yang berhubungan dengan balok. Selain itu, rumus ini juga dapat digunakan untuk menghitung panjang diagonal ruang bangun ruang tiga dimensi lainnya, seperti kubus atau prisma. Dengan memahami rumus panjang diagonal ruang balok, kita dapat menyelesaikan berbagai macam soal matematika yang berkaitan dengan balok.
Pencarian Berdasarkan Kata Kunci: cara menghitung diagonal ruang pada balok-
 Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
