Rumus Matematika Kelas 6 Yang Harus Dikuasai: Cara Menghitung Luas Dan Keliling Dengan Mudah

Rumus-Rumus Matematika Kelas 6

Matematika adalah salah satu mata pelajaran yang memerlukan pemahaman yang baik agar bisa memahami materi dan menguasai rumus-rumusnya. Rumus-rumus matematika sangat penting bagi siswa di kelas 6, karena mereka akan mempelajari topik-topik yang lebih rumit seperti pecahan, bilangan bulat, dan aljabar. Oleh karena itu, ini adalah artikel tentang rumus-rumus matematika kelas 6 yang harus dipahami siswa.

1. Rumus Keliling dan Luas Bangun Datar

Bangun datar adalah bentuk geometris yang terdiri dari garis dan titik, dan mereka memiliki luas dan keliling yang dapat dihitung. Berikut adalah rumus-rumus untuk menghitung keliling dan luas beberapa bangun datar:

a. Persegi

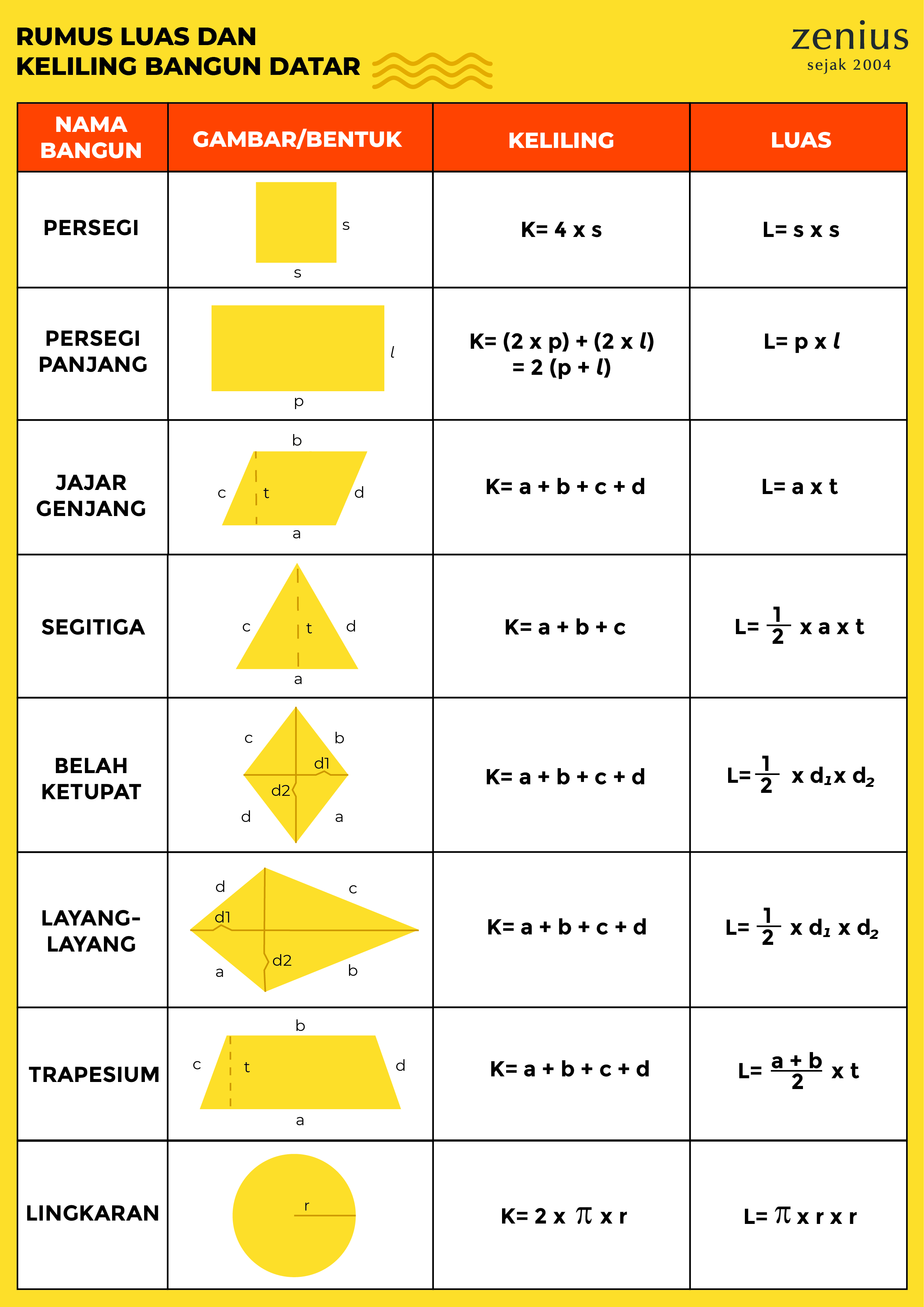
Persegi adalah bangun datar yang memiliki keempat sisi yang sama panjang. Rumus-rumus persegi adalah:

– Keliling persegi = 4 x sisi
– Luas persegi = sisi x sisi

b. Persegi Panjang

Persegi panjang adalah bangun datar yang memiliki dua pasang sisi yang sama panjang dan sudutnya siku-siku. Rumus-rumus persegi panjang adalah:

– Keliling persegi panjang = 2 x (panjang + lebar)
– Luas persegi panjang = panjang x lebar

c. Segitiga

Segitiga adalah bangun datar yang memiliki tiga sisi dan tiga sudut. Rumus-rumus segitiga adalah:

– Keliling segitiga = sisi 1 + sisi 2 + sisi 3
– Luas segitiga = 1/2 x alas x tinggi

d. Jajar Genjang

Jajar genjang adalah bangun datar yang memiliki dua pasang sisi yang sejajar dan sudut-sudut yang sama besar. Rumus-rumus jajar genjang adalah:

– Keliling jajar genjang = 2 x (sisi sejajar 1 + sisi sejajar 2)
– Luas jajar genjang = alas x tinggi

e. Layang-Layang

Layang-layang adalah bangun datar yang memiliki dua pasang sisi yang sejajar dan sudut-sudut yang berbeda besar. Rumus-rumus layang-layang adalah:

– Keliling layang-layang = 2 x (sisi 1 + sisi 2)
– Luas layang-layang = 1/2 x diagonal 1 x diagonal 2

2. Rumus-Rumus Bilangan Bulat

Bilangan bulat adalah angka-angka positif dan negatif, dan mereka memiliki operasi matematika yang berbeda. Berikut adalah rumus-rumus bilangan bulat:

a. Penjumlahan dan Pengurangan Bilangan Bulat

– Bilangan bulat + bilangan bulat = hasil penjumlahan bilangan bulat
– Bilangan bulat – bilangan bulat = hasil pengurangan bilangan bulat

Contoh: 6 + (-3) = 3

b. Perkalian dan Pembagian Bilangan Bulat

– Bilangan bulat x bilangan bulat = hasil perkalian bilangan bulat
– Bilangan bulat / bilangan bulat = hasil pembagian bilangan bulat

Contoh: (-4) x 3 = -12

c. Sifat-Sifat Bilangan Bulat

– Bilangan bulat positif + bilangan bulat positif = bilangan bulat positif
– Bilangan bulat negatif + bilangan bulat negatif = bilangan bulat negatif
– Bilangan bulat positif x bilangan bulat positif = bilangan bulat positif
– Bilangan bulat negatif x bilangan bulat negatif = bilangan bulat positif
– Bilangan bulat positif x bilangan bulat negatif = bilangan bulat negatif

3. Rumus-Rumus Pecahan

Pecahan adalah bentuk bilangan yang terdiri dari pembilang dan penyebut. Mereka memiliki operasi matematika yang berbeda. Berikut adalah rumus-rumus pecahan:

a. Penjumlahan dan Pengurangan Pecahan

– Pecahan + pecahan = hasil penjumlahan pecahan
– Pecahan – pecahan = hasil pengurangan pecahan

Contoh: 1/4 + 3/4 = 1

b. Perkalian dan Pembagian Pecahan

– Pecahan x pecahan = hasil perkalian pecahan
– Pecahan / pecahan = hasil pembagian pecahan

Contoh: 1/2 x 2 = 1

c. Sifat-Sifat Pecahan

– Pecahan sama dengan pecahan yang memiliki pembilang dan penyebut yang sama jika dikurangi atau ditambahkan dengan pecahan lain yang memiliki pembilang dan penyebut yang sama.
– Pecahan dapat disederhanakan dengan membagi pembilang dan penyebut dengan faktor yang sama.

4. Rumus-Rumus Aljabar

Aljabar adalah cabang matematika yang menggunakan huruf-huruf sebagai pengganti bilangan. Berikut adalah rumus-rumus aljabar:

a. Persamaan Aljabar

Persamaan aljabar adalah persamaan yang menggunakan huruf-huruf sebagai pengganti bilangan. Contoh:

2x + 3 = 9

Dalam contoh di atas, x adalah huruf yang digunakan sebagai pengganti bilangan. Untuk menyelesaikan persamaan tersebut, kita harus mencari nilai x yang membuat persamaan tersebut benar.

b. Suku Aljabar

Suku aljabar adalah bagian-bagian dalam persamaan aljabar yang dipisahkan oleh tanda tambah atau tanda kurang. Contoh:

2x + 3 = 9

Dalam contoh di atas, 2x dan 3 adalah suku aljabar.

c. Koefisien Aljabar

Koefisien aljabar adalah bilangan yang digunakan untuk mengalikan suku aljabar. Contoh:

2x + 3 = 9

Dalam contoh di atas, koefisien untuk suku 2x adalah 2.

d. Variabel

Variabel adalah huruf yang digunakan sebagai pengganti bilangan dalam persamaan aljabar. Contoh:

2x + 3 = 9

Dalam contoh di atas, x adalah variabel.

e. Kaidah-Kaidah Aljabar

– Untuk menyelesaikan persamaan aljabar, kita harus menyelesaikan suku-suku aljabar yang sama terlebih dahulu.
– Untuk menyelesaikan persamaan aljabar, kita harus menghilangkan koefisien terlebih dahulu dengan membagi kedua sisi persamaan dengan koefisien tersebut.
– Untuk menyelesaikan persamaan aljabar, kita harus memindahkan variabel ke satu sisi persamaan dan bilangan ke sisi yang lain.

5. Rumus-Rumus Statistika

Statistika adalah cabang matematika yang mempelajari cara mengumpulkan, menganalisis, dan menginterpretasi data. Berikut adalah rumus-rumus statistika:

a. Mean

Mean adalah nilai rata-rata dari suatu set data. Rumus mean adalah:

Mean = (jumlah semua data) / (jumlah data)

Contoh: Jika kita memiliki data 1, 2, 3, 4, dan 5, maka mean dari data tersebut adalah:

Mean = (1 + 2 + 3 + 4 + 5) / 5 = 3

b. Median

Median adalah nilai tengah dari suatu set data. Rumus median adalah:

– Jika jumlah data ganjil: median = data yang berada di tengah
– Jika jumlah data genap: median = (data ke-(n/2) + data ke-(n/2+1)) / 2

Contoh: Jika kita memiliki data 1, 2, 3, 4, dan 5, maka median dari data tersebut adalah:

Median = 3

c. Modus

Modus adalah nilai yang paling sering muncul dalam suatu set data. Contoh: Jika kita memiliki data 1, 2,