Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Daftar Isi
Rumus Siku Siku adalah rumus matematika yang berguna untuk mencari sisi miring segitiga siku-siku. Segitiga siku-siku adalah segitiga yang salah satu sudutnya adalah sudut 90 derajat. Dalam segitiga siku-siku, sisi yang bersebrangan dengan sudut 90 derajat disebut sebagai sisi miring. Rumus Siku Siku adalah rumus yang paling dasar dan sering digunakan dalam matematika.
Penjelasan Rumus Siku Siku
Rumus Siku Siku digunakan untuk menghitung panjang sisi miring dari segitiga siku-siku. Rumus ini juga dikenal sebagai Teorema Pythagoras. Teorema Pythagoras menyatakan bahwa kuadrat dari sisi miring (c) sama dengan jumlah kuadrat dari kedua sisi lainnya (a dan b).
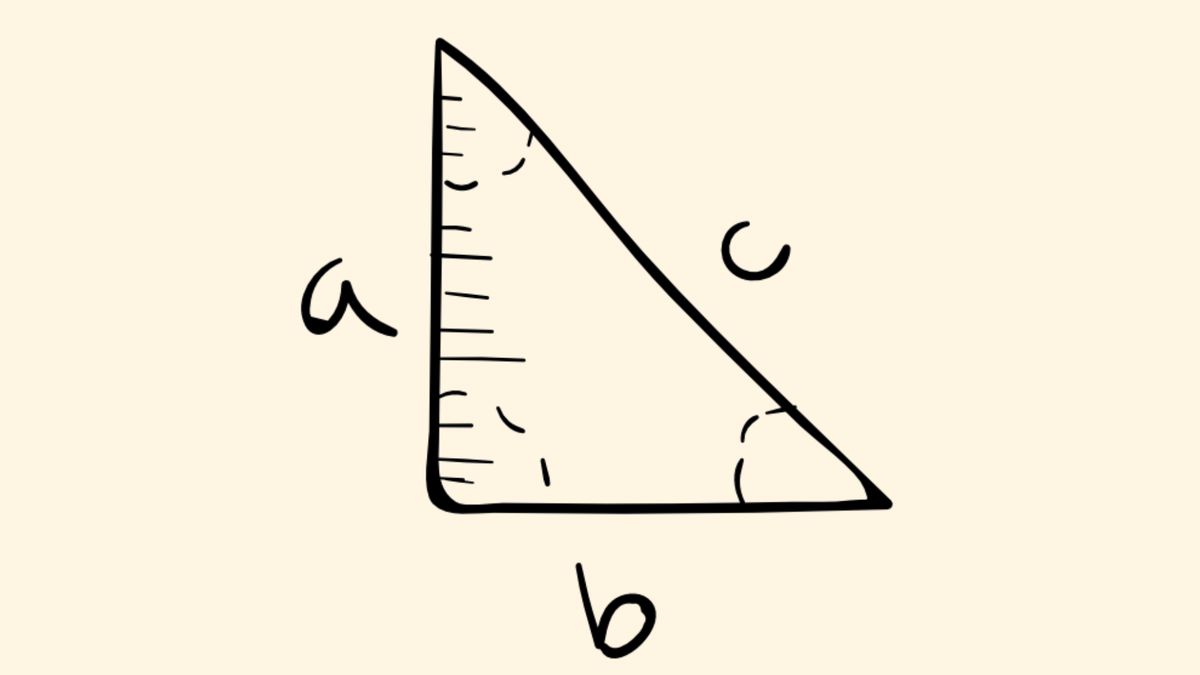
Rumus Siku Siku dapat ditulis dalam bentuk matematika sebagai berikut:
c^2 = a^2 + b^2
Di mana:
c adalah sisi miring segitiga siku-siku
a dan b adalah sisi-sisi lain dari segitiga siku-siku
Dalam rumus ini, sisi miring segitiga siku-siku dinyatakan sebagai kuadrat dari sisi-sisi lainnya. Oleh karena itu, untuk mencari panjang sisi miring, kita perlu menghitung akar kuadrat dari jumlah kuadrat sisi-sisi lainnya.
Langkah-langkah Menggunakan Rumus Siku Siku
Berikut adalah langkah-langkah untuk menggunakan Rumus Siku Siku:
1. Tentukan sisi mana yang merupakan sisi miring segitiga siku-siku.
2. Identifikasi sisi-sisi yang lain dari segitiga siku-siku.
3. Kuadratkan panjang kedua sisi tersebut.
4. Jumlahkan kedua hasil kuadrat tersebut.
5. Ambil akar kuadrat dari hasil penjumlahan tersebut.
6. Hasil akar kuadrat tersebut adalah panjang sisi miring segitiga siku-siku.
Contoh Soal Rumus Siku Siku
Berikut adalah contoh soal yang dapat diselesaikan menggunakan Rumus Siku Siku:
Contoh 1:
Sebuah segitiga siku-siku memiliki sisi-sisi a = 3 cm dan b = 4 cm. Tentukan panjang sisi miring c.
Penyelesaian:
Langkah 1:
Sisi miring segitiga siku-siku adalah c.
Langkah 2:
Sisi-sisi lain dari segitiga siku-siku adalah a = 3 cm dan b = 4 cm.
Langkah 3:
Kuadratkan kedua sisi tersebut:
a^2 = 3^2 = 9
b^2 = 4^2 = 16
Langkah 4:
Tambahkan kedua hasil kuadrat tersebut:
9 + 16 = 25
Langkah 5:
Ambil akar kuadrat dari hasil penjumlahan tersebut:
√25 = 5
Langkah 6:
Hasil akar kuadrat tersebut adalah panjang sisi miring segitiga siku-siku:
c = 5 cm
Jadi, panjang sisi miring dari segitiga siku-siku dengan sisi a = 3 cm dan b = 4 cm adalah 5 cm.
Contoh 2:
Sebuah kawat berbentuk segitiga siku-siku memiliki sisi-sisi a = 6 cm dan c = 10 cm. Tentukan panjang sisi b.
Penyelesaian:
Langkah 1:
Sisi miring segitiga siku-siku adalah c.
Langkah 2:
Sisi-sisi lain dari segitiga siku-siku adalah a = 6 cm dan b.
Langkah 3:
Kuadratkan sisi a:
a^2 = 6^2 = 36
Langkah 4:
Kuadratkan sisi c:
c^2 = 10^2 = 100
Langkah 5:
Kurangi kuadrat sisi a dari kuadrat sisi c:
c^2 – a^2 = 100 – 36 = 64
Langkah 6:
Ambil akar kuadrat dari selisih tersebut:
√64 = 8
Langkah 7:
Hasil akar kuadrat tersebut adalah panjang sisi b:
b = 8 cm
Jadi, panjang sisi b dari segitiga siku-siku dengan sisi a = 6 cm dan c = 10 cm adalah 8 cm.
Kesimpulan
Rumus Siku Siku adalah rumus matematika paling dasar dan sering digunakan dalam segitiga siku-siku. Rumus ini juga dikenal sebagai Teorema Pythagoras. Rumus Siku Siku menghitung panjang sisi miring segitiga siku-siku dengan cara menghitung akar kuadrat dari jumlah kuadrat sisi-sisi lainnya. Untuk menggunakan rumus ini, sisi mana yang merupakan sisi miring harus ditentukan terlebih dahulu. Setelah itu, langkah-langkahnya adalah mengidentifikasi sisi-sisi lain dari segitiga siku-siku, mengkuadratkan kedua sisi tersebut, menambahkan kedua hasil kuadrat tersebut, mengambil akar kuadrat dari hasil penjumlahan, dan menghasilkan panjang sisi miring. Dengan memahami Rumus Siku Siku, kita dapat menyelesaikan berbagai macam masalah matematika yang melibatkan segitiga siku-siku.
