Daftar Isi
Pengertian Barisan Dan Deret
Barisan dan deret adalah konsep matematika yang umum digunakan dalam berbagai aplikasi, mulai dari ilmu ekonomi, teknik, hingga statistik. Keduanya sering disebut sebagai suatu rangkaian bilangan yang memiliki pola tertentu.
Barisan adalah kumpulan bilangan yang disusun secara berurutan. Setiap bilangan dalam barisan memiliki urutan yang jelas dan dapat dicatat menggunakan notasi khusus, seperti a1, a2, a3, dan seterusnya. Barisan juga dapat memiliki pola tertentu, seperti penambahan, pengurangan, atau perkalian dengan suatu bilangan konstan.
Sedangkan deret adalah hasil penjumlahan dari bilangan-bilangan dalam sebuah barisan. Notasi untuk deret biasanya ditulis sebagai S, diikuti dengan subskrip untuk membantu mengidentifikasi barisan yang akan dijumlahkan, seperti S1, S2, S3, dan seterusnya. Deret dapat berupa deret aritmatika atau geometri, tergantung pada pola bilangan yang ada dalam barisan.
Barisan Aritmatika
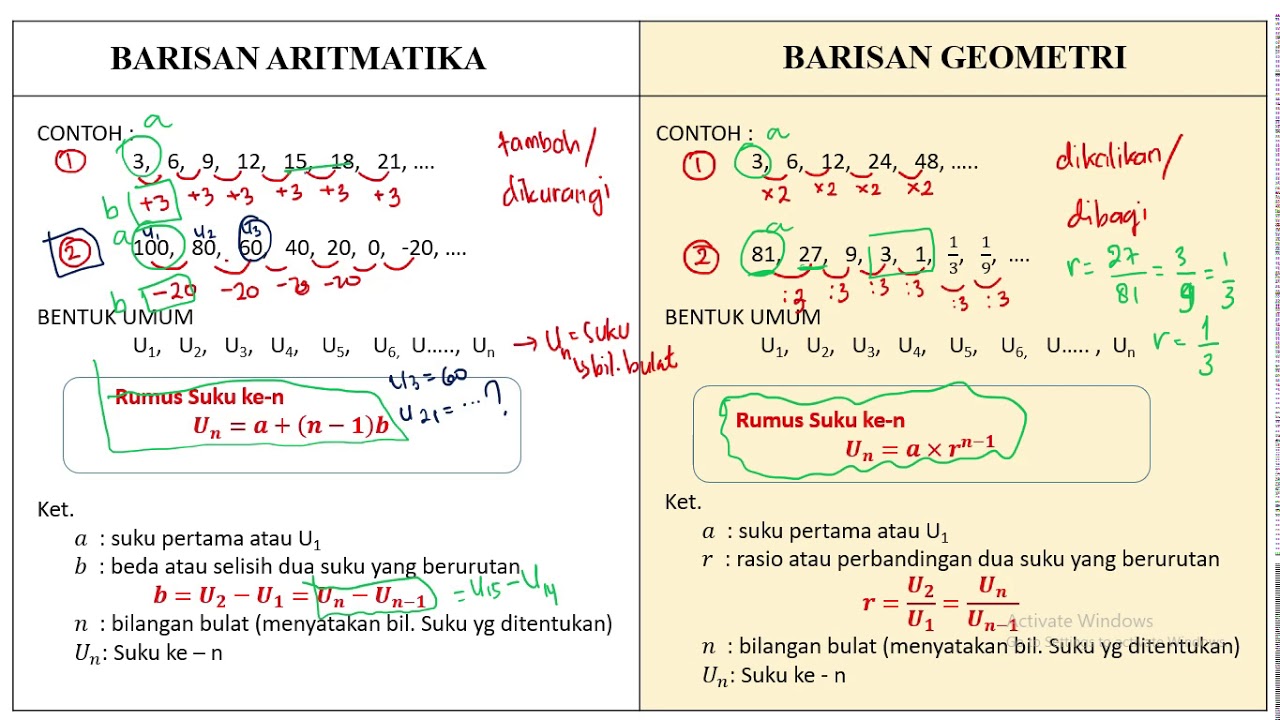
Barisan aritmatika adalah barisan bilangan dengan pola penambahan atau pengurangan yang sama antara setiap dua bilangan berturut-turut. Dalam barisan aritmatika, setiap bilangan diperoleh dengan menambahkan atau mengurangi bilangan sebelumnya dengan bilangan tetap yang disebut sebagai beda atau selisih. Notasi umum untuk barisan aritmatika adalah sebagai berikut:
a1, a1 + d, a1 + 2d, a1 + 3d, …, a1 + (n-1)d
Dalam notasi tersebut, a1 merupakan suku pertama atau elemen awal dari barisan, d merupakan beda atau selisih antara setiap dua bilangan berturut-turut, dan n merupakan jumlah suku dalam barisan.
Contoh soal:
Diberikan barisan aritmatika dengan suku pertama 3 dan beda 4. Tentukan suku ke-10 dari barisan tersebut.
Penyelesaian:
a1 = 3
d = 4
n = 10
Rumus untuk mencari suku ke-n dari barisan aritmatika adalah sebagai berikut:
an = a1 + (n-1)d
Maka, suku ke-10 dari barisan aritmatika tersebut adalah:
a10 = a1 + (10-1)d
a10 = 3 + (10-1)4
a10 = 3 + 36
a10 = 39
Sehingga, suku ke-10 dari barisan aritmatika dengan suku pertama 3 dan beda 4 adalah 39.
Barisan Geometri
Barisan geometri adalah barisan bilangan dengan pola perkalian yang sama antara setiap dua bilangan berturut-turut. Dalam barisan geometri, setiap bilangan diperoleh dengan mengalikan bilangan sebelumnya dengan bilangan tetap yang disebut sebagai rasio atau rasio geometri. Notasi umum untuk barisan geometri adalah sebagai berikut:
a1, a1r, a1r^2, a1r^3, …, a1r^(n-1)
Dalam notasi tersebut, a1 merupakan suku pertama atau elemen awal dari barisan, r merupakan rasio atau rasio geometri antara setiap dua bilangan berturut-turut, dan n merupakan jumlah suku dalam barisan.
Contoh soal:
Diberikan barisan geometri dengan suku pertama 2 dan rasio 3/2. Tentukan suku ke-7 dari barisan tersebut.
Penyelesaian:
a1 = 2
r = 3/2
n = 7
Rumus untuk mencari suku ke-n dari barisan geometri adalah sebagai berikut:
an = a1 * r^(n-1)
Maka, suku ke-7 dari barisan geometri tersebut adalah:
a7 = a1 * r^(7-1)
a7 = 2 * (3/2)^(7-1)
a7 = 2 * (3/2)^6
a7 = 2 * 81/64
a7 = 162/64
a7 = 2.53125
Sehingga, suku ke-7 dari barisan geometri dengan suku pertama 2 dan rasio 3/2 adalah 2.53125.
Deret Aritmatika
Deret aritmatika adalah hasil penjumlahan dari bilangan-bilangan dalam sebuah barisan aritmatika. Notasi umum untuk deret aritmatika adalah sebagai berikut:
S = a1 + a2 + a3 + … + an-1 + an
Dalam notasi tersebut, a1 merupakan suku pertama atau elemen awal dari barisan aritmatika, an merupakan suku ke-n atau elemen terakhir dari barisan aritmatika, dan n merupakan jumlah suku dalam barisan.
Rumus umum untuk mencari jumlah suku-suku dalam deret aritmatika adalah sebagai berikut:
S = (n/2) * (a1 + an)
Contoh soal:
Diberikan deret aritmatika dengan suku pertama 5, suku terakhir 41, dan jumlah suku 8. Tentukan jumlah deret tersebut.
Penyelesaian:
a1 = 5
an = 41
n = 8
Rumus untuk mencari jumlah suku-suku dalam deret aritmatika adalah sebagai berikut:
S = (n/2) * (a1 + an)
Maka, jumlah deret aritmatika tersebut adalah:
S = (8/2) * (5 + 41)
S = 4 * 46
S = 184
Sehingga, jumlah deret aritmatika dengan suku pertama 5, suku terakhir 41, dan jumlah suku 8 adalah 184.
Deret Geometri
Deret geometri adalah hasil penjumlahan dari bilangan-bilangan dalam sebuah barisan geometri. Notasi umum untuk deret geometri adalah sebagai berikut:
S = a1 + a1r + a1r^2 + … + a1r^n-2 + a1r^n-1
Dalam notasi tersebut, a1 merupakan suku pertama atau elemen awal dari barisan geometri, r merupakan rasio atau rasio geometri antara setiap dua bilangan berturut-turut, dan n merupakan jumlah suku dalam barisan.
Rumus umum untuk mencari jumlah suku-suku dalam deret geometri adalah sebagai berikut:
S = (a1 * (1-r^n)) / (1-r)
Contoh soal:
Diberikan deret geometri dengan suku pertama 2 dan rasio 3/2. Tentukan jumlah deret tersebut jika terdapat 6 suku dalam deret tersebut.
Penyelesaian:
a1 = 2
r = 3/2
n = 6
Rumus untuk mencari jumlah suku-suku dalam deret geometri adalah sebagai berikut:
S = (a1 * (1-r^n)) / (1-r)
Maka, jumlah deret geometri tersebut adalah:
S = (2 * (1-(3/2)^6)) / (1-(3/2))
S = (2 * (1-729/64)) / (-1/2)
S = (2 * (-665/64)) / (-1/2)
S = 1330/32
S = 41.875
Sehingga, jumlah deret geometri dengan suku pertama 2 dan rasio 3/2 jika terdapat 6 suku dalam deret tersebut adalah 41.875.
Kesimpulan
Barisan dan deret merupakan konsep matematika yang sangat penting dalam berbagai aplikasi di dunia nyata. Barisan aritmatika dan geometri memiliki pola tertentu yang memudahkan dalam mencari suku-suku dalam barisan atau jumlah suku-suku dalam deret. Masing-masing barisan dan deret memiliki rumus umum yang dapat digunakan untuk menyelesaikan berbagai macam permasalahan. Dengan memahami konsep barisan dan deret, kita dapat menggunakan matematika dengan lebih efektif dan efisien dalam kehidupan sehari-hari.
 Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
