Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Daftar Isi
Pengenalan
Teorema Pythagoras adalah salah satu konsep matematika dasar dalam geometri yang dapat diterapkan pada segitiga siku-siku. Rumus ini digunakan untuk menemukan panjang sisi miring (hipotenusa) sebuah segitiga siku-siku jika diketahui panjang kedua sisi lainnya, yaitu sisi pendek atau kaki yang membentuk sudut siku-siku.
Rumus teorema Pythagoras ditemukan oleh seorang ahli matematika Yunani kuno bernama Pythagoras. Teorema ini menyatakan bahwa kuadrat dari panjang sisi miring sebuah segitiga siku-siku sama dengan jumlah kuadrat dari kedua sisi pendeknya.
Perumusan Teorema Pythagoras
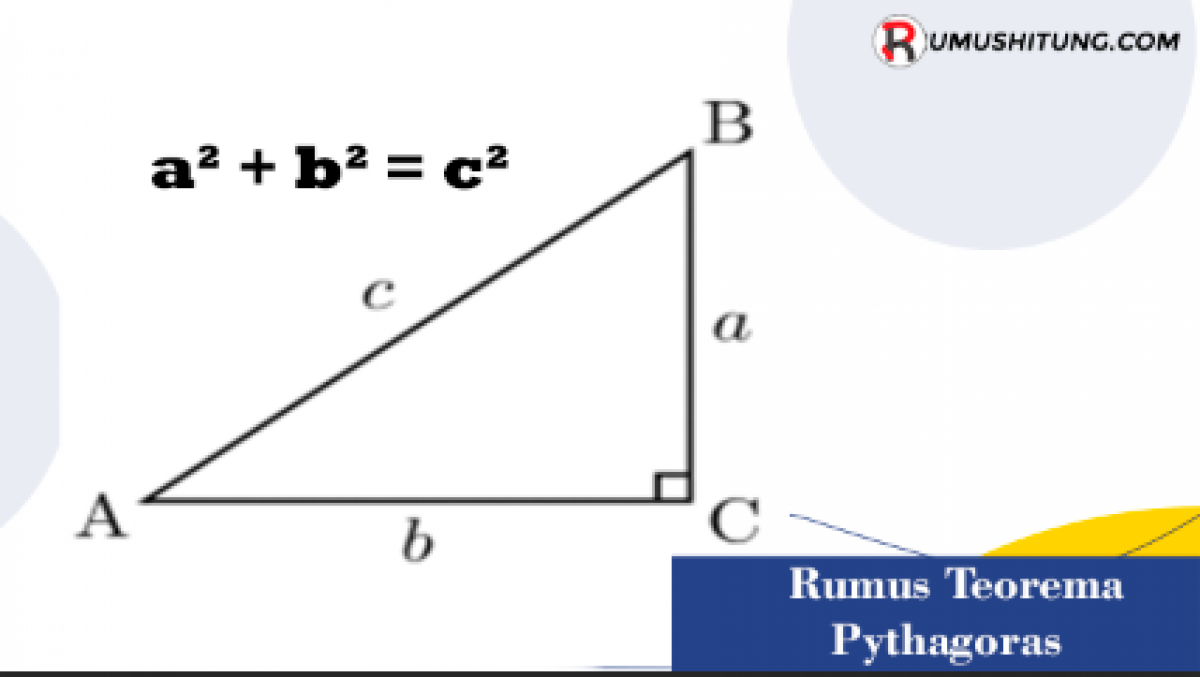
Rumus teorema Pythagoras dapat dirumuskan dalam notasi matematika sebagai berikut:
a^2 + b^2 = c^2
Di mana a dan b adalah panjang kedua sisi pendek atau kaki pada segitiga siku-siku, sedangkan c adalah panjang sisi miring atau hipotenusa.
Contoh Penerapan Rumus Teorema Pythagoras
Berikut adalah contoh penerapan rumus teorema Pythagoras pada sebuah segitiga siku-siku yang memiliki sisi pendek atau kaki sepanjang 3 cm dan 4 cm:
a^2 + b^2 = c^2
3^2 + 4^2 = c^2
9 + 16 = c^2
25 = c^2
c = √25
c = 5
Dari hasil perhitungan tersebut, dapat disimpulkan bahwa panjang sisi miring atau hipotenusa pada segitiga siku-siku tersebut adalah 5 cm.
Langkah-langkah Mencari Panjang Sisi Miring dengan Rumus Teorema Pythagoras
Berikut adalah langkah-langkah untuk mencari panjang sisi miring atau hipotenusa sebuah segitiga siku-siku menggunakan rumus teorema Pythagoras:
Langkah 1: Identifikasi Sisi-sisi Segitiga
Identifikasi sisi-sisi segitiga yang dimaksud, yaitu sisi pendek atau kaki yang membentuk sudut siku-siku dan sisi miring atau hipotenusa yang terletak di seberang sudut siku-siku.
Langkah 2: Tentukan Panjang Sisi-sisi Segitiga
Tentukan panjang sisi-sisi segitiga yang diketahui. Misalnya, jika diketahui panjang kedua sisi pendek, maka nilai a dan b dapat ditentukan.
Langkah 3: Gunakan Rumus Teorema Pythagoras
Gunakan rumus teorema Pythagoras untuk mencari panjang sisi miring atau hipotenusa dengan menggantikan nilai a dan b yang telah diketahui ke dalam rumus tersebut.
Langkah 4: Hitung dan Verefikasi Hasil
Hitung dan verefikasi hasil perhitungan yang telah dilakukan. Jika hasil perhitungan sesuai dengan ekspektasi, artinya rumus teorema Pythagoras telah berhasil digunakan untuk mencari panjang sisi miring atau hipotenusa sebuah segitiga siku-siku.
Contoh Soal
Berikut adalah contoh soal penerapan rumus teorema Pythagoras pada sebuah segitiga siku-siku:
Sebuah segitiga siku-siku memiliki sisi pendek atau kaki sepanjang 6 cm dan 8 cm. Tentukanlah panjang sisi miring atau hipotenusa dari segitiga tersebut.
Penyelesaian
Langkah 1: Identifikasi Sisi-sisi Segitiga
Dalam soal ini, yang dimaksud dengan sisi-sisi segitiga adalah sisi pendek atau kaki sepanjang 6 cm dan 8 cm, serta sisi miring atau hipotenusa yang perlu dicari.
Langkah 2: Tentukan Panjang Sisi-sisi Segitiga
Diketahui panjang kedua sisi pendek atau kaki, yaitu a = 6 dan b = 8.
Langkah 3: Gunakan Rumus Teorema Pythagoras
Gunakan rumus teorema Pythagoras untuk mencari panjang sisi miring atau hipotenusa, dengan menggantikan nilai a dan b ke dalam rumus tersebut:
a^2 + b^2 = c^2
6^2 + 8^2 = c^2
36 + 64 = c^2
100 = c^2
c = √100
c = 10
Dari hasil perhitungan tersebut, dapat disimpulkan bahwa panjang sisi miring atau hipotenusa pada segitiga siku-siku tersebut adalah 10 cm.
Langkah 4: Hitung dan Verefikasi Hasil
Hitung dan verifikasi hasil perhitungan yang telah dilakukan. Jika hasil perhitungan sesuai dengan ekspektasi, artinya rumus teorema Pythagoras telah berhasil digunakan untuk mencari panjang sisi miring atau hipotenusa sebuah segitiga siku-siku.
Kesimpulan
Rumus teorema Pythagoras adalah konsep matematika dasar dalam geometri yang dapat digunakan untuk menentukan panjang sisi miring atau hipotenusa sebuah segitiga siku-siku jika diketahui panjang kedua sisi pendek atau kaki yang membentuk sudut siku-siku. Penyelesaian rumus teorema Pythagoras memerlukan empat langkah dasar, yaitu mengidentifikasi sisi-sisi segitiga, menentukan panjang sisi-sisi segitiga, menggunakan rumus teorema Pythagoras, serta menghitung dan verifikasi hasil perhitungan. Dengan memahami konsep teorema Pythagoras dan penerapannya dalam segitiga siku-siku, kita dapat menyelesaikan berbagai permasalahan matematika dengan lebih mudah dan efektif.
