Rumus Matriks Invers: Cara Mudah Membuat Invers Matriks Dengan Exact Keyword

Pengenalan Matriks Invers

Matriks invers merupakan konsep yang sangat penting dalam aljabar linier. Matriks invers adalah matriks yang jika dikalikan dengan matriks asalnya akan menghasilkan matriks identitas.

Contoh: Jika A adalah sebuah matriks dan A-1 adalah matriks inversnya, maka A x A-1 = I, dimana I adalah matriks identitas.

Pada artikel ini, kita akan membahas tentang rumus matriks invers, bagaimana cara menghitungnya, serta contoh penerapannya.

Cara Menghitung Matriks Invers

Sebelum kita masuk ke rumus matriks invers, ada beberapa syarat yang harus terpenuhi agar sebuah matriks memiliki invers.

Syarat Matriks Invers

1. Determinan matriks harus tidak sama dengan nol (det(A) ≠ 0)
2. Matriks harus merupakan matriks persegi (n x n)

Jika kedua syarat tersebut terpenuhi, maka matriks tersebut memiliki invers.

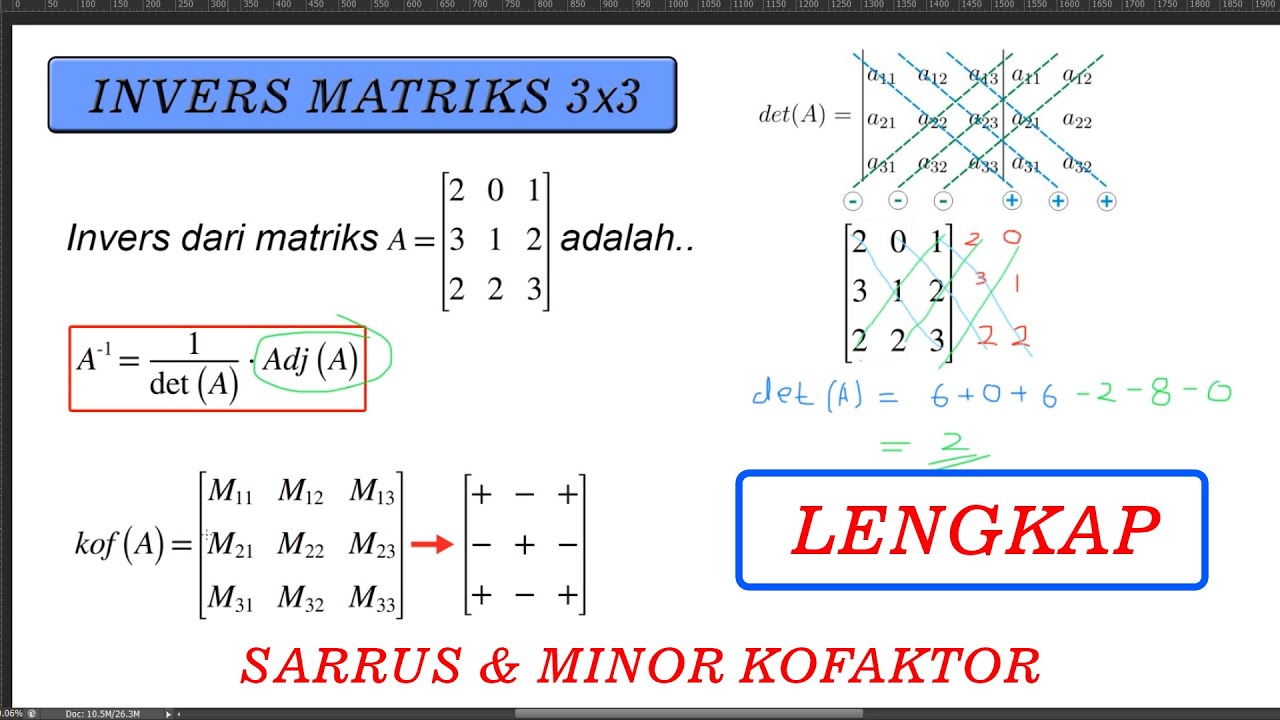
Rumus Matriks Invers

Rumus matriks invers adalah sebagai berikut:

A-1 = (1/det(A)) x (adj(A))

dimana det(A) adalah determinan dari matriks A, dan adj(A) adalah matriks adjoint dari matriks A.

Pengertian Determinan

Determinan adalah nilai skalar yang dihasilkan dari sebuah matriks. Determinan matriks persegi A dinyatakan dengan det(A).

Rumus untuk menghitung determinan matriks A adalah sebagai berikut:

det(A) = a11C11 + a12C12 + … + (-1)n+1a1nC1n

dimana aij adalah elemen pada baris i dan kolom j dari matriks A, Cij adalah kofaktor dari elemen aij, dan n adalah ukuran matriks A.

Kofaktor Cij didefinisikan sebagai (-1)i+j x det(Aij), dimana Aij adalah matriks minor dari matriks A yang dihasilkan dengan menghapus baris i dan kolom j.

Pengertian Matriks Adjoint

Matriks adjoint atau matriks adjoin dari sebuah matriks A, yang dinyatakan dengan adj(A), adalah matriks transpose dari matriks kofaktor A yang dibentuk dengan mengubah tanda dari elemen yang berada pada posisi ganjil.

Contoh: Misalkan A adalah sebuah matriks 3×3, maka matriks adjoint dari A adalah sebagai berikut:

adj(A) = [C11 C21 C31; C12 C22 C32; C13 C23 C33]T

dimana Cij adalah kofaktor dari elemen aij pada matriks A.

Contoh Menghitung Matriks Invers

Misalkan kita memiliki matriks A berikut:

A = [3 2 1; 0 1 4; 2 3 2]

Untuk menghitung matriks invers dari A, kita perlu menghitung determinan A dan matriks adjoint A.

Menghitung Determinan A

det(A) = 3 x det([1 4; 3 2]) – 2 x det([0 4; 2 2]) + 1 x det([0 1; 2 3])
= 3 x (-10) – 2 x (-8) + 1 x (-2)
= -30

Menghitung Matriks Adjoint A

C11 = det([1 4; 3 2]) = -10
C12 = -1 x det([0 4; 2 2]) = 8
C13 = det([0 1; 2 3]) = -2
C21 = -1 x det([2 1; 3 2]) = -1
C22 = det([3 1; 2 2]) = 5
C23 = -1 x det([3 2; 2 3]) = -1
C31 = det([2 1; 1 4]) = 7
C32 = -1 x det([3 1; 0 4]) = 12
C33 = det([3 2; 0 1]) = 3

Sehingga,

adj(A) = [-10 1 7; 8 5 -1; -2 -1 3]

Menghitung Matriks Invers A

A-1 = (1/det(A)) x (adj(A))
= (-1/30) x [-10 1 7; 8 5 -1; -2 -1 3] = [5/3 -1/10 -7/30; -4/15 -1/6 1/15; 1/15 1/30 -1/10]

Maka matriks invers dari A adalah:

A-1 = [5/3 -1/10 -7/30; -4/15 -1/6 1/15; 1/15 1/30 -1/10]

Penerapan Matriks Invers

Salah satu penerapan matriks invers adalah dalam menghitung sistem persamaan linear. Dalam sistem persamaan linear, kita dituntut untuk mencari nilai dari beberapa variabel (x1, x2, …, xn) yang memenuhi beberapa persamaan linear.

Contoh:

3×1 + 2×2 – x3 = 7
x1 + x2 + 4×3 = 4
2×1 + 3×2 + 2×3 = 10

Persamaan-persamaan di atas dapat dituliskan dalam bentuk matriks:

[3 2 -1; 1 1 4; 2 3 2] [x1; x2; x3] = [7; 4; 10]

Jika kita ingin mencari nilai dari variabel x1, x2, dan x3, maka kita bisa menggunakan matriks invers A-1 dari matriks A dan mengalikan kedua sisi persamaan dengan A-1.

A-1 [3 2 -1; 1 1 4; 2 3 2] [x1; x2; x3] = A-1 [7; 4; 10]

I [x1; x2; x3] = A-1 [7; 4; 10]

Dari sini, kita bisa menghitung nilai dari variabel x1, x2, dan x3.

[x1; x2; x3] = A-1 [7; 4; 10]

Contoh perhitungan:

A = [3 2 -1; 1 1 4; 2 3 2]

det(A) = 3 x det([1 4; 3 2]) – 2 x det([