Rumus Luas Bangun Ruang

Bangun ruang adalah benda geometri yang memiliki tiga dimensi, yaitu panjang, lebar, dan tinggi. Dalam matematika, kita sering menghitung luas bangun ruang untuk menentukan berapa banyak ruang yang dapat ditempati oleh benda tersebut. Rumus luas bangun ruang adalah cara untuk menghitung luas permukaan dari bangun ruang.

Rumus luas bangun ruang sangat penting dalam matematika karena dapat digunakan untuk menyelesaikan berbagai masalah yang berhubungan dengan bangun ruang. Rumus ini juga berguna dalam kehidupan sehari-hari, seperti dalam perancangan bangunan, pembuatan perabotan rumah tangga, dan perhitungan volume bahan kimia dalam laboratorium.

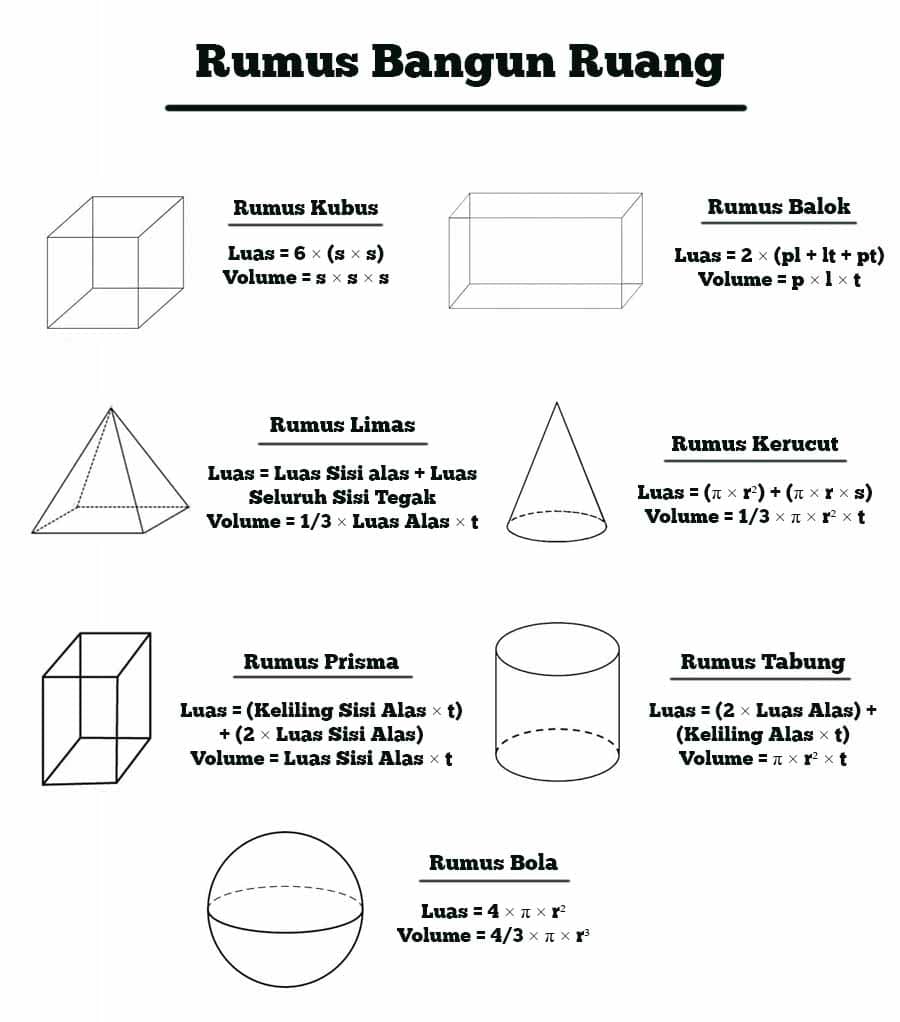
Berikut ini adalah rumus luas bangun ruang yang paling umum digunakan:

1. Luas Permukaan Kubus

Kubus adalah bangun ruang yang memiliki enam sisi yang sama panjang dan sama lebar. Luas permukaan kubus dapat dihitung dengan rumus berikut:

LP = 6 x s x s

Keterangan:
LP = Luas permukaan
s = Sisi kubus

Contoh soal:
Sebuah kubus memiliki sisi 7 cm. Berapa luas permukaan kubus tersebut?

Penyelesaian:
LP = 6 x s x s
LP = 6 x 7 x 7
LP = 294 cm²

Jadi, luas permukaan kubus tersebut adalah 294 cm².

2. Luas Permukaan Balok

Balok adalah bangun ruang yang memiliki dua pasang sisi yang sama panjang dan lebar serta satu pasang sisi yang sama panjang dan lebar. Luas permukaan balok dapat dihitung dengan rumus berikut:

LP = 2 x (pl + lt + pt)

Keterangan:
LP = Luas permukaan
p = Panjang balok
l = Lebar balok
t = Tinggi balok

Contoh soal:
Sebuah balok memiliki panjang 10 cm, lebar 5 cm, dan tinggi 8 cm. Berapa luas permukaan balok tersebut?

Penyelesaian:
LP = 2 x (pl + lt + pt)
LP = 2 x (10 x 5 + 5 x 8 + 8 x 10)
LP = 2 x (50 + 40 + 80)
LP = 2 x 170
LP = 340 cm²

Jadi, luas permukaan balok tersebut adalah 340 cm².

3. Luas Permukaan Prisma Segitiga

Prisma segitiga adalah bangun ruang yang memiliki alas berbentuk segitiga dan dua buah sisi berbentuk segitiga yang sama besar. Luas permukaan prisma segitiga dapat dihitung dengan rumus berikut:

LP = 2 x Ls + Lb

Keterangan:
LP = Luas permukaan
Ls = Luas sisi
Lb = Luas alas

Untuk menghitung luas sisi, dapat menggunakan rumus berikut:

Ls = t x L / 2

Keterangan:
t = Tinggi segitiga
L = Panjang alas segitiga

Contoh soal:
Sebuah prisma segitiga memiliki alas segitiga dengan panjang 10 cm dan tinggi 6 cm serta tinggi prisma 8 cm. Berapa luas permukaan prisma segitiga tersebut?

Penyelesaian:
Ls = t x L / 2
Ls = 6 x 10 / 2
Ls = 30 cm²

Lb = L x t / 2
Lb = 10 x 6 / 2
Lb = 30 cm²

LP = 2 x Ls + Lb
LP = 2 x 30 + 30
LP = 90 cm²

Jadi, luas permukaan prisma segitiga tersebut adalah 90 cm².

4. Luas Permukaan Limas Segitiga

Limas segitiga adalah bangun ruang yang memiliki alas berbentuk segitiga dan tiga buah sisi berbentuk segitiga yang sama besar. Luas permukaan limas segitiga dapat dihitung dengan rumus berikut:

LP = Ls + Lb

Keterangan:
LP = Luas permukaan
Ls = Luas sisi
Lb = Luas alas

Untuk menghitung luas sisi, dapat menggunakan rumus berikut:

Ls = t x L / 2

Keterangan:
t = Tinggi segitiga
L = Panjang alas segitiga

Contoh soal:
Sebuah limas segitiga memiliki alas segitiga dengan panjang 8 cm dan tinggi 6 cm serta tinggi limas 10 cm. Berapa luas permukaan limas segitiga tersebut?

Penyelesaian:
Ls = t x L / 2
Ls = 6 x 8 / 2
Ls = 24 cm²

Lb = L x t / 2
Lb = 8 x 6 / 2
Lb = 24 cm²

LP = Ls + Lb
LP = 24 + 24
LP = 48 cm²

Jadi, luas permukaan limas segitiga tersebut adalah 48 cm².

5. Luas Permukaan Tabung

Tabung adalah bangun ruang yang memiliki dua buah sisi yang sama besar dan berbentuk lingkaran serta satu buah sisi berbentuk persegi panjang. Luas permukaan tabung dapat dihitung dengan rumus berikut:

LP = 2 x Luas Lingkaran + Luas Persegi Panjang

Keterangan:
LP = Luas permukaan
r = Jari-jari lingkaran
t = Tinggi tabung

Untuk menghitung luas lingkaran, dapat menggunakan rumus berikut:

Luas Lingkaran = π x r²

Contoh soal:
Sebuah tabung memiliki jari-jari 7 cm dan tinggi 10 cm. Berapa luas permukaan tabung tersebut?

Penyelesaian:
Luas Lingkaran = π x r²
Luas Lingkaran = π x 7²
Luas Lingkaran = 154 cm²

Luas Persegi Panjang = 2 x π x r x t
Luas Persegi Panjang = 2 x π x 7 x 10
Luas Persegi Panjang = 440 cm²

LP = 2 x Luas Lingkaran + Luas Persegi Panjang
LP = 2 x 154 + 440
LP = 748 cm²

Jadi, luas permukaan tabung tersebut adalah 748 cm².

6. Luas Permukaan Kerucut

Kerucut adalah bangun ruang yang memiliki satu sisi berbentuk lingkaran dan satu sisi berbentuk segitiga. Luas permukaan kerucut dapat dihitung dengan rumus berikut:

LP = Luas Lingkaran + Luas Selimut

Keterangan:
LP = Luas permukaan
r = Jari-jari lingkaran
s = Garis pelukis
t = Tinggi kerucut

Untuk menghitung luas lingkaran, dapat menggunakan rumus berikut:

Luas Lingkaran = π x r²

Untuk menghitung luas selimut, dapat menggunakan rumus berikut:

Luas Selimut = π x r x s

Keterangan:
s = √(r² + t²)

Contoh soal:
Sebuah kerucut memiliki jari-jari 5 cm dan tinggi 8 cm. Berapa luas permukaan kerucut tersebut?

Penyelesaian:
Luas Lingkaran = π x r²
Luas Lingkaran = π x 5²
Luas Lingkaran = 78.5 cm²

s = √(r² + t²)
s = √(5² + 8²)
s = √(25 + 64)
s = √89
s = 9.4 cm

Luas Selimut = π x r x s
Luas Selimut = π x 5 x 9.4
Luas Selimut = 147.9 cm²

LP = Luas Lingkaran + Luas Selimut
LP = 78.5 + 147.9
LP = 226.4 cm²

Jadi, luas permukaan kerucut tersebut adalah 226.4 cm².