Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Daftar Isi
Pendahuluan
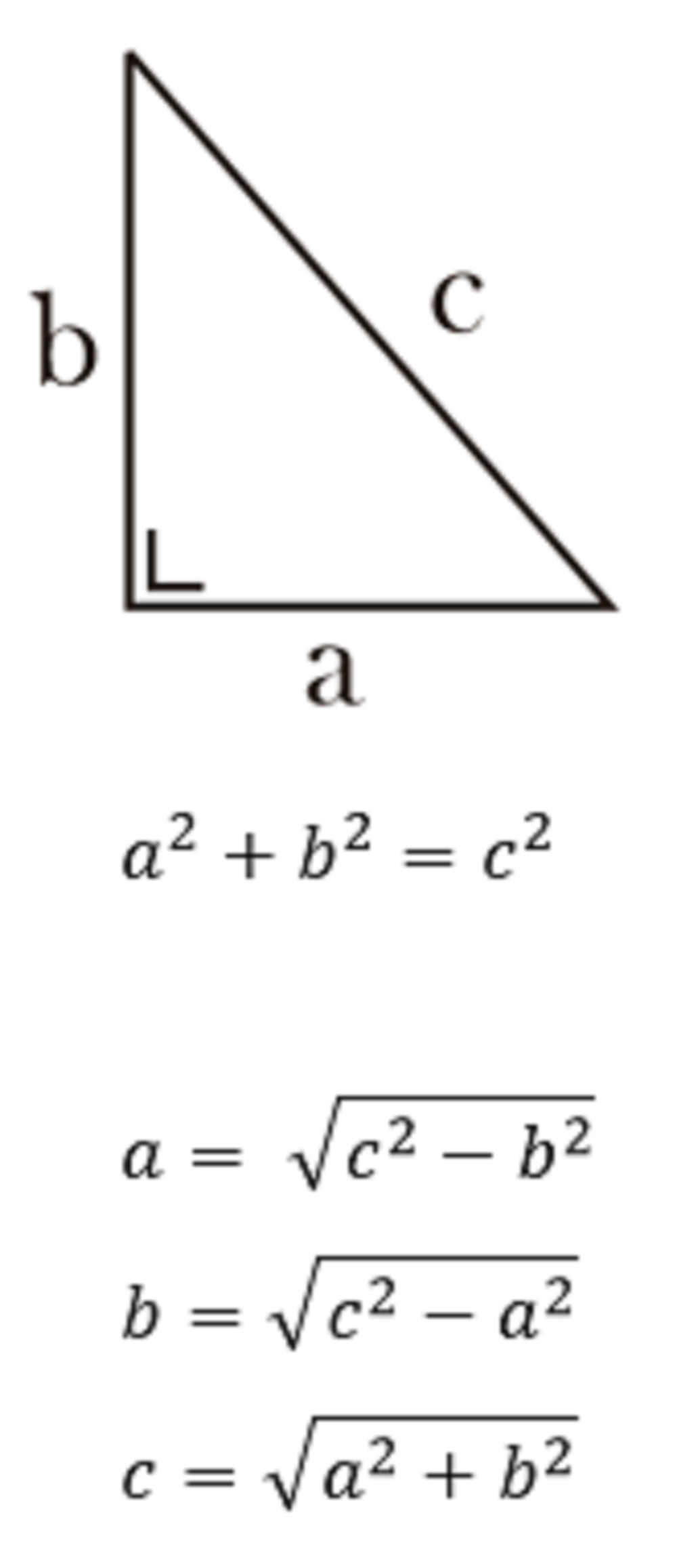
Rumus Teorema Phytagoras adalah salah satu rumus matematika dasar yang dikenal oleh hampir semua orang. Rumus ini ditemukan oleh seorang matematikawan asal Yunani bernama Pythagoras pada abad ke-6 SM. Teorema Phytagoras seringkali digunakan untuk menghitung panjang sisi miring segitiga siku-siku.
Rumus ini sangat penting dalam kehidupan sehari-hari dan sering digunakan dalam berbagai bidang, seperti bangun datar, fisika, dan teknik. Oleh karena itu, penting bagi kita untuk memahami rumus ini dengan baik.
Pada artikel ini, kita akan membahas tentang Rumus Teorema Phytagoras secara lengkap dan detail, dengan langkah-langkah dan contoh soal.
Pengertian Teorema Phytagoras
Teorema Phytagoras menyatakan bahwa dalam segitiga siku-siku, kuadrat dari panjang sisi miring sama dengan jumlah dari kuadrat panjang sisi-sisi yang lain. Rumus matematika dari Teorema Phytagoras dapat dituliskan sebagai berikut:
a² + b² = c²
Di mana a dan b adalah panjang sisi-sisi yang membentuk sudut siku-siku dan c adalah panjang sisi miring yang bersebrangan dengan sudut siku-siku.
Bukti Teorema Phytagoras
Sebelum membahas tentang cara menghitung menggunakan Teorema Phytagoras, kita akan membahas terlebih dahulu tentang bukti Teorema Phytagoras. Bukti ini banyak sekali bermunculan dan telah dikembangkan oleh berbagai orang dari berbagai negara.
Salah satu bukti yang paling dikenal dan mudah dipahami adalah bukti geometris. Bukti ini menggunakan bentuk-bentuk geometris yang berbeda untuk membuktikan Teorema Phytagoras.
Gambar di bawah ini menunjukkan bentuk geometris yang digunakan dalam bukti Teorema Phytagoras.
Bentuk geometris tersebut disebut sebagai kotak Teorema Phytagoras. Dalam kotak tersebut, terdapat empat segitiga yang sama besar dan satu persegi dengan sisi-sisi yang sama panjang.
Kita dapat membuktikan Teorema Phytagoras dengan cara memperbesar benda tersebut seperti pada gambar di bawah ini.
Dalam gambar tersebut, kita dapat melihat bahwa segitiga biru dan segitiga hijau membentuk satu segitiga yang sama besar dengan sudut-sudut yang sama besar. Demikian pula juga dengan segitiga merah dan segitiga hijau.
Kita dapat menghitung luas dari kotak Teorema Phytagoras dengan cara berbeda. Luas kotak tersebut dapat dihitung sebagai berikut:
Luas kotak = luas persegi + 2 x luas segitiga
Lalu, kita dapat mengganti rumus luas segitiga dengan 1/2 x alas x tinggi. Dengan demikian, rumus luas kotak dapat dituliskan sebagai berikut:
Luas kotak = s² + 2 x 1/2 x ab
Luas kotak = s² + ab
Di mana s adalah panjang sisi persegi dan ab adalah luas segitiga.
Kita juga dapat menghitung luas kotak dengan cara lain. Kita dapat menghitung luas kotak sebagai jumlah dari luas keempat segitiga dan luas persegi. Dalam hal ini, rumus luas kotak dapat dituliskan sebagai berikut:
Luas kotak = 4 x 1/2 x ab + s²
Luas kotak = 2ab + s²
Ketika kedua rumus tersebut sama, maka kita dapat menyimpulkan bahwa:
s² + ab = 2ab + s²
ab = c²
Sehingga, kita dapat menyimpulkan bahwa Teorema Phytagoras benar.
Cara Menghitung Menggunakan Teorema Phytagoras
Setelah kita memahami tentang pengertian dan bukti Teorema Phytagoras, kita akan membahas tentang cara menghitung menggunakan Teorema Phytagoras.
Untuk menghitung panjang sisi miring segitiga siku-siku, kita dapat menggunakan rumus berikut:
c = √(a² + b²)
Dalam rumus ini, c adalah panjang sisi miring segitiga siku-siku, a dan b adalah panjang sisi-sisi yang membentuk sudut siku-siku.
Contoh Soal 1:
Sebuah segitiga siku-siku memiliki panjang sisi a sebesar 3 cm dan panjang sisi b sebesar 4 cm. Berapakah panjang sisi miring (c) dari segitiga tersebut?
Penyelesaian:
c = √(a² + b²)
c = √(3² + 4²)
c = √(9 + 16)
c = √25
c = 5
Jadi, panjang sisi miring dari segitiga tersebut adalah 5 cm.
Contoh Soal 2:
Sebuah segitiga siku-siku memiliki panjang sisi a sebesar 5 cm dan panjang sisi miring (c) sebesar 13 cm. Berapakah panjang sisi b dari segitiga tersebut?
Penyelesaian:
c² = a² + b²
b² = c² – a²
b = √(c² – a²)
b = √(13² – 5²)
b = √(169 – 25)
b = √144
b = 12
Jadi, panjang sisi b dari segitiga tersebut adalah 12 cm.
Menentukan Sudut dalam Segitiga Siku-siku Menggunakan Teorema Phytagoras
Selain untuk menghitung panjang sisi miring dalam segitiga siku-siku, Teorema Phytagoras juga dapat digunakan untuk menentukan sudut dalam segitiga siku-siku.
Dalam segitiga siku-siku, sudut yang membentuk sudut siku-siku memiliki besar 90 derajat. Oleh karena itu, kita dapat menggunakan Teorema Phytagoras untuk menentukan besar sudut-sudut dalam segitiga siku-siku.
Contoh Soal 3:
Sebuah segitiga siku-siku memiliki panjang sisi a sebesar 6 cm dan panjang sisi b sebesar 8 cm. Tentukanlah besar sudut C yang merupakan sudut di sebelah sisi miring.
Penyelesaian:
Dalam segitiga siku-siku, sudut C merupakan sudut yang bersebrangan dengan sisi miring.
Cara menentukan sudut C adalah dengan menggunakan rumus tangen.
tangen C = a/b
tangen C = 6/8
tangen C = 0.75
Jadi, untuk menentukan sudut C, kita dapat mencari nilai arctan dari tangen C.
arctan 0.75 = 36.87 derajat
Jadi, besar sudut C pada segitiga siku-siku tersebut adalah 36.87 derajat.
Kesimpulan
Dalam artikel ini, kita telah membahas tentang Rumus Teorema Phytagoras, pengertian Teorema Phytagoras, bukti Teorema Phytagoras, cara menghitung menggunakan Teorema Phytagoras, serta menentukan sudut dalam segitiga siku-siku menggunakan Teorema Phytagoras.
Rumus Teorema Phytagoras adalah salah satu rumus matematika dasar yang sangat penting. Rumus ini sering digunakan dalam kehidupan sehari-hari dan berbagai bidang, seperti bangun datar, fisika, dan teknik. Oleh karena itu, penting bagi kita untuk memahami rumus ini dengan baik.
Dalam menghitung menggunakan Teorema Phytagoras, kita harus memahami cara menentukan sisi-sisi segitiga siku-siku. Selain itu, kita juga harus memahami tentang sudut-sudut dalam segitiga siku-siku dan bagaimana cara menentukannya menggunakan rumus tangen.
Semoga artikel ini bermanfaat bagi pembaca dalam memahami tentang Rumus Teorema Phytagoras.
