Daftar Isi
Pengertian Rumus Bangun Ruang
Rumus bangun ruang adalah cara untuk menghitung sifat-sifat geometris dari bangun ruang, seperti luas permukaan, volume, dan lain-lain. Rumus ini sangat berguna dalam matematika dan juga dalam kehidupan sehari-hari, terutama dalam industri konstruksi.
Rumus Bangun Ruang Dasar
Beberapa rumus bangun ruang dasar yang sering digunakan adalah sebagai berikut:
Kubus
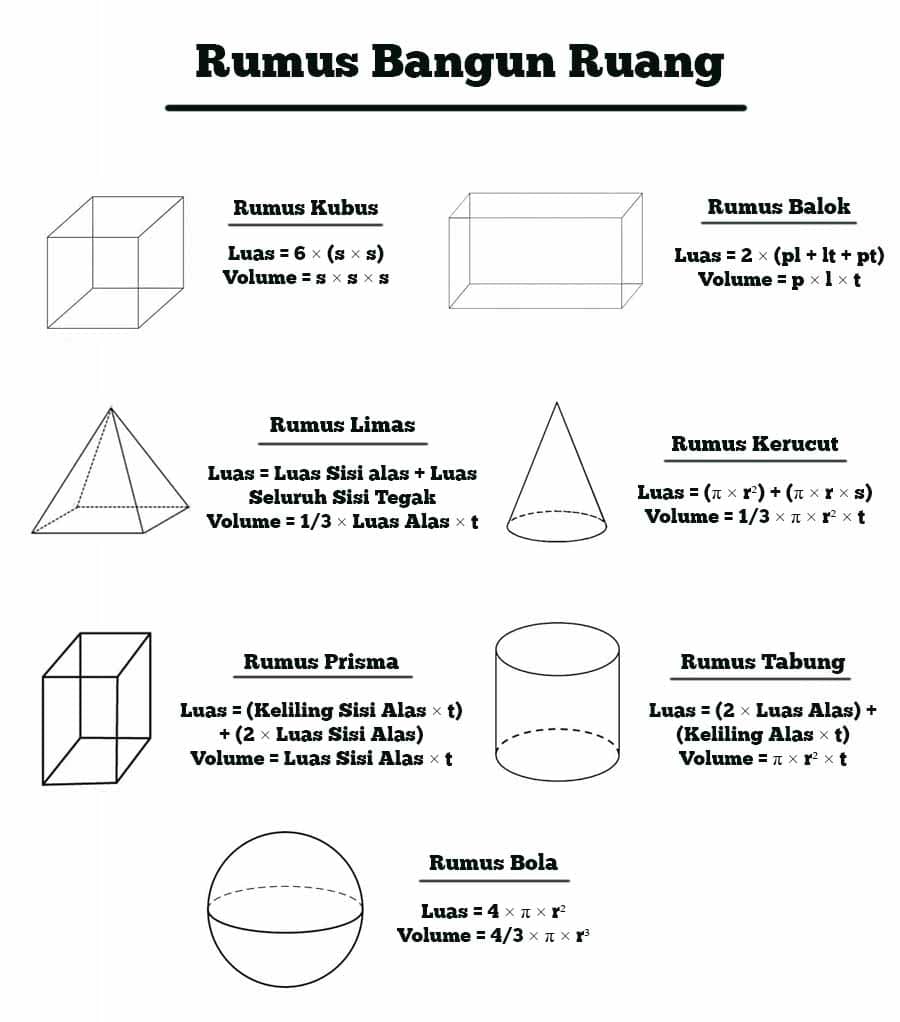
Kubus adalah bangun ruang yang mempunyai 6 sisi yang sama panjang. Rumus-rumus yang digunakan untuk menghitung sifat-sifat kubus adalah sebagai berikut:
– Luas permukaan = 6 x sisi^2
– Volume = sisi^3
Balok
Balok adalah bangun ruang yang mempunyai 6 sisi, 4 sisi berbentuk persegi dan 2 sisi berbentuk persegi panjang. Rumus-rumus yang digunakan untuk menghitung sifat-sifat balok adalah sebagai berikut:
– Luas permukaan = 2 x (panjang x lebar + panjang x tinggi + lebar x tinggi)
– Volume = panjang x lebar x tinggi
Bola
Bola adalah bangun ruang yang mempunyai permukaan yang bulat sempurna. Rumus-rumus yang digunakan untuk menghitung sifat-sifat bola adalah sebagai berikut:
– Luas permukaan = 4 x phi x r^2
– Volume = 4/3 x phi x r^3
Tabung
Tabung adalah bangun ruang yang mempunyai permukaan yang terdiri dari 2 lingkaran dan 1 selimut. Rumus-rumus yang digunakan untuk menghitung sifat-sifat tabung adalah sebagai berikut:
– Luas permukaan = 2 x phi x r x (r + t)
– Volume = phi x r^2 x t
Rumus Bangun Ruang Lainnya
Selain rumus-rumus bangun ruang dasar, terdapat juga rumus-rumus bangun ruang lainnya yang sering digunakan. Berikut adalah beberapa di antaranya:
Limas
Limas adalah bangun ruang yang terdiri dari alas yang berbentuk segi-n dan bidang sisi-sisi yang berbentuk segitiga dengan satu titik tertumpu di atas alas. Rumus-rumus yang digunakan untuk menghitung sifat-sifat limas adalah sebagai berikut:
– Luas permukaan = luas alas + luas selimut
– Volume = 1/3 x luas alas x tinggi
Prisma
Prisma adalah bangun ruang yang terdiri dari dua bidang alas yang sama besar dan sejajar dengan bidang sisi-sisi yang berbentuk segitiga atau segiempat. Rumus-rumus yang digunakan untuk menghitung sifat-sifat prisma adalah sebagai berikut:
– Luas permukaan = 2 x luas alas + luas selimut
– Volume = luas alas x tinggi
Kerucut
Kerucut adalah bangun ruang yang terdiri dari alas lingkaran dan selimut berbentuk kerucut. Rumus-rumus yang digunakan untuk menghitung sifat-sifat kerucut adalah sebagai berikut:
– Luas permukaan = phi x r x (r + s)
– Volume = 1/3 x phi x r^2 x t
Tabung Terpancung
Tabung terpancung adalah bangun ruang yang terdiri dari dua tabung dengan alas dan tinggi yang berbeda. Rumus-rumus yang digunakan untuk menghitung sifat-sifat tabung terpancung adalah sebagai berikut:
– Luas permukaan = 2 x phi x r1 x (r1 + t) + 2 x phi x r2 x (r2 + t)
– Volume = 1/3 x phi x t x (r1^2 + r2^2 + r1 x r2)
Langkah-langkah Menggunakan Rumus Bangun Ruang
Untuk menggunakan rumus bangun ruang, langkah-langkahnya adalah sebagai berikut:
1. Tentukan jenis bangun ruang yang akan dihitung.
2. Tentukan nilai-nilai yang diberikan, seperti sisi, diameter, atau tinggi.
3. Gunakan rumus yang sesuai untuk menghitung sifat-sifat bangun ruang yang diinginkan.
4. Hitunglah nilai sifat-sifat tersebut menggunakan kalkulator.
5. Jangan lupa untuk menyertakan satuan dalam hasil perhitungan.
Contoh:
Sebuah balok memiliki panjang 6 cm, lebar 4 cm, dan tinggi 5 cm. Hitunglah luas permukaan dan volume dari balok tersebut.
1. Jenis bangun ruang yang akan dihitung adalah balok.
2. Nilai-nilai yang diberikan adalah panjang = 6 cm, lebar = 4 cm, dan tinggi = 5 cm.
3. Gunakan rumus untuk menghitung luas permukaan dan volume balok.
– Luas permukaan = 2 x (panjang x lebar + panjang x tinggi + lebar x tinggi)
= 2 x (6 x 4 + 6 x 5 + 4 x 5)
= 2 x (24 + 30 + 20)
= 2 x 74
= 148 cm^2
– Volume = panjang x lebar x tinggi
= 6 x 4 x 5
= 120 cm^3
4. Hitunglah nilai sifat-sifat tersebut menggunakan kalkulator.
5. Jangan lupa untuk menyertakan satuan dalam hasil perhitungan. Jadi, luas permukaan balok tersebut adalah 148 cm^2 dan volumenya adalah 120 cm^3.
Kesimpulan
Rumus bangun ruang sangat penting dalam matematika dan juga dalam kehidupan sehari-hari, terutama dalam industri konstruksi. Ada banyak jenis bangun ruang dan rumus-rumus yang berbeda untuk menghitung sifat-sifat geometrisnya. Untuk menggunakan rumus bangun ruang, perlu dilakukan beberapa langkah seperti menentukan jenis bangun ruang, nilai-nilai yang diberikan, dan rumus yang sesuai. Dengan menggunakan rumus bangun ruang, kita dapat menghitung sifat-sifat geometris dari bangun ruang dengan mudah dan akurat.
 Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
Bicara Fakta Informasi Berita Terkini, Berita Terbaru dan Berita Hari Ini
